数学的旅程往往从简单的开始。

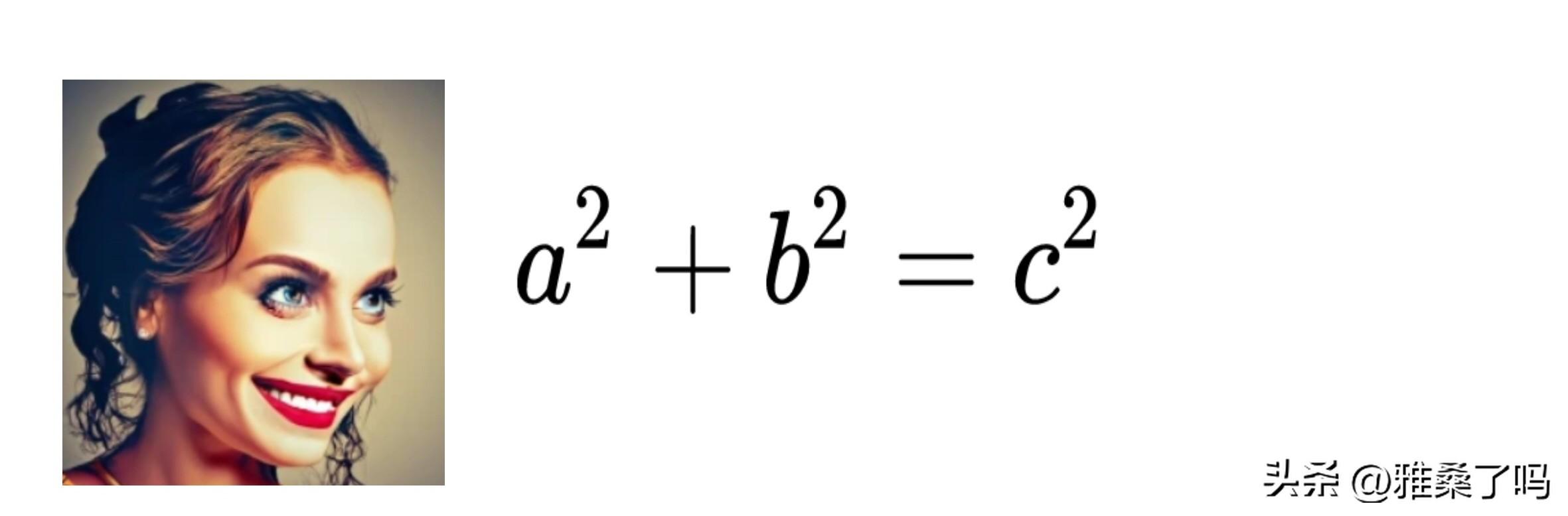
当你第一次接触到勾股定理：a² + b² = c²，你可能会被这个简洁而精巧的公式所吸引。a和b是直角三角形的两条直角边的长度，c是斜边的长度。

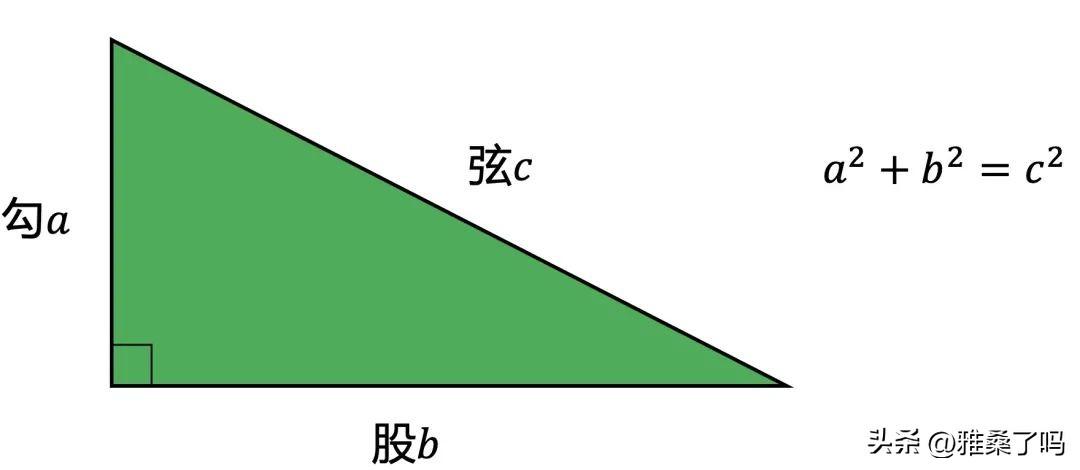
一个实际的应用可能是确定电视尺寸。电视的尺寸通常以屏幕的对角线长度进行测量。如果你知道电视屏幕的宽度（a）和高度（b），你可以使用勾股定理来计算对角线的长度（c），即电视的尺寸。这个新发现带给你的喜悦和兴奋可能是无法言表的，你感觉自己突然对世界有了更深的理解，对未知有了新的认知。

然随着你深入数学的学习，你可能会遇到更复杂、更抽象的公式

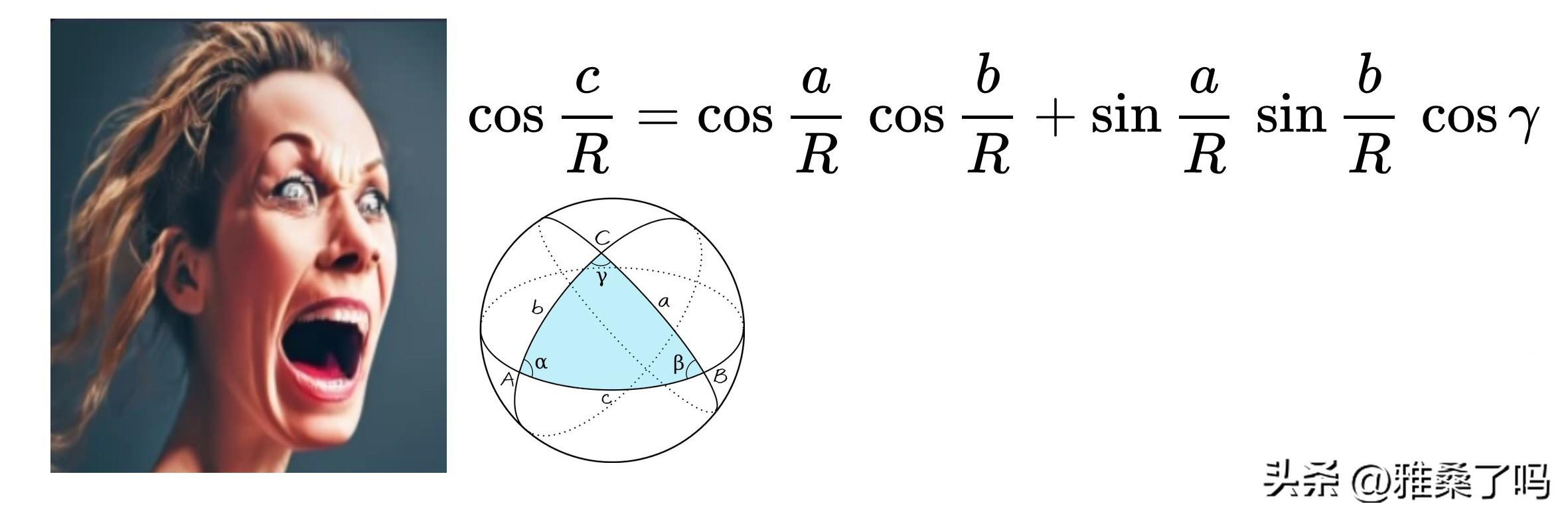
例如球面三角学的公式：cos(c/R) = cos(a/R) * cos(b/R) + sin(a/R) * sin(b/R) * cos(γ)。这个公式看起来比勾股定理复杂得多，而且也没有那么直观易懂。a和b是球面上两点之间的大圆弧长度，c是这两点通过第三点形成的另一条大圆弧长度，γ是这两点在第三点形成的夹角，R是球体的半径。这个公式实际上在很多领域有用，比如航空航天和地理信息系统（GIS）。例如，飞行员或航海员可能需要用此公式来计算地球上两点之间的最短路径（大圆航线），这是因为地球是一个大球体，又或者是计算星星在天空中的位置，等等。所以传统的平面几何学不能给出准确的答案。

你需要理解三角函数，理解球体几何，理解角度和半径的关系。所有这些元素融合在一起，形成了一个你需要攻克的难题。可能在这个过程中，你会感到疯狂，感到迷惑，甚至有些失落。

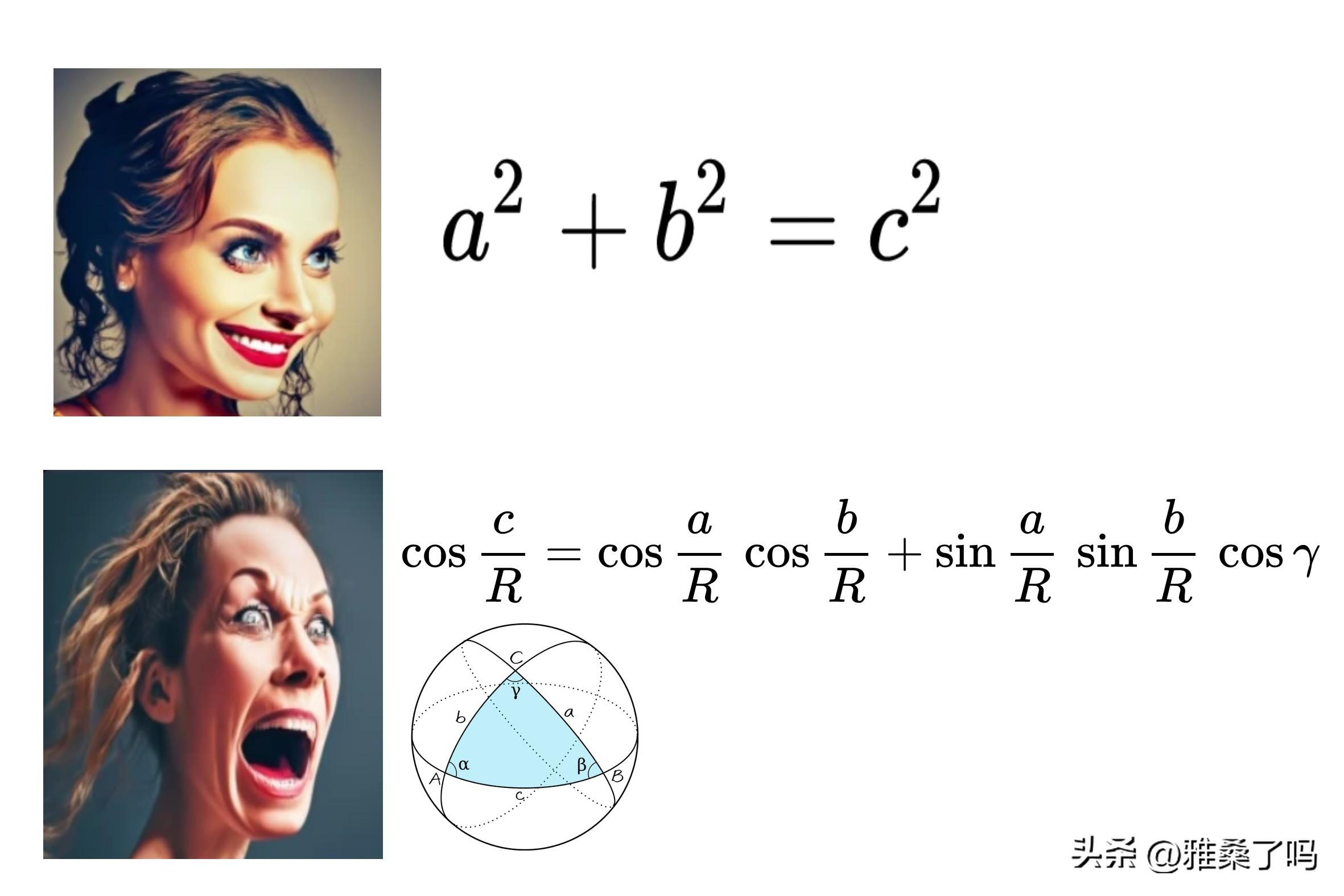
从勾股定理的欢乐，到球面三角学的疯狂，这就是数学的魅力。在探索未知的过程中，我们可能会感到困惑，甚至疯狂。但是，每当我们攻克一个难题，理解一个新概念时，我们都会体验到数学的乐趣，体验到新知识的兴奋。所以，让我们欣然接受这个充满欢乐与疯狂的数学旅程，享受其中的每一刻。