自17世纪近代数学产生以来，函数的概念一直处于数学的核心位置，数学和科学的绝大部分与函数的内容有关，在数学、物理和其他学科中，函数关系随处可见。例如，圆柱体的体积和表面积是其半径的函数，流体膨胀的体积是温度的函数，运动物体的路程是时间的函数等等。

马克思曾认为，函数概念是源于代数中自罗马时代就已经开始的不 定方程的研究，那时，伟大的数学家丢番图对不定方程的研究已有相当程度，据此，可以认为函数概念至少在那时已经萌芽。实际上作为变量和函数的朴素概念，几乎和数学源于同一时期，因为数学家在研究物体的大小及位置关系时，自然会导致通常称为函数关系的那种从属关系。但是，真正导致函数概念得以迅速发展则是在16世纪以后，特别是由于微积分的建立，伴随这一学科的产生、发展和完善，函数概念也经历了产生、发展和完善的演变过程。

哥白尼的天文学革命以后，运动成为文艺复兴时期科学家共同感兴趣的问题，到了16世纪，对于运动的研究已变成自然科学的中心问题。在这一时期，函数概念在不同科学家那里有着不同形式的描述。

十七世纪，伽俐略（G．Galileo，意，1564－1642）在《两门新科学》一书中，几乎从头到尾包含着函数或称为变量的关系这一概念，用文字和比例的语言表述函数的关系。例如，他提出：“两个等体积圆柱体的面积之比，等于它们高度之比的平方根。”“两个侧面积相等的正圆柱，其体积之比等于它们高度之比的反比。”他又说：“从静止状态开始以定常加速度下降的物体，其经过的距离与所用时间的平方成正比。”这些描述非常清楚地表明伽利略已涉及并讨论变量和函数，但他并没有做出一般的抽象，并且也没有把文字叙述表示为符号形式。

笛卡尔（Descartes，法，1596－1650）在他的解析几何中，已经注意到了一个变量对于另一个变量的依赖关系，但由于当时尚未意识到需要提炼一般的函数概念，因此直到17世纪后期牛顿、莱布尼兹建立微积分的时候，数学家还没有明确函数的一般意义，绝大部分函数是被当作曲线来研究的。

牛顿在创立微积分的过程中一直用“流量”一词来表示变量之间的依赖关系，并且从运动的角度，把曲线看成是动点的轨迹。他在《求曲边形的面积》中说：“我认为这里的数学量，不是由小块合成的，而是由连续运动描出的，线（曲线）是描画出来的，因而它的产生不是由于凑零为整，而是由于点的连续运动……”

“函数”作为数学术语是由微积分的另一位创立者莱布尼兹于1673年引进的，他用“函数”一词表示任一个随着曲线上的点变动的量,并指出：“像曲线上点的横坐标、纵坐标、切线的长度、垂线的长度等，所有与曲线上的点有关的量称为函数。”除此以外，他还引进了“常量”、“变量”和“参变量”等概念，一直沿用到现在，这个定义仅是在几何范围内揭示某些量之间所存在的依赖关系，并未给出函数的解析定义，因此，莱布尼兹所给出的函数的定义可看成是“函数概念的几何起源"。

1718年，约翰•贝努利（BernoulliJohann，瑞，1667－1748）才在莱布尼兹函数概念的基础上，对函数概念进行了明确定义：由任一变量和常数的任一形式所构成的量，贝努利把变量x和常量按任何方式构成的量叫“x的函数”，表示为f(x)，其在函数概念中所说的任一形式，包括代数式子和超越式子。

18世纪中叶，欧拉（L．Euler，瑞，1707－1783）就给出了非常形象的，一直沿用至今的函数定义。欧拉给出的定义是：一个变量的函数是由这个变量和一些数即常数以任何方式组成的解析表达式。这就把变量与常量以及由它们的加、减、乘、除、乘方、开方和三角、指数、对数等运算构成的式子，均称为函数。并且，欧拉把约翰•贝努利给出的函数定义称为解析函数，并进一步把它区分为代数函数（只有自变量间的代数运算）和超越函数（三角函数、对数函数以及变量的无理数幂所表示的函数），还考虑了“随意函数”（表示任意画出曲线的函数），不难看出，欧拉给出的函数定义比约翰•贝努利的定义更普遍、更具有广泛意义。

1822年，法国数学家傅立叶（Fourier，法，1768－1830）提出了任意函数可展开为三角级数，这实际上是说，不管是连续函数或不能用解析表达式给出的函数（凡能用图形给出）都可以用三角级数表示．因此也说明了，仅从表达式是否“单一”，或函数是否连续来区别是不是函数，显然是不合理的。

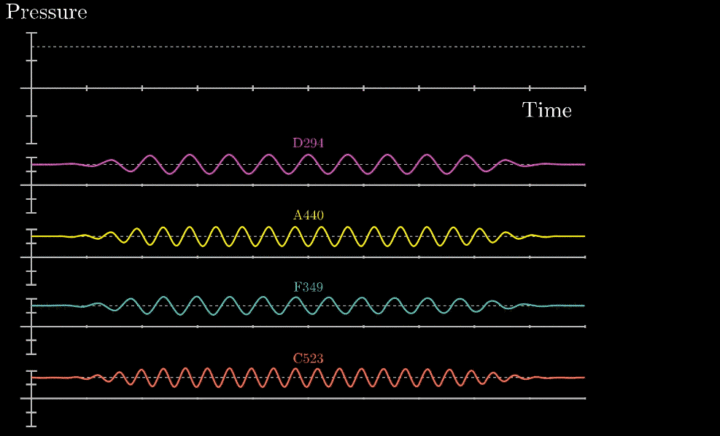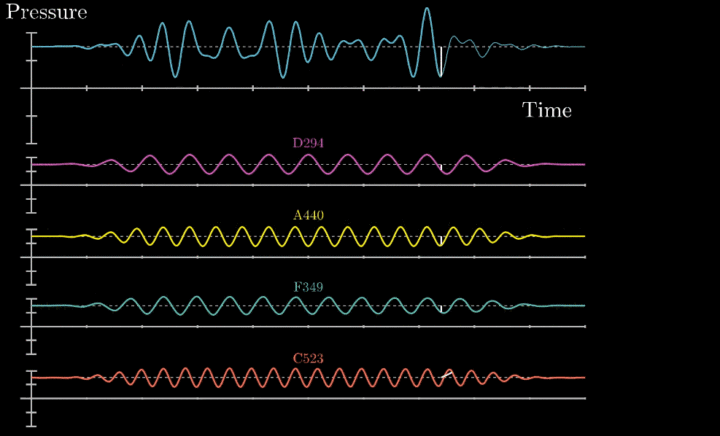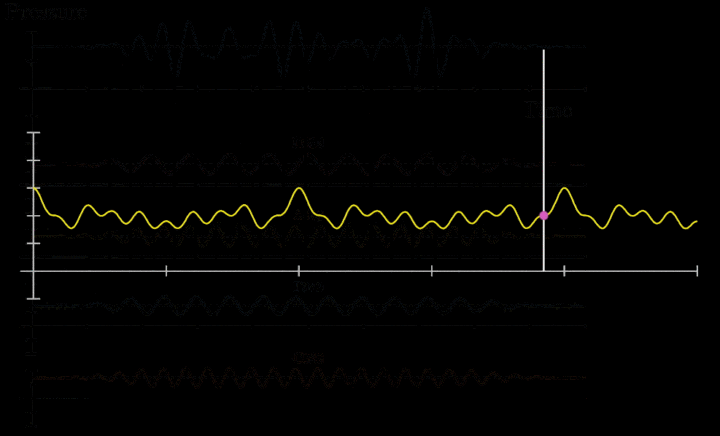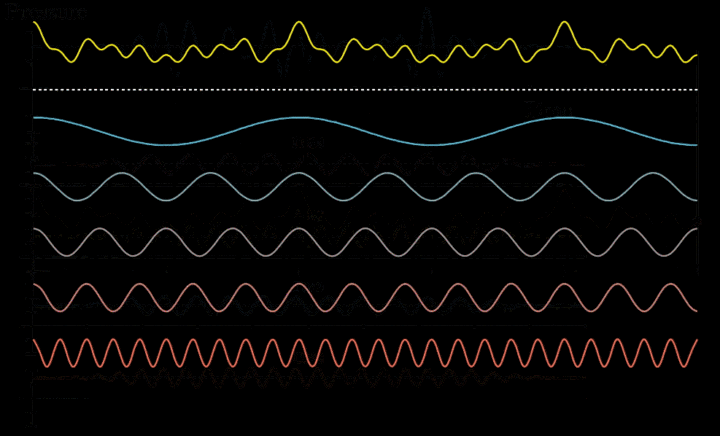
傅立叶在论文《热的分析理论》中，证明了“由不连续的线给出的函数，能用一个三角函数式来表示”。他举例指出某些不连续曲线，表达式有无穷多个，例如：

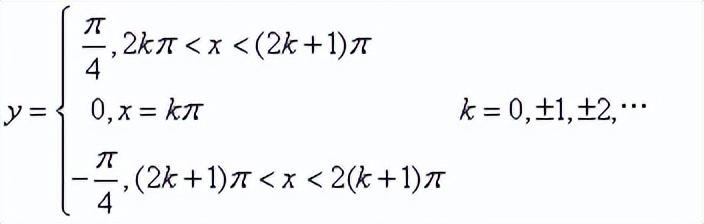
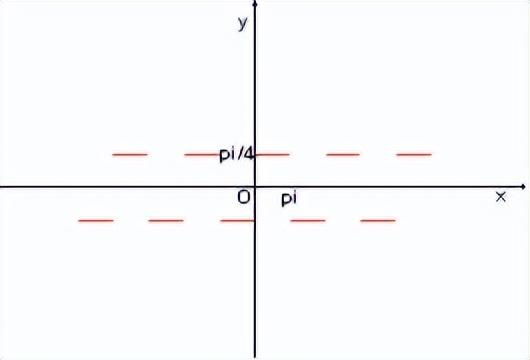
但可以用单一的三角式表示为：

这有力地揭示了，用函数表示式的“单一”与否来区别函数的真伪是不行的，不久人们进一步发现了同一曲线即可用同一个函数，也可用两个以上的函数表示的种种例子，从而结束了函数概念是否以唯一一个式子表示的争论，把对函数的认识又推进了一个新的层次。

1823年，柯西（Cauchy，法，1789－1857）从定义变量开始给出了函数的定义，同时指出，虽然无穷级数是规定函数的一种有效方法，但是对函数来说不一定要有解析表达式，不过他仍然认为函数关系可以用多个解析式来表示，这是一个很大的局限，突破这一局限的是杰出数学家狄利克雷。

1837年，狄利克雷（Dirichlet，德，1805－1859）认为怎样去建立x与y之间的关系无关紧要，他拓广了函数概念，指出：“对于在某区间上的每一个确定的x值，y都有一个或多个确定的值，那么y叫做x的函数。”狄利克雷的函数定义，出色地避免了以往函数定义中所有的关于依赖关系的描述，简明精确，以完全清晰的方式为所有数学家无条件地接受。至此，我们已可以说，函数概念、函数的本质定义已经形成，这就是人们常说的经典函数定义。

随后的斯铎克斯、罗巴切夫斯基、黎曼等都分别给出了函数的定义。

例如，黎曼于1851年给出这样一个定义：

我们假定z是一个变量，它可以逐次取所有可能的实数值。若对它的每个值都有未定量w的唯一的一个值与之对应，则w称为y的函数.

黎曼指出，这个定义完全没有规定在单个的函数值之间存在一种规律，此时，如果函数在某个区间已有定义，它在该区间外的延拓方式是完全任意的，人们所定义的量w对量z的依赖关系是任意给定的或是由量的某种运算所确定并没有什么差异。

总之，从18世纪前后开始，经过许多数学家的不断探索和研究，函数概念有了长足的发展。但至少到19世纪前半期，关于函数概念的叙述仍是不一致的，比如，当时一些最好的教科书，有的沿用18世纪函数解析式的定义，有的利用近似黎曼的定义等等。因此函数的概念仍需进一步完善。

在分析严格化的过程中，集合论的思想逐渐形成。皮亚诺发表了《无穷悖论》，标志着他是第一个朝着建立集合的明确理论的方向迈出积极步伐的人。

等到康托尔（Cantor，德，1845－1918）创立的集合论在数学中占有重要地位之后，维布伦（Veblen，美，1880－1960）用“集合”和“对应”的概念给出了近代函数定义，通过集合概念，把函数的对应关系、定义域及值域进一步具体化了，且打破了“变量是数”的极限，变量可以是数，也可以是其它对象（点、线、面、体、向量、矩阵等）。

1914年豪斯道夫（F．Hausdorff）在《集合论纲要》中用“序偶”来定义函数，其优点是避开了意义不明确的“变量”、“对应”概念，其不足之处是又引入了不明确的概念“序偶”。库拉托夫斯基（Kuratowski）于1921年用集合概念来定义“序偶”，即序偶(a，b)为集合{{a}，{b}}，这样，就使豪斯道夫的定义很严谨了。1930年，新的现代函数定义为，若对集合M的任意元素x，总有集合N的确定的元素y与之对应，则称在集合M上定义一个函数，记为y=f(x).元素x称为自变元，元素y称为因变元。

函数概念通过两百多年的锤炼，变革，形成了函数现代定义，应该说已经相当完善了，不过数学的发展是无止境的。函数现代定义的形式并不意味着函数概念发展的历史终结，近几十年来，数学家们又把函数归结为一种更广泛的概念——“关系”。

目前，使用较多的定义有如下两种：

【定义1】 设在某个变化过程中有两个变量x，y，如果对于x在某一范围内的每一个确定的值，y都有唯一确定的值与之对应，就说y是x的函数，x叫做自变量。

这个定义揭示了函数概念的本质，明确了函数的三要素，易被初学者接受和理解，我国初中教材采用这种定义。

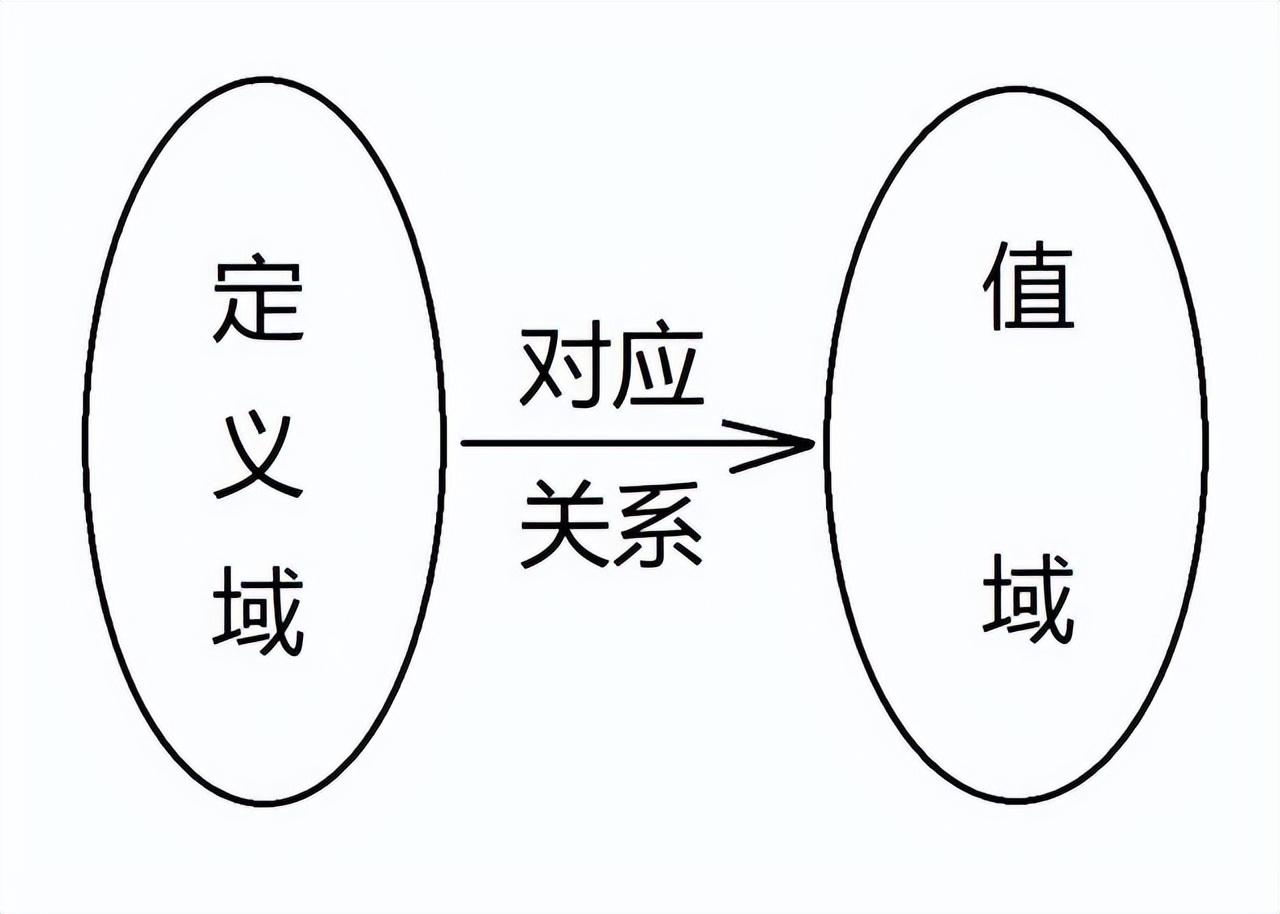
【定义2】 设A、B是两个非空数集，如果按照某种确定的对应法则f，对于A中的任一个元素，在集合B中都有唯一确定的元素f(x)与之对应，这样的对应f叫做从集合A到集合B的一个函数，记为f：A→B，也可记做y=f(x)。

这个定义指出了函数的三要素：定义域、对应法则、值域。由于它是在集合与对应的基础上给出的，故又称“对应说”或“映射说”，高中教材采用这种定义。

总的来说，函数的定义大致经历了这样几个阶段：把研究的曲线当作函数；把由一个变量和一些常量以任何方式形成的解析表达式作为函数；用对应关系定义的函数；用集合定义的函数。或者另外一种说法是：函数概念从变量说发展到对应说，又从对应说进一步完善到现在的关系说。

但是，随着数学的横向和纵向发展，函数概念到此还没有终结，还在发展。分析函数概念的形成历史，我们可以看出几点：首先，函数概念的形成是由研究静止现象到研究运动、变化现象的结果。其次，函数概念的形成是人类活动不断深化的结果，是人类思维能力和认识能力提高的结果。