对数与对数函数是高中数学的重要知识点，也是高考的必考点。本文和大家分享一道1990年高考文史类数学真题，题目就是解对数不等式，难度不算大。曾经将这道题目拿给高一学生做，他们表示真的很简单，不少同学直言能得满分。那么接下来我们一起来看看这道高考真题。

题目见上图。这是一道典型的解对数不等式的题目，而对数不等式的常见类型分为两大类：一类是底数已经确定的对数不等式；另一类是底数不确定，即底数含有参数的对数不等式。

第一类底数确定的对数不等式又可以分为底数相同和底数不同的两类。底数相同时直接根据对应对数函数的单调性求解即可，底数不同时首先需要根据对数的计算法则变换为底数相同的形式，再按照底数相同的方法求解。

第二类底数含有参数的对数不等式就需要对参数进行分类讨论。分类讨论的依据就是底数在0到1、大于1两种情况。

在做这道题之前，我们先来看两道比较简单的对数不等式。

第一题：

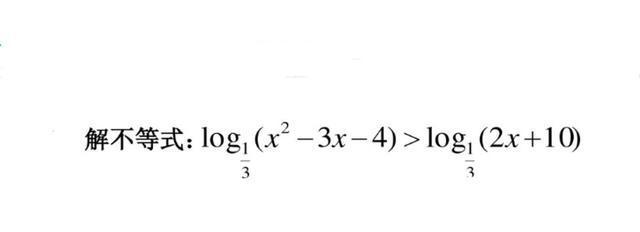
这道题就是一道简单的已知底数的对数不等式，要解这道题就要用到对数函数的单调性。

因为底数1/3是大于0而小于1的，所以对应的对数函数是减函数，那么就可以将函数值大小的比较变为真数大小的比较，即x^2-3x-4＜2x 10。

不过，需要特别注意的是，对数的真数部分必须大于零，所以还有两个关系，即：x^2-3x-4＞0，2x 10＞0。这样就构成了一个不等式组，解出这个不等式组就可以得到答案。

第二题：

这道题目中对数的底数含有参数a，所以基本思路就是讨论参数的取值范围。但是题目中已经告诉了不等式的一个解，那么可以先通过这个解找出a的范围，这样就可以避免讨论。

将x=3代入原不等式，分析可得：a＞1，所以对应的对数函数为增函数，那么可以得到：x^2-x-2＜3x 3，x^2-x-2＞0，3x 3＞0，解出即可。

再回到这道高考题。这也是一道底数含参数的对数不等式，而且没有条件可以确定参数a是在大于零小于1还是大于1的范围，所以需要进行分类讨论。

首先将左边减号后的式子移到右边，再根据对数加法的法则进行处理。处理后再进行分类讨论。

①当0＜a＜1时，对应的对数函数是减函数，函数值大的真数反而小，即：

4 3x-x^2＜2(2x-1)。且各自的真数都要大于零，即：4 3x-x^2＞0，2(2x-1)＞0。解出这个不等式组即可。

②当a＞1时，对应的对数函数是增函数，此时函数值大的真数也大，所以：

4 3x-x^2＞2(2x-1)。再加上真数大于零又可以构成一个不等式组，解出即可。

这道高考真题位于当年解答题的第四题，整体来说难度不大。不过还是有不少同学容易忽略真数大于零这样一个隐含的限制条件而导致答案出错。如果是你，这道题你能得满分吗？