作品编号:022
投稿时间:2020.7.28
一、教学目标
1、学生在具体的生活情境中发现问题,产生疑惑从而开始新知识的探索,养成良好地独立思考和探究未知的行为习惯。
2、用数格子(或割、补、拼等)的办法和“几何画板”操作法体验勾股定理的探索过程,并能由此猜想出勾股定理,培养学生的探索精神。
3、在教师的引导下,学生探索用“赵爽弦图证法”和“总统证法”证明勾股定理,学生经历“观察—猜想(操作)—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法。
4、深刻理解勾股定理的内涵,并能运用勾股定理进行简单的计算,解决相关实际问题.
5、学生在中西方勾股定理的发展和证明历史长河中,品味数学文化,感受数学魅力。
二、教学重难点
重点:了解勾股定理的验证的思想方法,体会数形结合和特殊到一般的思想方法。
难点:理解勾股定理的内涵。
三、教学过程
(一)创设情境,导入新课
以观看台风的实况录像,提出问题:受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处(如图1),这棵树折断前有多高?
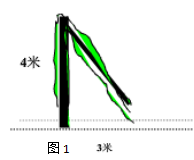
设计意图:目的是激发学生的探究欲望,教师引导学生将实际问题转化成数学问题,也就是“已知一直角三角形的两边,如何求第三边?” 的问题。学生会感到困难,从而教师指出学习了今天这一课后就可以解决了,同时又对其进行抗台风精神的宣扬。
(二)动手操作,探索新知
【活动1】 毕达哥拉斯发现了什么?
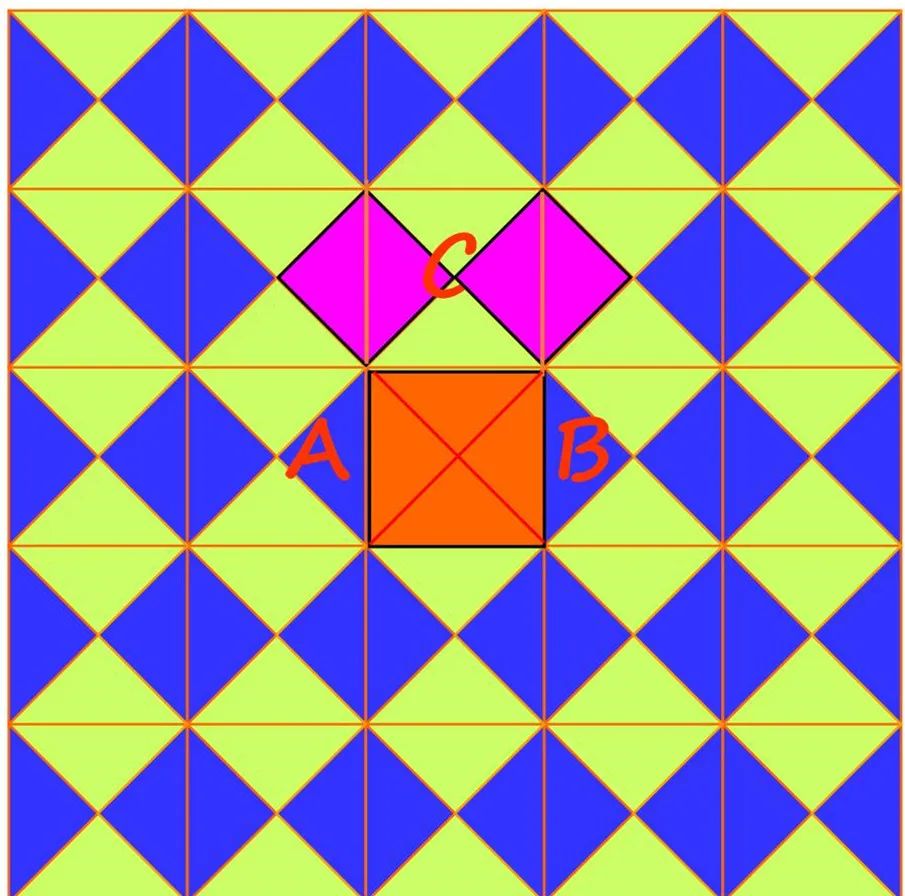
2500年前,古希腊著名的哲学家、数学家、天文学家毕达哥拉斯有一次在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形三边的种数量关系。我们也来观察下面图1中的地面,看看能否发现些什么?

图二
探究活动1:学生自主探索,组内交流,总结发现的结论,最后进行展示。教师根据发现的结论,提炼出直角三角形的三边的关系,为探究活动2做好铺垫。
图三
探究活动2:你能用图3证明等腰Rt△ABC的三边长之间所满足的等量关系吗?
教师总结:两个红色的小正方形可以看成四个全等的小三角形,刚好可以拼接成桔黄色的大正方形,及两个小正方形面积和等于大正方形面积。
即得结论:等腰直角三角形中,两条直角边的平方和等于斜边的平方。
设计意图:通过再现历史,让学生在历史的长河中感觉勾股定理的产生过程,明白数学知识来源于生活,培养学生在生活中探索知识的良好习惯。
【活动2】 用“几何画板”探索一般直角三角形三边之间的关系
请同学们注意观察下面的操作演示,你能得到什么结论?
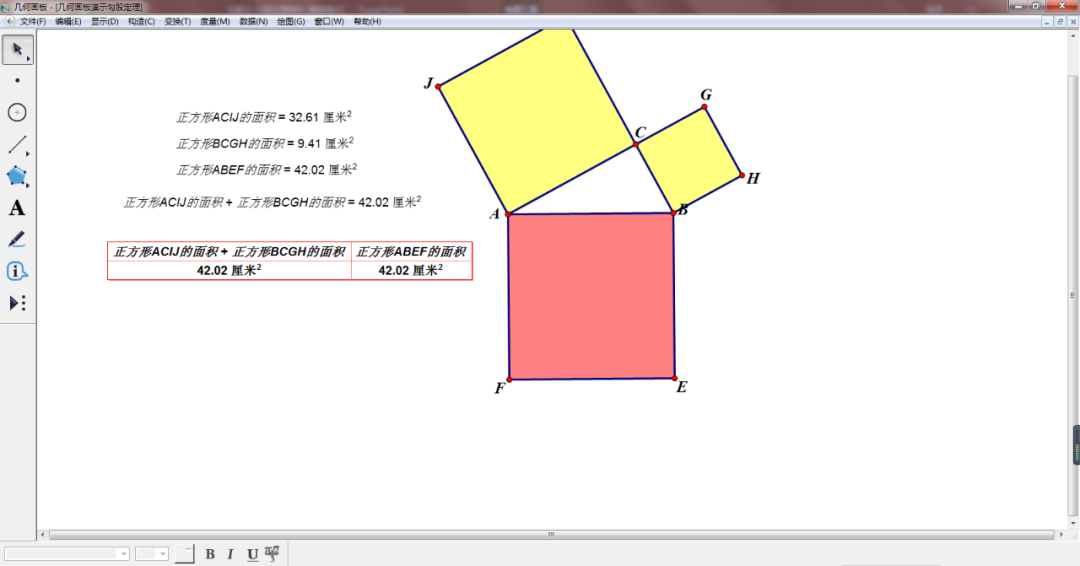
探究活动:
1、改变直角三角形的两条直角边,你发现哪些量改变,哪些量不变?
2、如果改变直角三角形的三条边的长度都改变,结果又是怎样的?
【猜想】根据以上2个探索活动,我们可以猜想:
命题1:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么
设计意图:通过几何画板的演示,直观展示直角三角形三边的关系,进一步验证活动1的结论,培养学生数形结合思想。
【历史再现】
在古汉语里,人们将手臂弯曲成直角(如图4),上半部分称为“勾”,下半部分称为“股”。在直角三角形中,一般的我们把“较短的直角边叫勾, 较长的直角边叫股,斜边叫弦”。

人们对勾股定理的认识经历了从特殊到一般的过程。最早发现“勾三股四弦五”这一特殊关系的是大禹治水时期,而有历史记载的是奴隶社会时期的商高,据《周髀算经》记载:商高曾对周公说:“故折矩,勾广三,股修四,经隅五。”也就是我们现在所说的“勾三股四弦五”。勾股定理名称也就来源于此。古埃及也独立的发现了这一关系,据历史考证金字塔下面底座的直角就是利用它建造的。在西方,最早发现勾股定理的是古希腊的毕达哥拉斯,他发现了勾股定理的一般形式,还为此杀了一百头牛来庆贺。因此在西方被称为“毕达哥拉斯定理”或是“百牛定理”。勾股定理的应用非常的广泛,古自大禹治水,陈子测日,近到宇宙探索它都起了巨大的作用。
设计意图:了解中西方关于勾股定理历史,感受数学之美,了解勾股定理在数学中的价值。
(三)中西对比,证明定理
引言:勾股定理的证明也吸引了无数的数学家和数学爱好者。几千年来人们已经发现了五百多种证明的方法,足以编成厚厚的一本书。因此,勾股定理也可以称为“千古第一定理”。下面我们一起来探讨我国古代的“赵爽弦图证法”和“美国第二十任总统伽菲尔德的总统证法”
【赵爽弦图证法】
汉时(约公元222年),赵独创了一种叫做“弦图”的图形(如图5),这是用两个全等的直角三角形(三角形涂上了朱色,它的面积称为“朱实”,图5中的ACBD部分)全成一个矩形,再用这样的四个矩形合成一个空心正方形,中间的空心部分涂上黄色,它的面积叫“中黄实”,又叫“差实”。以弦为边的正方形ABEF叫“弦实”.四个朱实加上一个黄实就等于一个弦实。
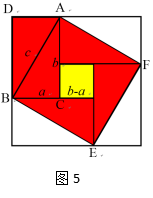
探究活动:1、图中有几个直角三角形?每一个直角三角形的面积如何表示?
2、中间小正方形(黄色的正方形)的面积如何表示?
3、你能用几种方法表示正方形ABEF的面积?
证法梳理:每一个直角三角形的面积为,中间小正方形的面积为
正方形ABEF的面积可能表示为4个全等的直角三角形的面积与中间小正方形的面积之和,即为,又可以表示为.
所以有.化简后得.
方法引领:赵爽弦图证法,通过割补拼接巧妙地构造几何图形,用两种不同的方法表示同一个正方形的面积,从而得出直角三角形三边的关系,该方法也叫做面积法。在该过程中至少蕴含两种的数学思想方法,其一是数形结合思想,其二是方程的思想.
【总统证法】
伽菲尔德(1831-1881年),美国第二十任总统。在他任众议院议员时,曾发表一种简单的证明勾股定理的方法,后来将这种方法称为总统证法。如图6,以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.

探究活动:同学们,你们能根据赵爽弦图证明的思维方法完成勾股定理的证明吗?
证法梳理:∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90º,
∴ ∠AED + ∠BEC = 90º.
∴ ∠DEC = 180º―90º= 90º.
∴ ΔDEC是一个等腰直角三角形,它的面积等于.
又∵ ∠DAE = 90º, ∠EBC = 90º,
∴ AD//BC. ∴ ABCD是一个直角梯形,它的面积等于.
∴. ∴.
【总结提升】
勾股定理:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么
探究活动:1、勾股定理的使用条件?
2、勾股定理可以用来解决什么问题?
教师总结:1、只适用于直角三角形,而一般的三角形不一定适用。
2、勾股定理是解决已知直角三角形的两边,求第三边的问题。其变形公式如
下:
设计意图:通过探究中西方两种证明勾股定理的方法,在对比中感受两种文化的差异和相似之处,培养学生严谨的治学态度,进一步培养学生的数形结合思想。
(四)应用知识,回归生活
例1 已知在Rt△ABC中,a、b为直角边,c为斜边,根据下列已知条件求值:
(1)a=6,c=10, 则 b= .
(2)a=5,b=12,则 c= .
(3)a=1, b=1,则 c= .
(4)在直角三角形中有一边为3,一边为4,另一边是 .
探究活动: 学生自主完成解答,完成后可以组内交流。最后学生展示解答过程和答案。
设计意图:通过学生自主完成该例题,学会运用勾股定理解决相关问题,达到巩固知识的目的。
例2 导入新课时,我们提出了一个问题,同学们现在能解决吗?问题:受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
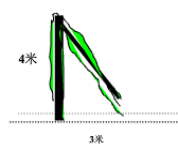
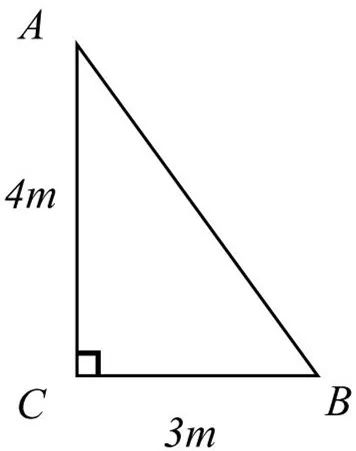
设计意图:解决导入时候提出的问题。前后呼应,学生从中体会到数学来源于生活同时又回归生活,为生活服务。在解决问题时,引导学生如何将实际问题抽象为数学问题,从而实现用数学知识解决实际问题。
(五)图片欣赏,梳理总结
【图片欣赏】




设计意图:通过图片欣赏,感受数学之美,感爱勾股定理之美,培养学生热爱数学和探索数学的精神。
【梳理总结】
1、直角三角形三边有怎样的数量关系?勾股定理主要用于解决什么问题?
2、你是怎样理解勾股定理称为“千古第一定理”的?
3、本节课的学习你参与讨论吗?新知识的学习你检测的结果如何?
(六)布置作业,拓展思考
【作业】 1、课本P70 2、3、7
2、预习课本P66-67。思考课本中的探究。
【拓展】印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题。





发表评论