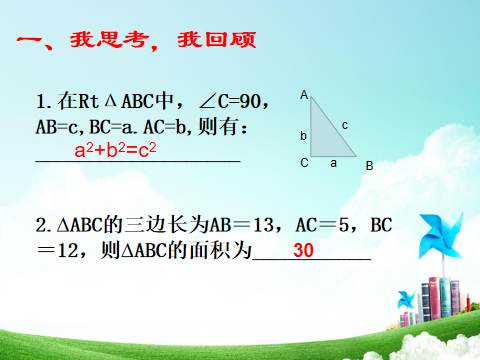
知识点：

勾股定理在网格中的应用

例1已知正方形的边长为1，(1)如图a，可以计算出正方形的对角线长为根号2.

①分别求出图(b)，(c)，(d)中对角线的长

②九个小正方形排成一排，对角线的长度

(用含n的式子表示)为（ ）

分析：借助于网格，构造直角三角形，直接利用勾股定理.

勾般定理在最短距离中的应用

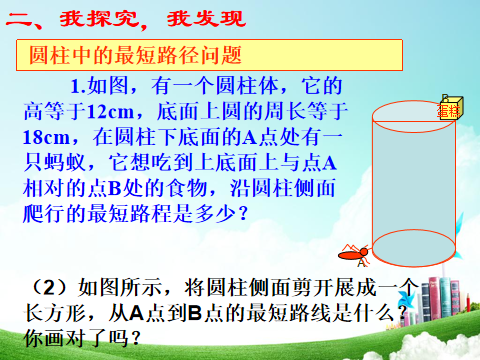
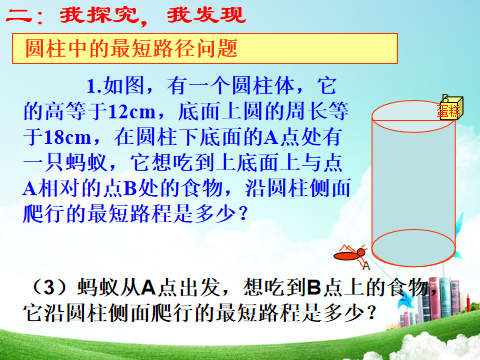
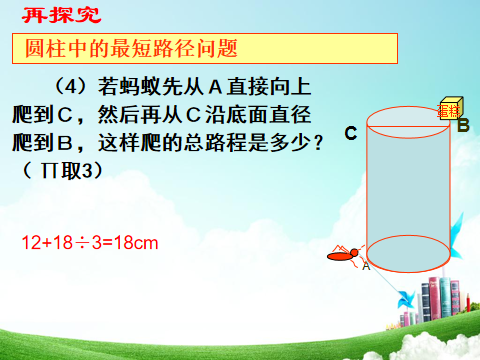
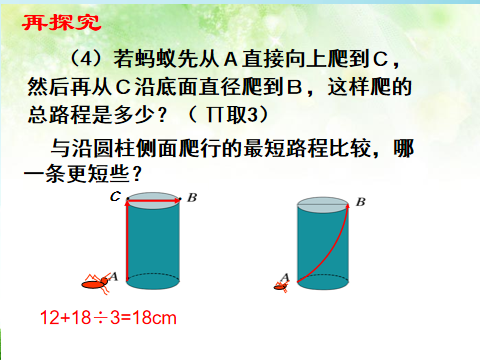
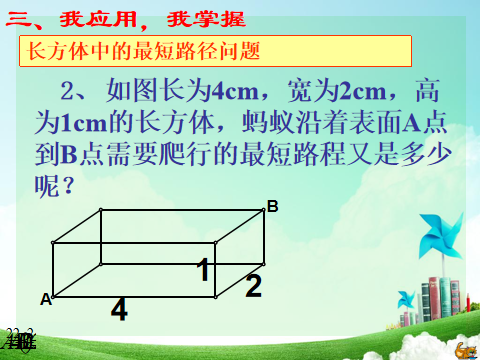
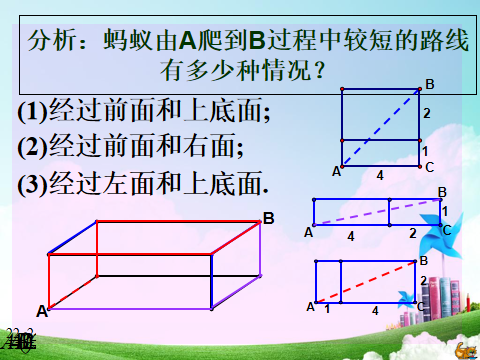
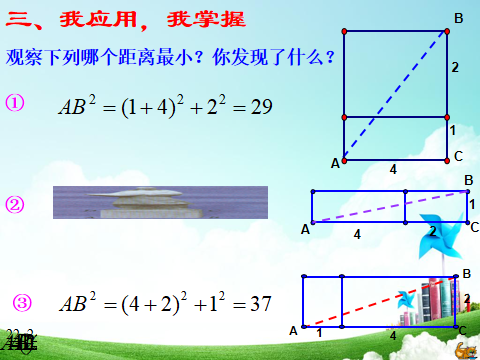
例2 如图，已知C是SB的中点，圆锥的母线长为10cm，侧面展开图是一个半圆，A处有一只蜗牛想吃到C处的食物，它只能沿圆锥曲面爬行.请你求出蜗牛爬行的最短路程.

分析 在求解几何图形两点间最短距离的问题时，将几何体表面展开，求展开图中两点之间的距离，展开过程中必须要弄清楚所要求的是哪两点之间的距离，以及它们在展开图中的相应位置.

勾股定理在生活中的应用

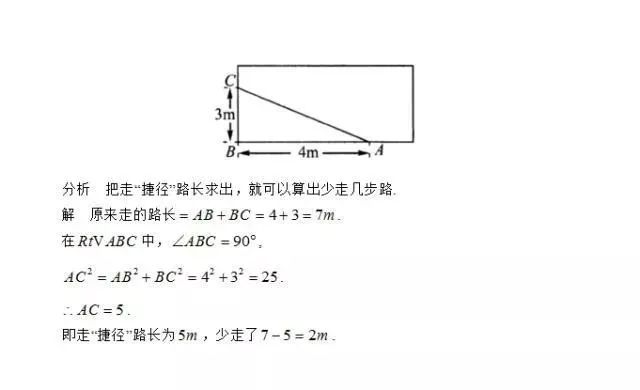
例3 如图，学校有一块长方形花园，有较少数同学为了避开拐角走“捷径”，在校园内走出了一条“路”.请同学们算一算，其实这些同学仅仅少走多少步路，却踩伤了花草.(假设1步为0.5m)

例4 小华想知道自家门前小河的宽度，于是按以下办法测出了如下数据:小华在河岸边选取点A，在点A的对岸选取一个参照点C，测得∠CAD=30°，小华沿河岸向前走30m选取点B，并测得∠CBD=60°.请根据以上数据，用你所学的数学知识，帮小华计算小河的宽度.

视频教学：

练习：

1.如图是一个底面为等边三角形的三棱柱，在三棱柱的侧面外部，从顶点A到顶点

镶有一圈金属丝.已知此三棱柱的高是5cm，底面边长是4cm，则这圈金属丝的长度至少为()

A.8 cmB.13 cmC.12 cmD.15 cm

2.我国南宋著名数学家秦九韶的著作《数书九章》里记载了这样一道题目:“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是:有一块三角形沙田，三边长分别为5里，12里，13里，问这块沙田面积有多大？题中的“里”是我国市制长度单位，1里=500米，则该沙田的面积为()

A.7.5平方千米B.15平方千米C.75平方千米D.750平方千米

3.如图，在一个高是5m，长是13m的楼梯表面铺地毯，则地毯的长度至少是()

A.13mB.17mC.18mD.25m

4.如图是一个三级台阶，它的每一级的长、宽、高分别为5cm，3cm，1cm，A和B是这个台阶相对的点，点A处的一只蚂蚁想到点B处去吃可口的食物，则这只蚂蚁从点A出发，沿着台阶面爬到点B的最短路径长是()

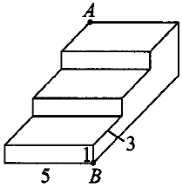
A.12 cmB.13 cmC.14 cmD.15 cm

5.《九章算术》是我国古代一部著名的数学专著，其中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？其意思如下：有一根与地面垂直且高一丈的竹子（1丈=10尺），现被大风折断成两截，尖端落在地面上，竹尖与竹根的距离为三尺，问折断处高地面的距离为()

A.5.45尺B.4.55尺C.5.8尺D.4.2尺

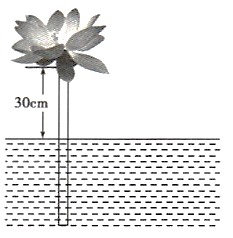
6.如图，在波平如镜的湖面上，有一朵盛开的美丽的红莲，它高出水面30cm.突然一阵大风吹过，红莲被吹至一边，花朵下部刚好齐及水面，如果知道红莲移动的水平距离为60cm，那么水深是()

课件：

教案：

周次

课 型

复习课

主备人

课题

3.3勾股定理的应用举例

教学目标

知识与技能目标：

将实际问题抽象成数学问题，利用数学中的建模思想构造直角三角形，会用勾股定理解决实际问题；已知直角三角形一条边的长和另外两条边的关系，能用勾股定理列出方程。

能力与情感目标：培养学生的观察能力、动手能力自学能力、计算能力、逻辑思维能力；通过运用勾股定理知识解决具体问题，提高分析能力和观察能力。

数学思考：在利用勾股定理解决实际问题的过程中，体验数学学习的实用性．经历将实际问题抽象成数学问题的过程，在操作、观察、分析过程中培养学生主动探究的习惯。

教学重点

勾股定理的应用。

教学难点

将实际问题转化为数学问题。

教具准备

导学过程

二次备课

一、巧设问题，引入课题：

“大家喜欢旅游吗？”与学生的对话激发学生对勾股定理的应用探知的需求！本节课带领学生到烟台的一座小城去游玩，由第一站护城河引出芦苇题，第二站到博物馆引出旗杆练习题，第三站到美食一条街引出汽车过单行道拱门的题。小热身砸金蛋游戏环节复习常见的勾股数：10以内数字打头的勾股数你知道有谁吗？夯实基础，为应用题的计算快捷提供依据。

二、新知学习：

1、第一站：

河边上有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向

岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?

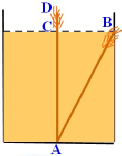
解：设水池的水深AC为x尺，则这根芦苇长为

AD=AB=（x+1）尺，在直角三角形ABC中，BC=5尺.

由勾股定理得:BC2+AC2=AB2.

即52+x2=（x+1）2.

25+x2=x2+2x+1.

2x=24.

∴x=12，x+1=13．

答：水池的水深12尺，这根芦苇长13尺．

2、第二站：(学生自做，计时5分钟竞赛)

你想知道博物馆旗杆的高度，而又不能把旗杆放倒测量，当地工作人员发现旗杆顶端的绳子垂到地面还多2米，当他们把绳子下端拉开8米后，绳子刚好斜着拉直下端接触地面，你能算算旗杆的高度吗?

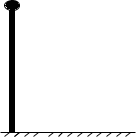
3、第三站：

美食街是个单行车道，你乘坐的车要通过一个拱门，此拱门的截面是一个半径为3.9m的半圆形，你乘坐的车高3.5m、宽3m，你能顺利通过该拱门吗？

（本环节是教学重点：1、我通过演示拱门和汽车模型进行分析，通过演示，让学生明白汽车过拱门单行道走中间。2、学生会根据立体图形画出几何图形，进行合理探究。）

利用三种方法进行探究，方法一、先引导学生通过已知汽车宽度、半径、求出能通过的汽车的最大高度，与已知高度进行比较进行决策；方法二、利用已知高、宽求能通过的最小拱门的半径，再与已知半径进行比较进行决策（这是课本的方法）；方法三、利用已知高、半径求能通过的汽车的最大宽度，与已知宽度进行比较进行决策（学生自己总结此方法）。本环节主要探究第一种，其他两种孩子自然就很容易想到。

三、巩固练习，反馈矫正---------我就是最棒的！

当堂小测验（为选作题）

1.一根旗杆在离地面6米处折裂,旗杆顶部落在离旗杆底部8米处.旗杆原来有（）米?(A类）

2.一根16米高的旗杆在某处折裂,旗杆顶部落在离旗杆底部8米处.求断裂处距离地面的高度?(B类）

3.老师想用一条36cm长的绳子围成一个直角三角形，期中一条边长度为12cm,求另外两边的长度？

四、感悟与反思（学生来结本节课的内容即学有所得）

通过这节课的学习活动你有哪些收获？

师生相互交流总结：

1．解决实际问题的方法是建立数学模型求解．

五、 布置异步作业

1、（A）基础达标：

（1）在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的直线距离相等,试问这棵树有多高?

（2）一大楼发生火灾，消防车立即赶到距大楼9米处，升起云梯到失火的窗口，已知云梯长15米，云梯底部距地面2.2米，则发生火灾的窗口距地面有多少米?

2、（B）拓展延伸：自编一道与勾股定理有关的应用题向与你水平相当的同学发出挑战。

六、教学设计反思

本节从生动有趣的问题情景出发，通过学生自主探究，运用勾股定理及其逆定理解决简单的实际问题，既巩固了基本知识点，又在将实际问题抽象成几何图形过程中，学会

观察，提高分析能力，渗透数学建摸思想．在设计中，我注重以下两点：

1．要创造性的利用好教材提供的素材

教材是“汽车过隧道”，我将它改为“汽车如何过拱门”，是一个生动有趣的问题，让学生充满了探究的欲望，对发展学生的空间观念很有好处．

2．合理使用教材提供的练习

本节课通过“第二站”和“第三站”把教材中的练习与例题重组，使练习有梯度，既巩固了基本知识点，又训练了学生的应用能力．

3．突破重点、突破难点的策略

在教学过程中教师应通过情景创设，激发兴趣，鼓励引导学生经历探索过程，得出结论，从而发展学生的数学应用能力，提高学生解决实际问题的能力．

4．分层教学

根据本班学生实际情况可在教学过程中选择：当堂测试和异步作业都分出A、B组，差异教学渗透每一个环节！

5．评价方式

根据新课标的评价理念，在教学过程中应关注学生的参与程度，关注活动中所反映出的思维水平，关注对实际问题的理解水平，关注学生对基本知识的掌握情况和应用勾股定理及逆定理解决实际问题的意识和能力．在教学过程中尊重学生的个体差异，对于学生的回答教师应给予恰当的评价与鼓励，并帮助学生树立学习数学的自信，充分发挥教育的价值．因此我设立了男孩女孩pk台,事实鼓励评价。

板书设计

教学反思

扫面二维码下载答案及文档