一、探索性因子分析简介
探索性因子分析往往会被使用于处理那些没有办法直接测量的变量上,比如一个人的抑郁水平。显然,你没有办法去直接去问别人:
“请给你的抑郁程度打个分(1到10,从低到高)?”
且不说这样会冒犯别人,而且很多人对所谓的抑郁程度丝毫没有概念,如果一个人能很好或者说很客观地评价自己的抑郁水平,那还要心理医生干什么呢?
相反地,我们需要这样地设问:
“请你给你最近的睡眠状况打分”或者“你最近是不是经常感到沮丧”等等,我们往往需要通过一些可以直接测量或者说相对客观的变量来推断一个人的抑郁水平。这些能被相对客观测量的变量被称为“验证变量”(Manifest Variable),而我们想要知道的抑郁水平则被称为潜在因子(latent factor)。
在正式开始EFA之前,我们再看看之前在主成分分析中得到的这张知觉图。
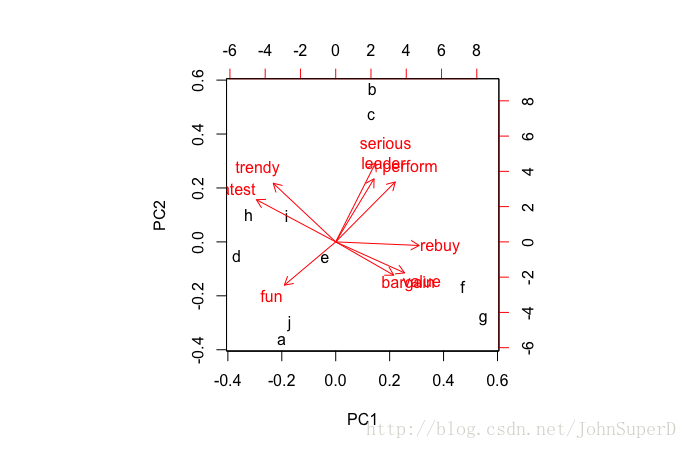
图中这些红色箭头是各个变量在主成分1和主成分2上的投影,你可以看到,有一些变量会比较靠近(因为是投影,图上只能是大概地反应真实状况),比如trendy变量(潮流度)和latest变量(最时髦度),确实这两个变量反映的其实是一回事。另外,serious、leader、perfrom似乎也有很强的相关性,这样我们是不是能够用一个新的变量来表示这原有的变量呢?另外,新生成的变量和原有变量的关系又是怎样的呢?这些问题正是EFA所要解答的。
二、R在因子分析中的应用
带着上面的问题,下面我们将:
data_EFA<-data_PCA
#注意:这是上一篇PCA的数据
str(data_EFA)#查看数据结构
sum(eigen(cor(data_EFA))$value>1)
#答案是3个因子
#应用factanal()
#外面的括号能够使运行结果显示出来
(EFA1<-factanal(data_EFA,factors = 3))
names(EFA1)上面的输出结果是这样的
Call:
factanal(x = data_EFA, factors = 3)
Uniquenesses:
perform leader latest fun serious bargain value trendy
0.624 0.327 0.005 0.794 0.530 0.302 0.202 0.524
rebuy
0.575
Loadings:
Factor1 Factor2 Factor3
perform 0.607
leader 0.810 0.106
latest -0.163 0.981
fun -0.398 0.205
serious 0.682
bargain 0.826 -0.122
value 0.867 -0.198
trendy -0.356 0.586
rebuy 0.499 0.296 -0.298
Factor1 Factor2 Factor3
SS loadings 1.853 1.752 1.510
Proportion Var 0.206 0.195 0.168
Cumulative Var 0.206 0.401 0.568
Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 64.57 on 12 degrees of freedom.
The p-value is 3.28e-09 关于EFA1的输出结果,最为重要的是要看loadings,代表了这些因子和原来变量的关系。
就拿因子1来说,你可以看到bargin、value、rebuy的数值是正的,而latest和trendy的数值是负的。说明因子1的方向bargin、value、rebuy一致,而与latest和trendy的方向相反。同时这很好地对应了前面的知觉图所展现的情况,即这两组变量所处的位置是相反的。
有一点需要说明的是,factanal()的初始设定是不允许因子之间存在相关性的。如果你允许潜在因子之间存在相关性的话,试试把rotation参数设置为“oblimin”(需要现加载GPArotation)。
library(GPArotation)
(EFA2<-factanal(data_EFA,factors = 3,
rotation = "oblimin"))EFA2的输出结果如下
Call:
factanal(x = data_EFA, factors = 3,
rotation = "oblimin")
Uniquenesses:
perform leader latest fun serious bargain
0.624 0.327 0.005 0.794 0.530 0.302
value trendy rebuy
0.202 0.524 0.575
Loadings:
Factor1 Factor2 Factor3
perform 0.601
leader 0.816
latest 1.009
fun -0.381 0.229
serious 0.689
bargain 0.859
value 0.880
trendy -0.267 0.128 0.538
rebuy 0.448 0.255 -0.226
Factor1 Factor2 Factor3
SS loadings 1.789 1.733 1.430
Proportion Var 0.199 0.193 0.159
Cumulative Var 0.199 0.391 0.550
Factor Correlations:
Factor1 Factor2 Factor3
Factor1 1.0000 -0.388 0.0368
Factor2 -0.3884 1.000 -0.1091
Factor3 0.0368 -0.109 1.0000
Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 64.57 on 12 degrees of freedom.
The p-value is 3.28e-09 首先可以看到EFA2的loadings与EFA1的略有不同,但变化不是很大,而且看到EFA2的三因子的累计方差(Cumulative Var)只是略少于EFA1,所以EFA2可以是一个好的选择。还有一点,EFA2比EFA1多了一个Factor Correlations的矩阵。你可以看到因子1和因子2存在着-0.39的相关性。考虑到因子1和因子2的构成变量,这确实一个很不错的发现,也就是说当我们想改善产品在因子1(代表着value、bargain,rebuy)的表现的时候,可能需要付出的代价是牺牲因子2(代表着perform、leader,serious), 而这就要看公司的对产品市场定位和预期的收益了。
三、查看因子得分
如果我想知道各个产品在各个因子上的得分怎么办?我可以在factanal()里加上scores在这一参数。
EFA3<-factanal(data_EFA,factors = 3,
rotation = "oblimin",scores = "Bartlett")
EFA_score<-data.frame(EFA3$scores)
EFA_score$brand<-brand.rating$brand
head(EFA_score)我们可以用dplyr包的group_by()和summarise_all()来计算各个品牌在各个因子上的平均得分。
library(dplyr)
library(tidyr)
EFA_scroe_mean<-EFA_score%>%
group_by(brand)%>%
summarise_all(mean)
head(EFA_scroe_mean)EFA_score_mean :
# A tibble: 10 x 4
brand Factor1 Factor2 Factor3
老实说没人会喜欢这样密密麻麻的数据的,所以为了更好地呈现结果,我们可以结合数据可视化的方法。
四、对得分进行可视化
在可视化之前,我们要用gather()处理一下数据。
library(tidyr)
EFA_score_heat<-EFA_scroe_mean%>%
gather(FACTOR,Value,-brand)EFA_score_heat的头10行:
# A tibble: 10 x 3
brand FACTOR Value
用ggplot2的把上面的数据做成热图
p2<-ggplot(EFA_score_heat,
aes(FACTOR,brand))+
geom_tile(aes(fill=Value))+
geom_text(aes(label=round(Value,2)),
size=4.5)
p2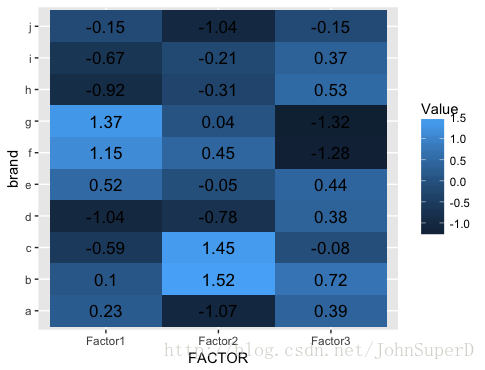
如果想把图片做的更简洁清晰地话,需要多一些代码:
p2<-p2+scale_fill_gradient2(low = "blue",
high="red",mid = "white",midpoint = 0)+
title="Mean factor score by brand",
fill="Score")+
scale_x_discrete(expand = c(0,0))+
scale_y_discrete(expand = c(0,0))+
theme(plot.title = element_text(hjust = 0.5,
face = "bold",size=12))
p2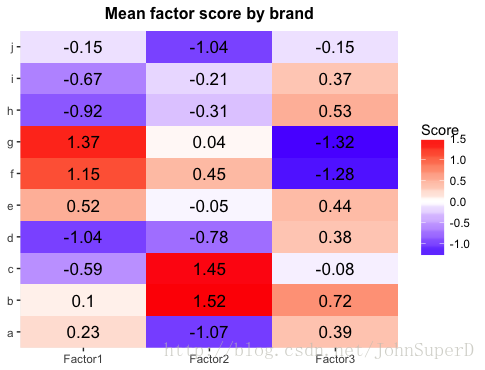
可以看到产品g的因子1的得分很高,因子3的得分则最低。同时我们也可以得到其他产品的因子得分。那么,我们要知道这些数据又有什么价值呢?当你有了各种产品的销量的时候就有用了,你可以把这些因子得分作为预测变量,把销量作为响应变量,来查看各个因子对结果的影响(注意,进行回归分析的时候不要使用EFA_score_mean数据,而要使用EFA_score数据,也就是使用按产品平均化以前的数据)。当然,一般来说要进行回归分析的话,最好还是使用原来的变量,因为经过因子分析处理过后,会损失不少信息。但是,如果原来的变量非常多,前几个因子又很好地还原了原来数据的信息,那么用因子来作为预测变量进行回归分析也不失为一种好选择,因为那样会大大减少线性模型的复杂程度(想想看,如果原始数据有几十个变量,光展示一个完整的线性模型估计都得用掉一张纸)。
五、小结
1、EFA是一种通过可以客观、直接验证的变量来寻找潜在因子的分析方法。在R中,我们可以使用factanal()来完成。
2、如果你允许因子之间有相关性的话,可以修改factanal()的rotation参数。
3,在EFA的输出结果中,loadings最为重要,通过loadings可以知道潜在因子与原变量之间的关系。
4,有时候可以把因子得分作为预测变量,以简化线性模型的复杂程度。



发表评论