验证性因子分析作为结构方程的前提条件, 你在做结构方程(以后称SEM)之前, 必须先做验证性因子分析(CFA), 但是很多人并不理解, 认为如果SEM结果好, 那么CFA结果必然也好, 如果SEM结果差, CFA结果好也没用, 所以CFA作为SEM的必要非充分条件, 其实不需要单独去做。

实际上, CFA存在的目的不仅仅是为了让SEM结果好, 还有一个目的就是证明研究效度, 一个变量具有效度的意思是变量能够代表它背后的意义, 比如你研究的是幸福感, 你也有一个变量代表幸福感, 收集了幸福感的数据, 但是这个数据真的是幸福感吗? 变量分数高真的代表这个人的幸福感高吗? 如果你无法证明这一点, 你的研究就没有效度。

我们看一个典型的例子来说明以上结论。

这是一篇发表过的文章, 它包含的变量有这些:

变量说明

它的模型是这样的:

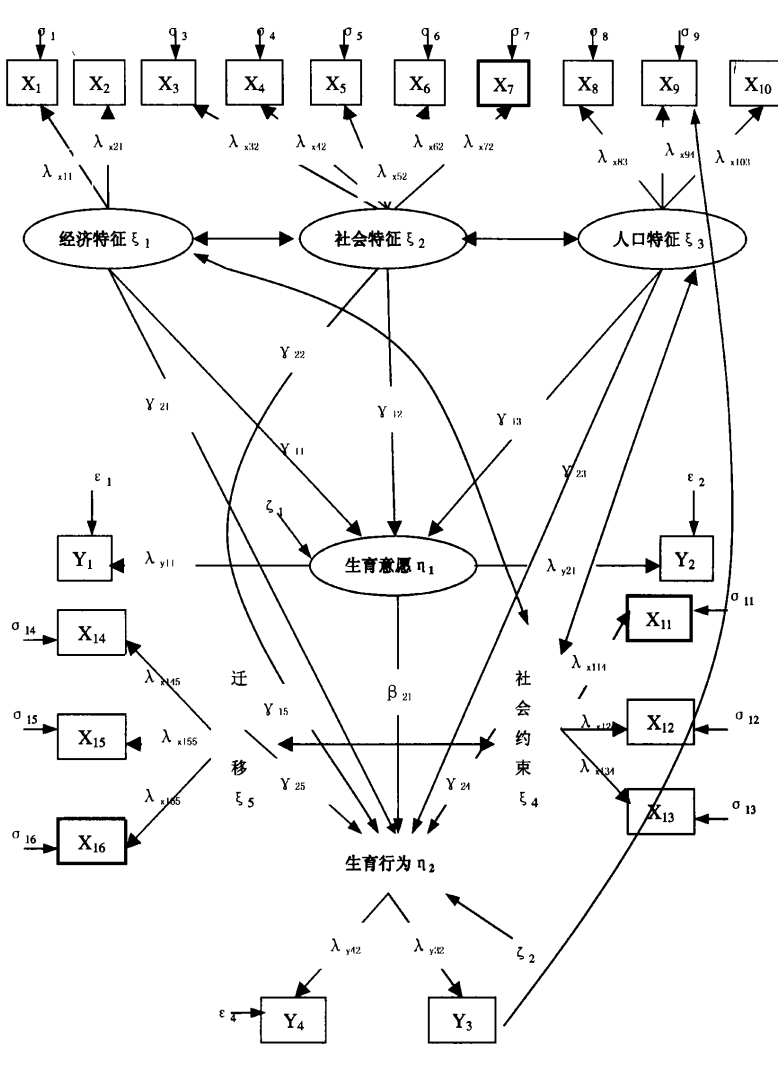
模型

最后的结果似乎很好(所有拟合指标达标):

模型拟合

然后因子载荷不是很理想, 大量不显著的

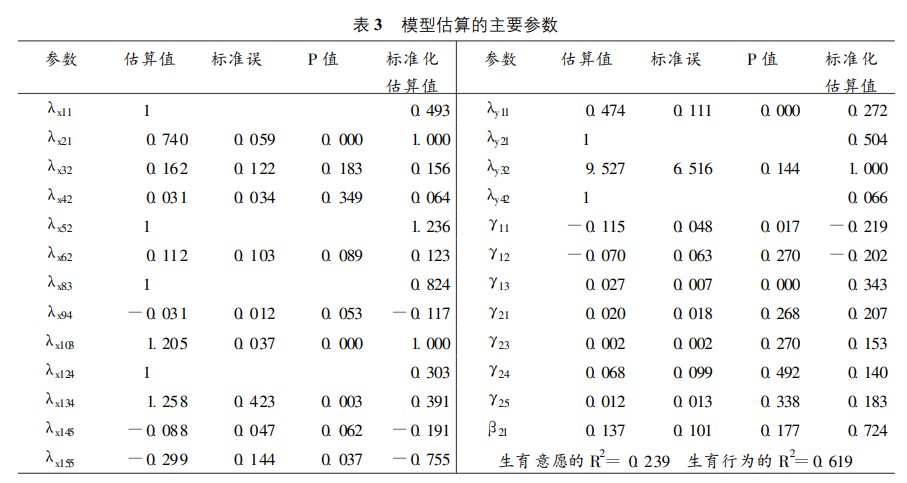
路径系数的检验

竟然还做了中介效应, 显然它没有做Bootstrap显著性检验, 这样无法证明结论:

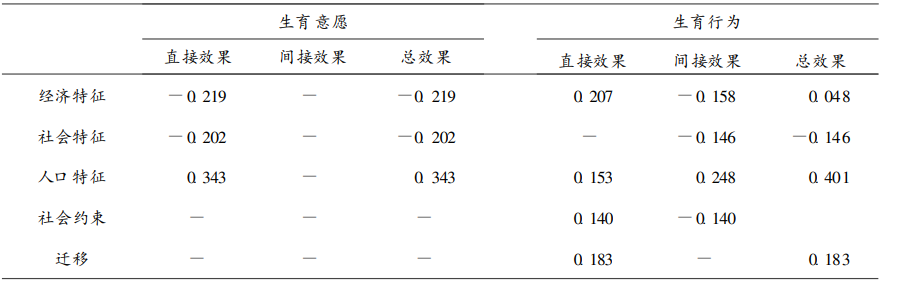
中介效应

作者可能自认为自己做了一个相当不错的研究, 下面列出作者的部分结论, 然后我们后面再讨论:

对生育行为最大的影响因素是生育意愿

从各影响因素看, 不管是对生育意愿还是生育行为 ,人口特征的影响作用都是最大的

经济特征对生育意愿和生育行为的影响同样也不容忽视。然而, 它们的作用方向却是相反的 。个人经济水平的提高明显对生育意愿产生负作用, 但为什么它同时又会引起生育行为的水平提高这样一个矛盾的结论呢

针对这些结论, 我们可以找茬的地方有很多, 但是需要在视频里慢慢讲, 我们先列出几点提示:

潜变量的效度没有检验

不显著的路径系数只能当作0来下结论

比较两个路径系数大小, 可以直接看他们表面的大小吗

由于作者没有做CFA, 导致他的任何结论都不具有效度, 比如他说"人口特征的影响作用都是最 大", 人口特征这个"潜变量"实际上不存在, 它的测量指标有三个(X8 X9 X10), 其中只有1个指标的因子载荷是显著, 这意味着, 潜变量完全不能代表这三个指标, 也就是说虽然潜变量对别的变量有影响, 但是潜变量是谁? 你没有说清楚, 或者无法证明。