课程题库分享到空间分享到新浪微博分享到QQ分享到微信

2022年成考高起点《数学(文史)》每日一练试题11月20日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

答 案：C

2、,

答 案：C

3、设双曲线

的渐近线的斜率为

答 案：D

解 析：根据双曲线渐近线的斜率公式

,所以题中则为

，答案为：D

4、

答 案：B

解 析：本题主要考查的知识点为简易逻辑．

【应试指导】 故甲是乙的充分不必要条件．

主观题

1、(I)求E的离心率;

答 案：由题设知△AF1F2为直角三角形，且

设焦距|F1F2|= 2c，则|AF2|=3/2c如，|AF1|=5/2c，2a=|AF1|+|AF2|= 4c.所以离心率

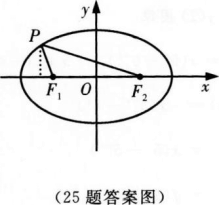
2、椭圆的焦点F1(-1，0)，F2(1，0)，｜F1F2｜是｜PF1｜和｜PF2｜的等差中项。

(Ⅰ)求椭圆方程；

(Ⅱ)若∠F2F1P=120°，求△PF1F2的面积。

答 案：

(Ⅱ)如图，设P点的横坐标为-1-m(m>0)，

3、求函数

的最大值与最小值，以及使函数取得这些值的x的集合。

答 案：

4、已知函数f(x)=x3-4x2。 (I)确定函数f(x)在哪个区问是增函数，在哪个区间是减函数； (II)求函数f(x)在区间[0,4]上的最大值和最小值．

答 案：

填空题

1、已知sinα-cosα=a，计算sinαcosα=（）。

答 案：

解 析：∵sinα-cosα=a，∴(sinα-cosα)2=a2，

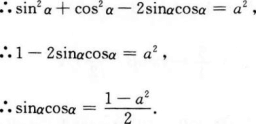
2、将一颗骰子掷2次，则2次得到的点数之和为3的概率是（）

答 案：0

解 析：【考情点拨】本题主要考查的知识点为偶函数的性质．【应试指导】