毛细管效应的研究历史

当把一个玻璃毛细管插入水中，很明显能够看到毛细管中的水会上升，最终停留在一个比水平面高的位置，这就是毛细管上升效应。这么一个看似简单的过程，却是界面浸润性领域的研究基石，人类从初步意识到这个现象到完全理解其规律经历了三百多年的历史。

图1 毛细管上升现象

达芬奇（Leonardo da Vinci 1452–1519）是第一个有记录地观察这个现象，他相当大胆地在笔记中做出设想，认为山上泉水就是源于这一系列组成网络的毛细管提供的升力作用而形成的。Jacques Rohault (1620–1675)，做出的解释是，毛细管上升的是由于空气不稳定，空气可以在窄的毛细管中进行流通，创造出真空来使液体上升的。天文学家Geminiano Montanari (1633–1687) 把毛细上升现象和植物流出的汁液做了对比研究。以观察木星的卫星和动物行为著名的Giovanni Borelli (1608–1679)，在1670年提出了毛细上升高度和毛细管半径成反比的关系。

Francis Hauksbee (1713)是第一个系统地研究毛细管上升现象，然而作为故事的重要主角，他却被不公平地遗忘了。他使用染色的液体和玻璃管做了一系列实验，并从中得出了如下结论：

毛细管上升现象，在空气中和真空中都会发生。（反驳了上面的空气传递的观点）毛细管上升效应不只是存在于圆柱形状的毛细管里。他也存在于两块平行的固体板中，但是当板子距离与毛细管直径相等时，板子中间液体上升的高度是毛细管内部液体上升高度的一半。毛细管上升效应也存在与其他固体（大理石，黄铜）和其他液体（乙醇，油等）的相互作用中。毛细管中液体上升的高度与毛细管的壁厚无关。他使用不同外壁厚度（内径相同）的玻璃管，发现上升的高度几乎相同。

牛顿是Francis Hauksbee的同事，他在自己的光学专著中描述了这些实验结果，不幸地是，却并没有提及Hauksbee的名字。在1712年，被称为泰勒展开式之父的泰勒，做了一个两个平板间毛细管效应的实验。他惊奇地发现，固体壁边缘的液面轮廓竟然看着像一条双曲线。之后Francis Hauksbee通过自己精确的测量数据证实了这个结论。然而，基于种种原因，这些人最终都没能把自己的名字写在毛细管上升效应的定律里。

幸运之神反而降落到一个叫James Jurin(1684–1750)的英国心理学家身上，他在1718年独立地证明了毛细管中液体上升的高度和毛细管的直径成反比关系，因此毛细管效应也被称为“Jurin‘s law”。 又过了约一个世纪，在1806年，这个现象背后的原因才最终被Laplace的理论完全揭示。

毛细管效应的规律:能量的角度

Laplace的理论指出，固气界面和固液界面都存在着表面能分别记为γso和γsl, 只有γso大于γsl的时候，毛细管中的液体才会上升。我们可以定义一个上升参数I为：

公式1 毛细管上升参数I的定义

当I大于零时，这时，毛细管上升就会减少固气界面（被表面能小的固液界面替代），因而会降低体系的能量，这时毛细管中液体会上升。当I小于零时，毛细管下降会减少固液界面（被表面能小的固气界面替代），因而也会降低体系能量，所以毛细管会下降。其实使用杨氏方程（γso – γsl = γcosθE）把上式代换，可以得到I = γcosθE ，这样就能把问题转为接触角θE大于或小于90°的问题，不再赘述。

下面分析毛细管效应中的能量问题。既然毛细管上升会降低能量，那么能量最低时的液面高度就是最后液面稳定的高度。

设液面上升的液体柱高度为h，玻璃管半径为R，那么对于这个液体柱的能量E 包括表面能和重力势能，关系为：

公式2 毛细管上升液体柱能量公式

式中右边第一项就是表面能，第二项就是重力势能。这个关系式是在上升高度h远远大于半径R时才成立，这时才可以把弯液面的形貌给简化为平面来计算表面能和重力势能。

把上面关系 I = γcosθE带入并通过微分，求能量E最低时的H值，可得其关系为：

公式3 毛细管上升公式

这就是毛细管上升的高度公式，通过能量分析，更能明确地感到这个过程是个自发过程。而不是有人认为的，上升液体的重力势能没有来源，从而违反热力学第二定律。

需要指出的是，这个公式只有在毛细管半径R远小于H的情形下才会精确，一般要求R远小于毛细作用长度（2.71mm）。如果不满足这个情形，公式3必须做相应的修正，在19世纪，这个公式被Laplace，Poisson, Gauss 和Rayleigh 分别修正过。

公式3与很多前人的实验现象相吻合。比如，它符合上升高度和毛细管半径成反比的关系。其次，当接触角θE大于90°时，H为负值，它同样适用于毛细下降的情形。还有一个情形，就是如果毛细管的高度h小于这个能量最低时的高度H时，会发生什么现象，液体会不会喷涌而出，从而可以利用这种爆发的能量。答案当然是不会的，当h很小时，液体会充满整个毛细管，这时毛细管内的液面不再是稳定接触角θE，而会大于这个值，从而使H变小，直到平衡，这个要从力的观点去解释更为方便。

毛细管上升的规律公式:力的观点

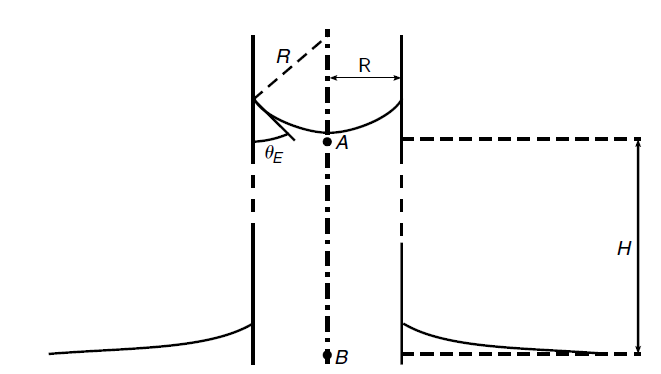
图2 毛细管上升的压强关系

国内的教材中，几乎都是力的角度来推出毛细管上升的公式的。而且，都是默认毛细作用力与重力的平衡，这种默认让不理解表面张力的同学难以接受。下面从外文教材中给出一个比较新的思路，去推出毛细作用力的大小，而不是直接默认。

对于毛细管上升的液面，其液面分析如图2所示，由Laplace附加压力方程可以知道，在紧挨着液体界面处，点A的压强为：

公式4 A点的压强公式

公式4中，P0为大气压强，PA为A点的压强。然后再看与水平位置相同高度的B点，以B点为参考点，则A点的压强为B点的静压强减去pgh，B点的压强和大气压压强是相同的，从而得出：

公式5 A点压强建立的等式关系

化简一下公式5就推出了公式3的方程。国内的很多教材，直接从毛细作用力提供液体重力，直接给出了公式5的简化版，这样跳跃性有点太大。

下面我们推出毛细作用稳定时体系中毛细作用力的大小和方向是什么。

在液体上升稳定后，由于毛细管内部的液体高于水平面的高度。所以一定存在一个力F，这个力的作用可以平衡这部分液体的重力，从而使液面稳定。根据力的平衡，其大小为：

公式6 存在的力F使液面高于平衡液面

把公式2中H带入F即可得出F的关系式为：

公式7 存在的力F的计算公式

通过观察公式7可知，这个力等于液体表面张力与液面上固液气三相接触线周长的乘积。由于这个力是在毛细上升过程稳定液面稳定的力，可以称为毛细作用力。此毛细作用力作用在三相接触线上，方向平行于固气界面，竖直向上。下面我们可以计算出在三相接触线上，单位长度所有的毛细作用力为：

公式8 单位长度下的毛细作用力

这样又回到了最上面公式一的上升参数I的物理含义。I即是当液面稳定后，单位长度下三相接触线所受到的毛细作用力。

从上面可知，这个力f与重力相互抵消，从而使液面稳定。下面我们分析，当毛细管较短时，重力较小，f较大，这时毛细管中的液体能否喷涌而出。

从公式8可以看出，这个力f和接触角θE有关系。我们知道，当液面稳态时其接触角为θE。 然而在外力作用下，这个接触角可以增大。接触角增大伴随着f的减小。甚至在毛细管顶端，液面由凹液面变为凸液面，此时f为负值，根本无法提供任何有效的升力。所以结果是，水会充满毛细管，在毛细管的顶端位置，液面会变为θE到π的中间的值θ，这个值可以调控f的大小，来正好平衡上升液体的重力，如图3所示。这个中间值θ可以通过公式3轻易地算出来。

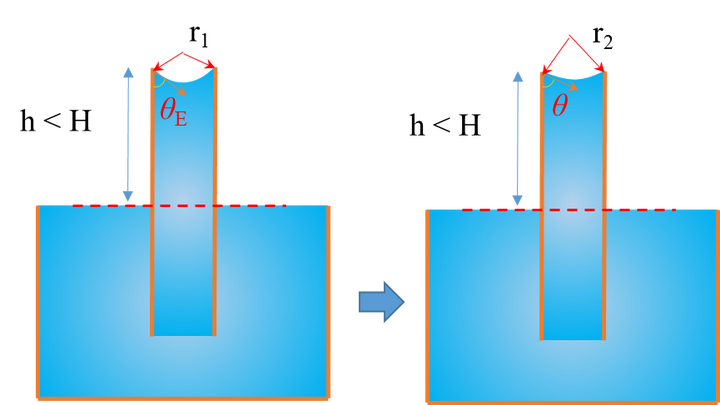
图3 毛细管力大于重力时，毛细管上升的界面变化过程

注：此文章受以下问题激发而整理：

参考文献：De Gennes, P. G., Brochard-Wyart, F., & Quéré, D. (2013).Capillarity and wetting phenomena: drops, bubbles, pearls, waves. Springer Science & Business Media.