学习数学唯一正确的方式，就是重新发明数学。

-荷兰数学家、教育家弗莱登塔尔

1 多边形计算世界纪录

德国数学家鲁道夫将一生献给了圆周率计算。1596年，鲁道夫通过60 × 2^33（515396075520）个多边形算出20位Π；1610年，他再次改写记录，将多边形的数量增加到2^62（4611686018427387904）个，将人类多边形计算圆周率法推向极致。

将鲁道夫计算圆周率排名第1位，是想表达小麦老师对那一代数学家的敬意，ta们仰望星空，追求卓越，是我们永远的标杆和榜样。

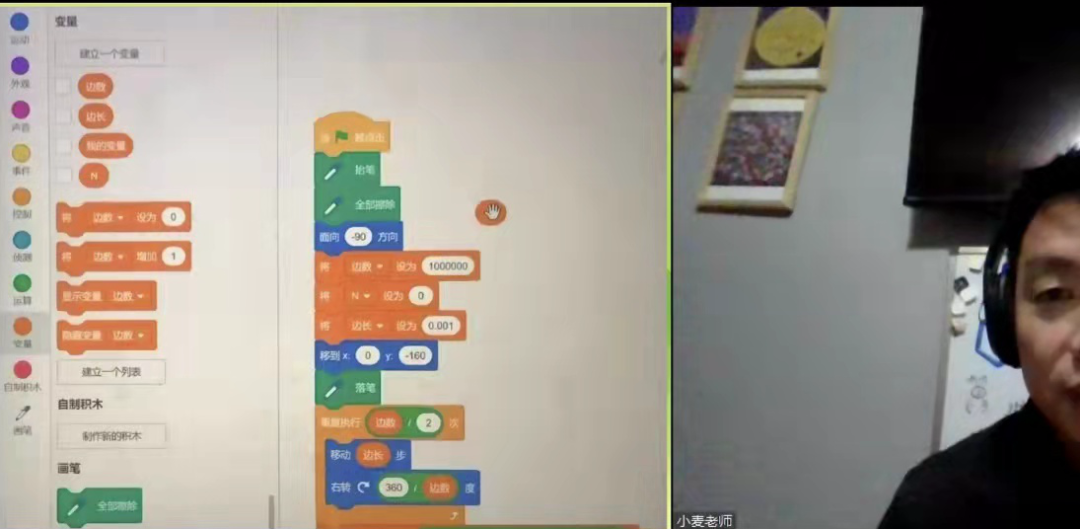
通过Scratch编程完成100万多边形计算

2 最美欧拉公式

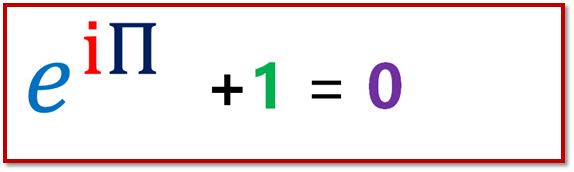
e：自然常数，i：虚数，Π：圆周率

1748年，瑞士数学家数学之王欧拉发现最美的欧拉恒等式，该公式将数学中最基本的五个数字整合在了一起，被几乎所有的人认为是数学中最美的公式，被比作是莎士比亚的十四行诗。

备注：在所有的最美公式排行榜中，欧拉公式必定第一，第二值得我们敬畏。

3 莱布尼茨公式

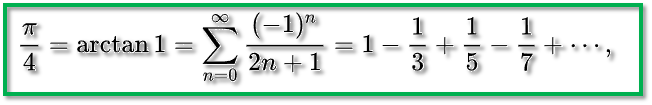
1673年，德国数学家莱布尼茨发现奇数与圆周率之间的关系并证明，开启了人们采用无穷级数计算圆周率的新纪元。

孩子们可以通过编程来体验无穷级数计算圆周率的过程，莱布尼茨计算公式收敛速度非常慢，需要628项才能得到3.14。

Matlab编程代码

4 牛顿圆周率计算公式

1676年，英国科学家、数学家牛顿发现上述公式，该公式改进了收敛速度，只需要3项就能得到3.14，如果n=9，则可精确到小数点后8位。

5 梅钦公式

1706年，英国天文学家、数学家梅钦（John Machin）通过他发明的梅钦公式将圆周率精确到第100位。梅钦公式收敛较快，每计算一项可得到π的1.4位十进制精度。

6、欧拉巴塞尔公式

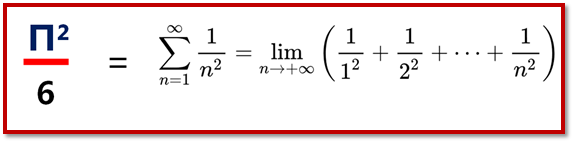
1644年，皮耶特罗·门戈利（peter mingoli）提出自然数平方倒数问题，该问最终由莱昂哈德·欧拉在1735年解决，并以欧拉的出生地巴塞尔命名，被人们称为巴塞尔问题。

7 最丑但最有效的拉马努金公式

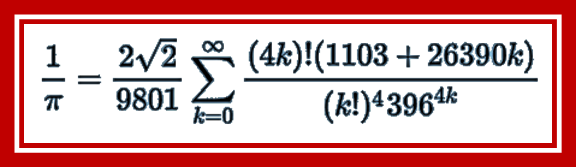
1914年，印度数学家拉马努金一口气发现14个圆周率计算公式。虽然被后世评为最丑公式之一，但却是最有效的圆周率计算公式。当 n=1时，竟然可以算出7位有效圆周率；当 n=2时，可算出16位有效圆周率。神一样的天才当之无愧。

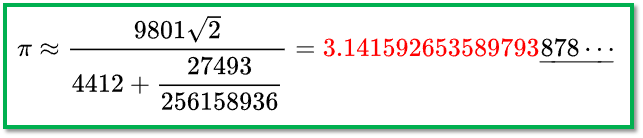
8欧式几何圆面积公式

公元前3 世纪，古希腊数学家阿基米德《圆的度量》，圆面积等于一条直角边长等于圆半径，另一条直角边长为圆周长的直角三角形面积。

公元263年，中国数学家刘徽采用割圆术方法计算圆面积。

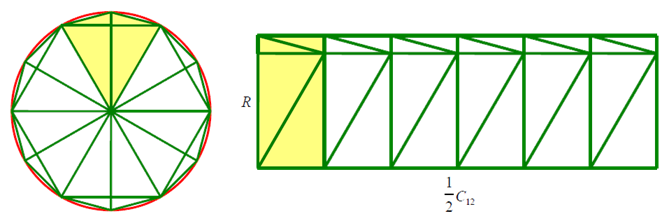
刘徽：割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣。

15世纪，意大利著名的艺术家、发明家达芬奇发明圆面积计算方法。

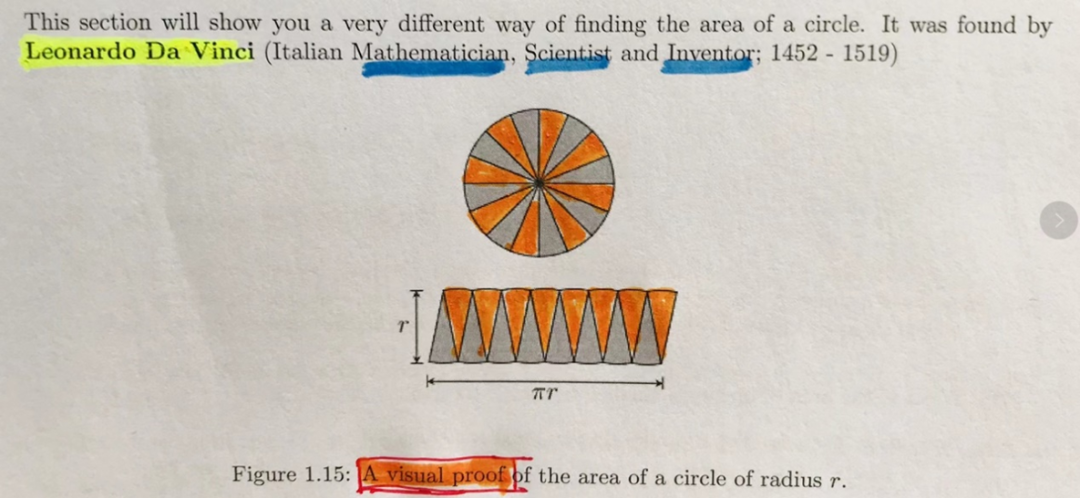
17世纪，德国著名天文学家和数学家开普勒在自己的婚礼上发明圆面积计算的创新方法。

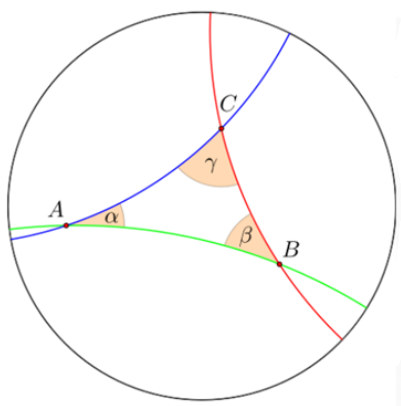
9 非欧几何面积公式

该公式分别由俄国数学家巴罗切夫斯基（1829年）与匈牙利数学家鲍耶（1832年）发现。

10 霍金黑洞温度公式

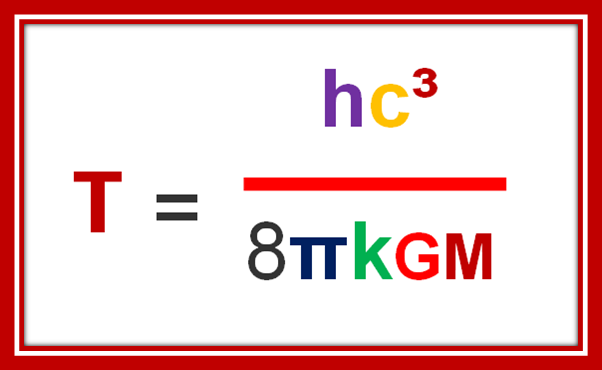
h：普朗克常数、c：光速、 π：圆周率、K：玻尔兹曼常数、G：万有引力常数、M：黑洞的质量

1974年，世界最伟大的物理学家霍金在运用量子力学研究黑洞邻近弯曲时空中的粒子时，发现黑洞温度，并提出上述计算公式，将量子理论、广义相对论和热力学全部联系在了一起。

2018年3月14日，霍金逝世，享年76岁，他让3月14日变得更加伟大。

文案©小麦老师

视频号

抖音号