人对于数的认识，是与身俱来的本能。人类通过自然演化，具有先天的数学认知能力。大量的经验研究表明，刚出生的婴儿具有简单的数量识别以及简单的算术能力。但是这种简单的算术能力是无法天然的发展为更复杂的数学系统。一个文明要向更复杂的数学系统迈进，需要更强大的物质基础，也需要更精细的社会协作。

数学的发展仰赖于人类社群中精英分子。数学历史的研究，往往是一种英雄史的研究。另一方面，地理环境等等长时段的历史结构，往往是被人忽视的。因为他们在一代人或者几代人的生存过程中都可能是看不到的，它很缓慢的发展着，甚至可以理解为接近静止的时间运动。然而英雄历史本身不可能独立于长时段历史所存在，他必定是内嵌于长时段的历史结构之中的。如果人们想要以新的眼观察数学历史，就必须与历史的这种长期缓慢发展联系起来。 人与历史的关系上， 与其说是人创造历史，不如说是历史创造人。

很多人认为古希腊的数学中心位于巴尔干半岛上的雅典，柯林斯等希腊本土城邦。事实上古希腊数学的中心并不在希腊本土，而在于地中海对岸的埃及城市亚历山大港。我们之所以称他们是古希腊数学，是因为这个时期的埃及是亚历山大大帝征服之后的希腊化的埃及。我们现在所熟知的希腊数学家，欧几里得、阿基米德、埃拉托塞尼、海伦，丢番图，希帕提娅，几乎都在这个北非港口城市为中心展开他们的学习和研究活动。

为什么古希腊数学会集中于这个城市，而不是希腊哲学的中心雅典？最重要的原因在于，数学的研究和学习非常仰赖莎草纸这一媒介。莎草纸虽然便于书写和作图，但是它也有很明显的缺点，它会因时间、环境因素变旧，发生突变性化学反应，导致莎草纸卷损毁。在地中海北岸相对于北非更加阴冷潮湿，人们为了保存文献不得不反复抄写。例如，罗马皇帝泰西德斯为了妥善保管好记载先人事迹的历史著作，曾命令官方抄写员每年抄写10个副本，然后送到图书馆收藏。

亚历山大属热带沙漠气候，但又相对埃及内陆更为湿润，全年平均气温在18-30度年均降水200毫米。托勒密王朝时期，莎草纸的产量增加，质量改善。纸莎草由人工栽培，一年四季可以收割，王室垄断，调控销售，但是私人也可以种植加工。最好的纸由国家以固定价格收购，质量差的可以在民间销售。亚历山大里港成为一个纸张买卖盛行的城市。一份公元前258年--前257年的文献材料显示，财务大臣在33天里共收下434卷纸莎草纸文件。气候宜人居住又相对干燥的环境，为莎草纸类的文献保存和交流提供了良好的环境条件。

正是由于这样一个优渥的气候和物质环境，让亚历山大的数学家可以大量使用便宜的莎草纸。这些数学家可以在纸张上尽可能的表述推理逻辑，进行细致而精确的几何作图。阿基米德用纸草卷写了很多作品，大部份以私人信件的方式送给亚历山卓图书馆馆长埃拉托斯尼斯，而后者就把这些作品存放在亚历山大图书馆中。承载着来自于各地的数学知识的莎草纸汇聚于亚历山大，同时这座城市也像一块磁石一样吸引着整个地中海世界的数学家们来此学习、传授、交流数学知识。经过数代数学家们的积累，在亚历山大便形成了人类历史上第一个数学家共同体——亚历山大学派。

同一纬度线，同一时代的古代中国，则没有如此丰厚的物质条件。中国从战国到魏晋，近500年的漫长历史中，中国文化都是围绕着简牍为中心的。

清华简--筮法--局部

我们看一下，清华简中这张难得一见的竹简图案，就不难明白简牍传承知识的困难所在。我们不可能要求在这种物质条件下，中国先民去考察，平行、垂直、全等、相似，这些需要精细图形才能产生的概念。

另一方面简牍的编写困难，还造成了中国叙事传统的缩略性。司马迁耗时十数年，用了近五十二万余字记述了中国从传说中的黄帝到汉武帝太初四年长达3000年左右的历史，而一本译为中文就有60余万字。我们不可能要求在这种物质条件下，中国古代数学家去用整整48个命题作为勾股定理的预备定理。

由于简牍在传播上的高成本，简牍的抄写和传播绝大多数都是由政府机构集中力量不计成本组织完成。与图书馆、学院为学术中心的希腊文明不同，中国的政府部门成为了中国最早的学术中心，汉代刘向 刘歆父子领导了中国历史上第一次大规模的图书整理。

汉兴，改秦之败，大收篇籍，广开献书之路。迄孝武世，书缺简脱，礼坏乐崩，圣上喟然而称曰：“朕甚闵焉！”于是建藏书之策，置写书之官，下及诸子传说，皆充秘府。至成帝时，以书颇散亡，使谒者陈农求遗书于天下。诏光禄大夫刘向校经传诸子诗赋，步兵校尉任宏校兵书，太史令尹咸校数术，侍医李柱国校方技。每一书已，向辄条其篇目，撮其指意，录而奏之。会向卒，哀帝复使向子侍中奉车都尉歆卒父业。歆于是总群书而奏其七略，故有辑略，有六艺略，有诸子略，有诗赋略，有兵书略，有术数略，有方技略。——

至此之后整理图书和修史一样成为历朝历代中国特有的历史传统，北宋的,明代的,清代的，我们现在所能看到的绝大部分典籍都是依靠这种官方的知识和书籍整理才得以存续下来。

在这个知识整理的过程中国的官吏阶层成为了最早的学者群体，也无疑成为学术传播的中坚力量。1975年12月出土于中国湖北省云梦县城关睡虎地。墓穴里是一个秦朝名叫“喜”的基层官吏，喜有多热爱自己的工作呢？陪伴他下葬的不是常见的青铜器、金器、玉器，而是他工作时的秦简。考古人员打开墓穴时，他们发现的情形大概就是下图的样子。尽管位卑言轻，但他一定非常自豪满足于自己的工作。

1983年的张家山汉墓中的另一位秦末汉初的基层官吏，把一部自己研习的数学典籍带入了自己的墓葬。正如阿基米德给自己的墓碑上刻上”球內接圓柱“，丢番图在自己的墓碑上刻上算术谜题一样，这些中国古代官吏选择学术作品作为陪葬，无不说明了那个时代的官吏阶层对自己身上这份传承知识职责的重视和珍爱。

中国古代的数学正是在这样一个细致、严谨的处女座官僚体系中得以代代相传。在这些官吏身上数学与法律政令发生了奇妙的化学反应，他们让中国数学突破了简牍的困境，闯出了一条数算法化的道路。

莎草纸的便利带给了古希腊数学带来了精致的演绎风格。古希腊数学家从必要的公设出发，赋予几何学以逻辑结论的特征形式。但是古希腊数学家，显然没有意识到，虽然数学上的结论是从假设前提得出的必然推论，但是前提本身则完全是任意选取的，只要服从内在的相容性即可。希腊几何学并不像今天的数学那样，大体上是由假设命题所构成的形式逻辑，而是一副现实世界的理想化的图景。欧几里得的公理，公设和定义实际上都是由常识所总结的，他的几何学始终跟空间直观紧密的联系在一起。普罗克拉斯告诉我们，欧几里得曾经对他的前辈流于粗疏的命题，重新加以严格证明。是一本以“精致的直觉”为前提和基础，通过逻辑演绎进行知识再梳理的著作，它不允许“朴素的直观“有自由活动的余地。这就如一栋高楼大厦，建成之前需要各种脚手架和辅助设施，但是一旦完工这些脚手架显然就不应该再出现。

对于中国数学家而言，这个世界向他们关上了一扇窗，但也为他们打开了一道门。中国统一度量衡的历史进程为中国数学家打开了数据映射转换的大门。借助算筹“可编程”的特性，线性函数间映射转换被中国数学家运用的如火纯青。他们对数学的认知上，显然没有地球另一端的同行们来的更为精致化逻辑化，相反他们将中国算法数学建立在“朴素的直观”上。以现代人的眼光来看他们的很多结论无法和的庞大精致体系相比拟的。比如说，对于刘徽在开方不尽的问题上的定性，学界还是有诸多争论。台湾的李国伟教授认为

由于刘徽并没有推导出，无理数和有理数之间的逻辑矛盾，除了反映有些是平方数、有些不是平方数外，似乎还没有引导出对更深层次差异的认识——《九章算術》與不可公度量

这种说法对于接受过现代数学系统教育的人而言很容易接受的。我们现代人读要比读其他的古代数学书籍来的更为亲切熟悉。因为我们现代人从小学到大学传授的数学知识体系，实际上都是经过18世纪后的数学家们利用逻辑工具进行彻底改造整理的结果。我们学习的数学的整体风格大体是接近于这种逻辑再整理的文本。然而对于逻辑再整理之前的数学又是如何的呢？我们其实知之甚少，对于我们而言大厦是熟悉的，而脚手架是陌生的。

对于欧几里得之前的古代希腊数学，我们所知不多。对于他们是如何从零散的几何知识出发构建这栋几何大厦的过程我们也不甚了了。诞生赋予我们一种近似“神启“的横空出世之感。事实真是这样吗？

马克.吐温说:'历史不会重复，但会押韵"。

我们不妨考察一下一千多年之后，欧洲人对于创立微积分的历程，就会对这种“神启“有更现实的认知。现在我们公认，牛顿和莱布尼兹他们同时创立了微积分。然而微积分的真正达到现代意义的严格性定义和证明，是在牛顿之后200多年由柯西完成的。Carl.B.Boyer在他的中这样写到

从微积分的发展观点来看，欧几里得的表现出一种枯燥无味的讲究严格的顽固性，阻碍了那些新的思想和发现的生长。欧几里得的著作代表了一切数学思想的最综合形式——对一组前提的逻辑关系做演绎推理的结晶。不过，继他的几何学之后的几个世纪中，分析研究往往是建立在经验观察或者并不很审慎的直观基础上，并时常还是在先验的思辨的基础上进行的。微积分的概念主要是从这类探索中产生而不是欧几里得的严密思想中进一步发展起来的。

正如Boyer所说，牛顿时代的流术法的诞生，与其说它基于欧几里得的理性精神，不如说他更接近于刘徽式的经验直觉。

牛顿的流术法首先是以猜测，广义二项式定理为基础的。引领牛顿发现二项式定理的前导问题是为了计算圆周率 \pi 。考虑单位圆 x^2+y^2=1 所在的第一象限面积，算式如下

\displaystyle \frac{\pi}{4}=\int_0^1\sqrt{1-x^2}dx

牛顿的难题是如何以无穷级数表示 (1-x^2)^{1/2} ？他考察较为单纯的 (1+x)^r 展开式。当 r 是正整数时，前面几个式子为

\displaystyle\begin{aligned} (1+x)^0&=1+0\cdot x+0\cdot x^2+0\cdot x^3+0\cdot x^4+0\cdot x^5+\cdots\\ (1+x)^1&=1+1\cdot x+0\cdot x^2+0\cdot x^3+0\cdot x^4+0\cdot x^5+\cdots\\ (1+x)^2&=1+2\cdot x+1\cdot x^2+0\cdot x^3+0\cdot x^4+0\cdot x^5+\cdots\\ (1+x)^3&=1+3\cdot x+3\cdot x^2+1\cdot x^3+0\cdot x^4+0\cdot x^5+\cdots\\ (1+x)^4&=1+4\cdot x+6\cdot x^2+4\cdot x^3+1\cdot x^4+0\cdot x^5+\cdots\\ (1+x)^5&=1+5\cdot x+10\cdot x^2+10\cdot x^3+5\cdot x^4+1\cdot x^5+\cdots\\ &\vdots \end{aligned}

同刘徽一样，牛顿习惯采用实验归纳法。凭藉直觉，他设想 (1+x)^{1/2} 必定介乎 (1+x)^0 和 (1+x)^1 之间，于是列了一张表，将上式的系数抄录下来，期望通过内插法推得 r= \frac{1}{2} 该列的系数。

牛顿要猜出上表遗漏的部分，这有点像填字游戏或者我们小学里的找规律。先看第一行，无疑地，全部常数项的数值应为 1 。第二行 x 项的係数呈现等差数列 1,2,3,4,5 ，意味 (1+x)^r 中 x 项的係数应为 r 。再看第三行 x^2 项的係数 1, 3, 6, 10 ，牛顿知道这是这是等差数列求和 T_n=\frac{n(n+1)}{2} 。于是他猜测 (1+x)^r 中 x^2 项的係数应为 \frac{r(r-1)}{2} 。

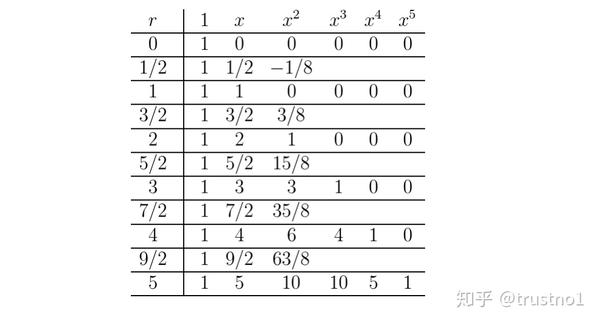
既然常数项是 1 ，x 项的係数是 r ， x^2 项的係数是 r(r-1)/2 ，那麽 x^3 项的係数应当为 \frac{r(r-1)(r-2)}{6} 。类似的推论可以持续进行， (1+x)^r 中 x^4 项的係数为 \frac{ r(r-1)(r-2)(r-3)}{4!} ， x^5 项的係数为 \frac{r(r-1)(r-2)(r-3)(r-4)}{5!} 。

牛顿按照这种规律逐一将表格补齐。从上表牛顿归纳出今人称之为广义二项式定理：

\displaystyle (1+x)^r=\binom{r}{0}+\binom{r}{1}x+\binom{r}{2}x^2+\binom{r}{3}x^3+\cdots

牛顿并没证明这个展开式。为了巩固他的“定理“。同刘徽在开方术中处理“朱幂”的一样，牛顿继续对猜想进行有限的倒算验证。譬如，比如他用 x^2 取代 x ， \displaystyle\begin{aligned} (1-x^2)^{1/2}&=1+\frac{1}{2}(-x^2)+\frac{\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)}{2}(-x^2)^2+\frac{\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)}{6}(-x^2)^3+\cdots\\ &=1-\frac{1}{2}x^2-\frac{1}{8}x^4-\frac{1}{16}x^6-\cdots \end{aligned}

他将上式等号右边平方，得到

\displaystyle\begin{aligned} &\left(1-\frac{1}{2}x^2-\frac{1}{8}x^4-\frac{1}{16}x^6-\cdots\right)\left(1-\frac{1}{2}x^2-\frac{1}{8}x^4-\frac{1}{16}x^6-\cdots\right)\\ &=1-\frac{1}{2}x^2-\frac{1}{2}x^2-\frac{1}{8}x^4+\frac{1}{4}x^4-\frac{1}{8}x^4-\frac{1}{16}x^6+\frac{1}{16}x^6-\frac{1}{16}x^6+\frac{1}{16}x^6-\cdots\\ &=1-x^2+0x^4+0x^6+\cdots \end{aligned}

经过这样有限个公式的验证牛顿认为这个公式可以适用于所有的有理数。无论是按照欧几里得的标准还是现代数学的标准，牛顿的这一宣称都是不可接受的，牛顿的二项式定理不能算是一个“定理“，只能算作“牛顿猜想“。然而牛顿并没有就此止步，他用这个猜测继续推进他的流术法

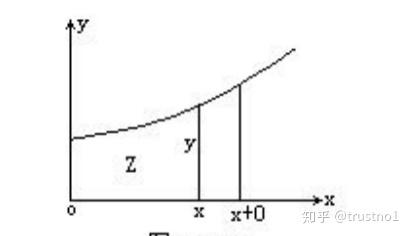
假设，坐标轴上一条曲线与坐标轴围成的面积是一个与x有关的m次的指数函数

z=ax^m ，在x轴上任取一点做垂线，然后再间隔一个无穷小增量o再做一个垂线

牛顿就得到了一个二项式 z+o\cdot{y}=a\cdot{(x+o)^m} ，牛顿对左边进行二项式展开得到

z+o\cdot{y}=a\cdot{(x^m+m\cdot{x^{(m-1)}}\cdot{o}+{\frac{m(m-1)}{1\cdot2}}\cdot{x^{(m-2)}}\cdot{o^2}+\cdots}）

由于 z=ax^m ，移项我们有

o\cdot{y}=am\cdot{x^{(m-1)}}\cdot{o}+a{\frac{m(m-1)}{1\cdot2}}\cdot{x^{(m-2)}}\cdot{o^2}+\cdots

然后两边除以o我们得到

{y}=am\cdot{x^{(m-1)}}+a{\frac{m(m-1)}{1\cdot2}}\cdot{x^{(m-2)}}\cdot{o^2}+\cdots

因为小于1的小数，经过高次幂运算后会快速趋近于0，因此o项的高次项都可以视同为0而被忽略掉，便得到了

{y^{'}}=am\cdot{x^{(m-1)}}

这里牛顿的无穷小量的定义和使用方法，与刘徽凭借直觉抹掉朱幂中“不足言之”的部分又有什么区别呢？牛顿没有办法证明，他这种把高次项抹掉的做法是逻辑自洽的。他在这里遗留下了一个困扰数学家几百年的逻辑漏洞——无穷小量到底是不是0？他在做除法的时候o不是0，在最终求值的时候o又是0。这就是第二次数学危机的核心论题。

如果我们比较一下，牛顿发明流术法和刘徽的求微数，我们可以发现两者诸多的相似之处。对于核心定理，刘徽没有给出无理数不可公度的证明，牛顿同样没有给出广义二项式定理的证明;对于核心的算法，刘徽对十进制渐进展开的余项收敛性猜测是收敛于0直接忽略，牛顿同样对流术法中二项式展开后的高次项的收敛值的猜测为0然后一抹了之.

在这两个核心问题上，刘徽和牛顿都地相信经验归纳法的直觉，而放弃了理性逻辑的证明。这一风格，不仅仅是牛顿独有的，而是牢牢占据了他死后两百多年的欧洲数学界。比如说，分析的化身欧拉，在他的著作中所使用的各种无穷级数都是没有严格证明过收敛性的，然而他却凭着自己惊人的直觉，自由的操纵这些数学工具。在没有严格证明的情况下，微积分在近两百年里在整个欧洲广泛传播使用，成为了所有理性学科的奠基石。这其中最直接的理由，就是微积分的计算价值实在太广泛了，从物理到土木工程，从天文到经济，这个技术就如热刀切黄油一样解决了无数问题。既然好用，那么无穷小到底是个什么鬼，有那么重要吗？对于数学家的内心很重要，但是对于数学工具的使用者而言没有那么重要。然而正是这些计算的广泛应用，为理论数学家们获得了无数可以广泛研究的素材。天文航海观测极大刺激了插值法的研究既而催生了泰勒级数，欧拉研究流体力学第一次引入微分方程，傅立叶在热传导研究中获得傅立叶变换。正是这样经过几百年的反复积累，柯西的现代极限理论不过只是水到渠成的必然结果而已。

罗马不是一天建成的，数学的大厦也不是脱离我们意志天然地耸立在哪里，只等着我们人类中某一位智者灵光一闪去发现他们。逻辑演绎的确是数学大厦拔地而起的基石，然而在数学大厦拔地而起之前，数学家们需要构建起一层层的外周框架。在此基础上数学家需要不断层累各种粗糙原始的数学成果。当数学成果积累到一定的程度时，数学家才能从这些数学实体中抽象出共有的数学特性，将前代的知识打碎重装再整理，形成更精致的数学体系。

严格性在人类整理数学知识方面起到无可比拟的作用，然而数学的发展并非是以严格性为前提条件的。有足够的数学成果积累才是前提，在许多数学理论的早期蓬勃发展的数学方法都是与各种是是而非的猜测猜想为伴。中国数学家对数的研究依托于有限归纳下的朴素的直观。这种有限归纳的朴素直观，恰恰是所禁止的。如果我们能够接受牛顿以这么不严谨的方式创立学说作为微积分的开端，那么我们又该如何去看待中国传统数学呢？