谢邀，圆锥曲线为什么叫「圆锥曲线」？因为椭圆、圆形、双曲和抛物都是平面和一个圆锥相交的不同结果：

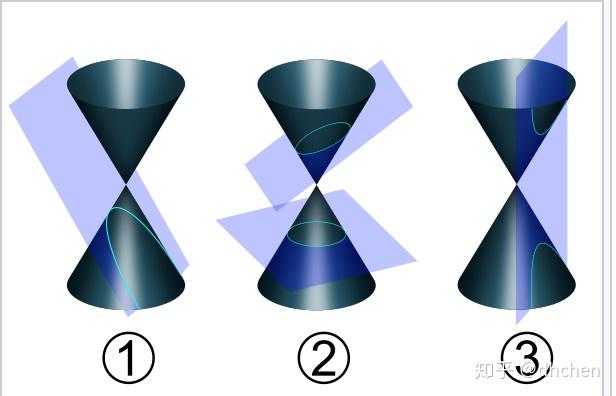
这就是古人最早研究这类曲线的基本起点。古希腊的数学家Apollonius of Perga被认为是最早发现他们的人. 然后是Menaechmus，它利用圆锥曲线解决了二倍立方体的问题（当然了，这超过了尺规作图的范畴)。

二倍立方体就是给定一个立方体构成一个体积恰好是这个立方体两倍的立方体。按照现代的数学语言就是构造 x^3=2 的解。古希腊其他数学希望用圆规和直尺（无刻度）来搞定它们，结果做不出来。然后Menaechmus笑了笑，它弄出来了一个抛物线和一个双曲线（实际上就是 x^2=y, \,\, xy=2 ）然后他们的交点自然就是解了。

在发明坐标系前，数学家一般通过纯平面几何定义的方式来研究椭圆、双曲线和抛物线。比如椭圆就是到两定点的距离和为固定值的曲线。1602的时候开普勒发现火星的轨道应该是一个椭圆（太阳就在椭圆的一个焦点）。这也是圆锥出现最重要的一个应用。 然后哈雷发现哈雷彗星也是一个椭圆。

确定圆锥曲线的坐标表达是非常简单的，甚至可以这样说，它们是发明坐标系后的首批结果。笛卡尔大神(1596-1650)在发明坐标系后首先干的一件事就是在坐标系下研究了圆锥曲线, 也就是基于解析几何的观点研究圆锥曲线。 时间点也远远早于「近代」，明末清初的时间。你认为高端的东西其实发现的时间比你想象得早，牛顿、莱布尼茨搞微积分的时间是在清朝。

当然了，笛卡尔那个时候的坐标系还是和现在的不太一样的，具体可以看下面的文献。

Classification of a curve in the style of Descartes