在我们日常生活和学习中，二次曲面无处不在。无论是自然界的物体形状还是计算机图形学中的虚拟世界，都离不开这个重要的数学概念。了解二次曲面的定义、方程表达式和应用可以让我们更深入地理解它们在现实世界中的重要性。本文将带您一起探索二次曲面的奥秘，揭示它们在工程学、计算机图形学和数学研究中的精彩应用。

一、二次曲面的定义及方程表达式

二次曲面是三维空间中的一类曲面，其方程可用二次方程表示。我们可以将二次曲面的方程表达式写为：

Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0

其中，A、B、C、D、E、F、G、H、I、J 是常数，且至少有一个系数不为零。

例如，考虑方程 x^2 + y^2 + z^2 = 1，这是一个简单的二次曲面方程，表示了一个单位球面。在该方程中，A、B、C 的系数都为 1，而其他系数为零。

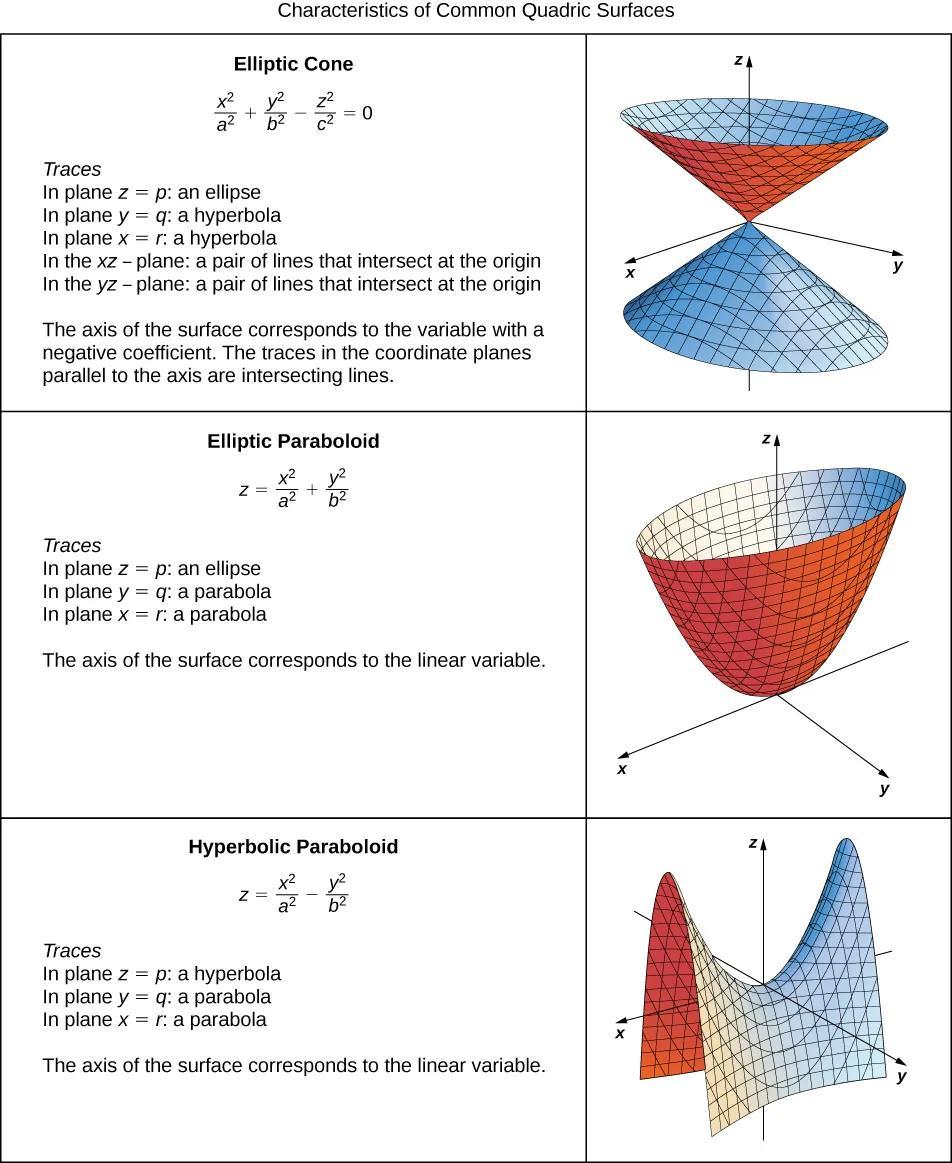
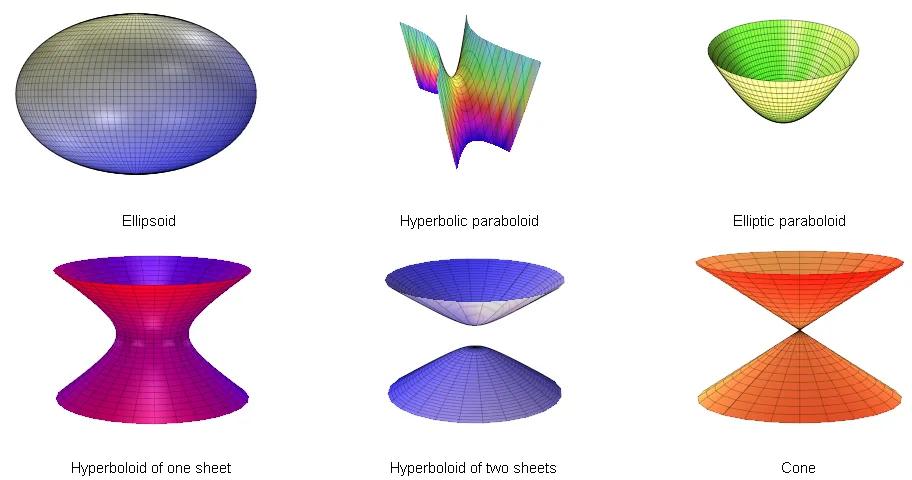
二次曲面示例

二、不同类型的二次曲面

a) 椭球面

椭球面是一种常见的二次曲面类型。当 A、B、C 的系数都大于零时，二次曲面呈现为椭球面。椭球面可以描述物理学上的椭球体、行星轨道等。例如，方程 (x^2/a^2) + (y^2/b^2) + (z^2/c^2) = 1 描述了一个具有不同半轴长度的椭球面。

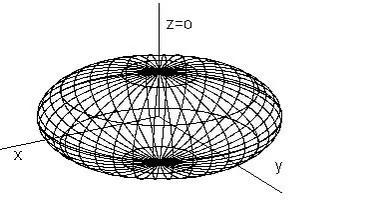
b) 双曲面

双曲面是另一种常见的二次曲面类型。当 A、B、C 的系数中至少有一个大于零，而另外两个小于零时，二次曲面呈现为双曲面。双曲面在光学、电磁学和天体力学等领域具有重要意义。例如，方程 x^2/a^2 - y^2/b^2 + z^2/c^2 = 1 描述了一个双曲抛物面镜。

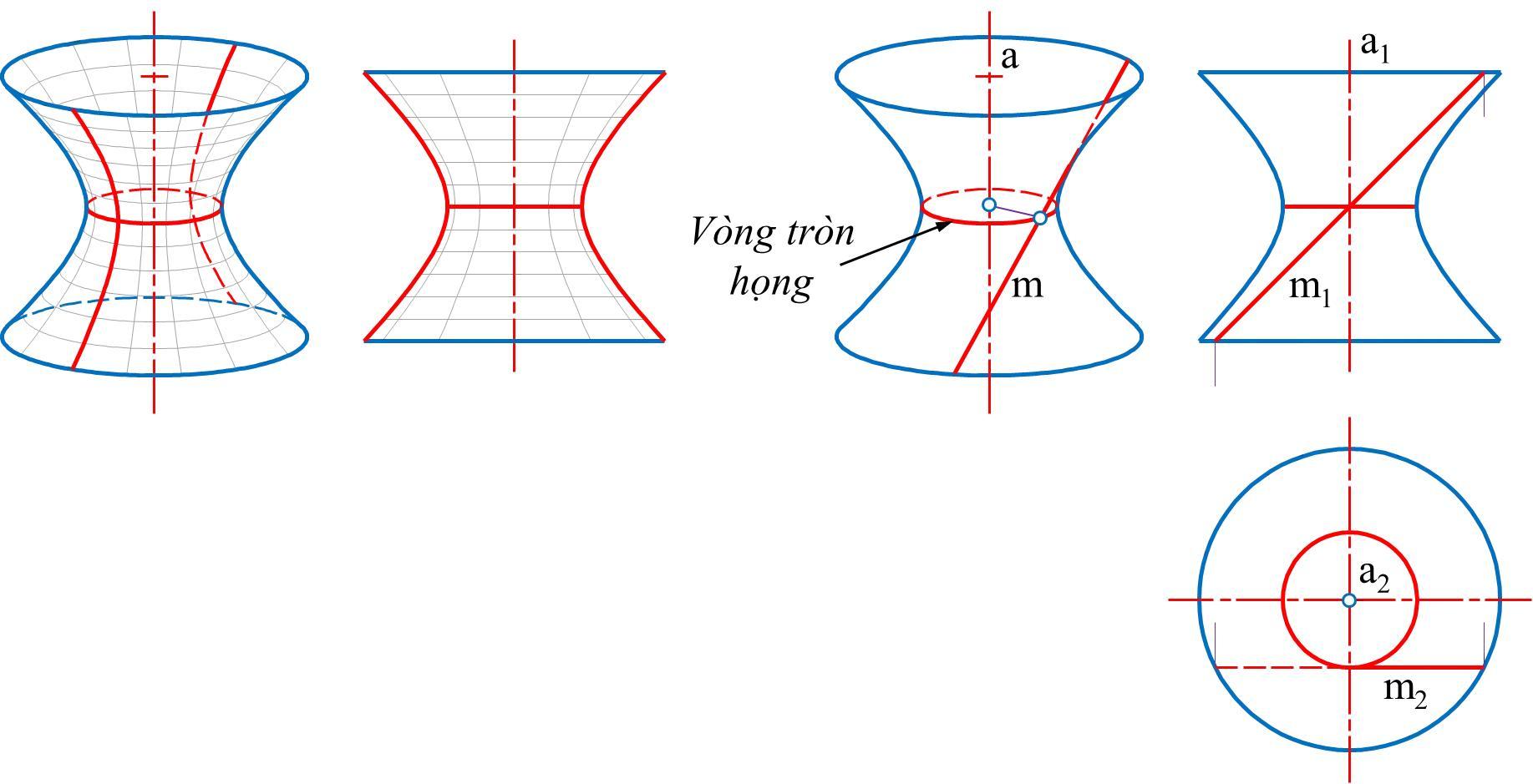
c) 抛物面

抛物面是另一类常见的二次曲面类型。当 A、B 的系数中有一个为零，而另一个不为零时，二次曲面呈现为抛物面。抛物面在物理学和工程学中广泛应用。例如，方程 x^2/a^2 + y^2/b^2 = z 描述了一个抛物面，用于描述自由落体的轨迹或者抛物线天线的信号范围。

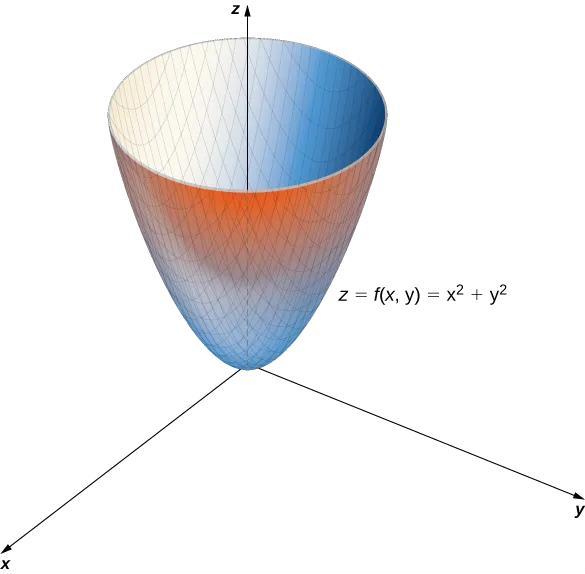
三、二次曲面的应用

a) 工程学中的应用

二次曲面在工程学中有广泛的应用。例如，在声学工程中，通过二次曲面来建模声音的传播和反射，以优化音响系统的设计。在电磁学中，二次曲面可用于描述电场和磁场的分布，对天线的指向性进行分析和优化。流体力学中，二次曲面可以描述流体的流动和压力分布。

b) 计算机图形学的应用

二次曲面在计算机图形学中具有重要应用。通过对二次曲面的变换、插值和渲染，可以创建出逼真而华丽的图像效果。例如，在汽车设计中，使用二次曲面来建模车身曲线和表面细节。在动画制作中，利用二次曲面来建模人物角色的身体曲线和面部特征。

c) 数学推理与研究

二次曲面作为数学研究的重要领域，涉及到代数几何、微分几何和偏微分方程等多个数学分支。深入研究二次曲面的性质，有助于发展数学理论，并提供了基础概念和工具，用于解决更广泛领域的问题。二次曲面的研究还可以帮助解决最优化问题和约束问题。

结语

通过了解二次曲面的定义、分类和应用，我们能够更好地理解数学在自然界和人工环境中的应用。无论是实际工程中的建模和优化，还是计算机图形学中的创造和渲染，二次曲面都发挥着重要的作用。同时，深入研究二次曲面的性质也丰富了数学理论，并为其他学科的发展提供了基础。让我们一同探索二次曲面的奇妙之处，感受数学的无限魅力。