半个月前学习到了圆锥曲线，看到高中练习册中繁杂的计算，心中便烦了起来：圆锥曲线本应是几何内容，却被参考答案用代数解析的方式硬生生的变成了代数问题。

于是我便开始发明几何方法解题。

几何的难点在于很难想到，但是想到解法之后计算量可以说是几乎没有。

下面开始正题。

其实这个方法并不是很难想到，当我发明出这个方法的时候也并不是用了许久，而是在这之后也是看到知乎中的答案才知道这个叫做仿射变换。

首先我们来看一下椭圆：

这是椭圆 \frac{x^2}4+\frac{y^2}3=1 的图像。

不过椭圆方程并不重要，我们今天要讨论的重点是几何问题，而不是代数问题。

一、圆与椭圆

一个椭圆有三种定义：

① 一个圆被均匀拉伸得到的是椭圆。

② 一个斜面与圆锥的交线若闭合，则为椭圆。

③ 满足到两个定点的距离之和为定值的点的集合为椭圆。

至于怎么证明这三个定义是等价的就不详细说明了，可以去看看3blue1brown的视频：

【官方双语】数学天赋是什么样的？它从何而来？（丹迪林双球）_哔哩哔哩_bilibili

本文只关心第一个定义。

如果我们能把一个椭圆拉伸一下，把它变成圆，那么是不是会简单许多呢？

因为圆有很多性质是椭圆不具备的，通过这样的变换，是否可以让椭圆变得更简单些呢？

答案是：是的，有些特殊情况下甚至可以把两页的标准答案变成一个二次方程就能解决的问题！

其实根本原因就在于某些题目就是根据这个背景来出的，所以非常好用。

具体案例我们最后在讲，我们现在要做的是统一一个模型，找出在椭圆中通用的方法。

首先，一个椭圆有四个顶点，而四个顶点的坐标分别对应方程中的 a 和 b 。

所以我们可以将整个坐标系的所有点的横坐标缩小到原来的 \frac1a ，纵坐标缩小到原来的 \frac1b ，也就是说，如果我们这样变换的话，椭圆就变成了一个单位圆！

而且我们会得到一个性质：我们看椭圆的焦点 F( c , 0) ，在经过变换之后变成了 F'(\frac{c}{a},0) ，也就是说经过变换之后 F 的横坐标是椭圆的离心率！

不过这个用处不大，因为变换到圆之后离心率的意义就不大了。

好，那让我们看一看变换之后哪些东西发生了改变。

二、变换

由于此小节是关于变换的，下面的结论是非常通用的结论，椭圆只是给我们提供怎么变换，此小节不会涉及到椭圆。

1.面积

对于一个图形来说，它的面积肯定是改变了的。我们先看一个长方形：在经过变换之后，它的长缩小了 a 倍，高缩小了 b 倍，所以它的面积会缩小到原来的\frac1{ab} 。

其实这对任何图形都是有效的，对任意图形进行这种变换面积都会缩小到原来的 \frac 1{ab}

同理，有时候我们需要把圆放缩回椭圆来求原位置的面积，此时就应该乘以 ab 。

注：其实这是线性代数的知识，如果你了解线性代数的话，你应该可以知道，这种变换便是矩阵 A= \begin{bmatrix} \frac1a & 0 \\ 0 & \frac1b \end{bmatrix} ，其行列式便表示了面积的数乘大小，即 \det A = \frac1{ab} 。

2.斜率

如果横坐标和纵坐标拉伸的不一致，那么斜率便会变化，这是肯定的。

在此变换中，我们假定一条线AB

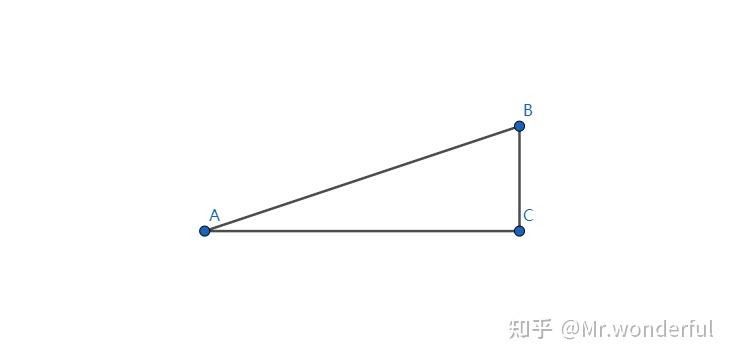
AC与BC分别平行于x轴和y轴

我们设 AC=n, BC=m ，那么直线斜率为 \frac{BC}{AC}=\frac mn

我们做了变换之后，由于变换同时对坐标的两个参数(x和y)生效，所以在平行于x轴和y轴的线段的长度只受一个缩放影响，也就是说， AC 长度变换后为 \frac na ， BC 长度变换后为 \frac mb ，所以变换后直线斜率为 \frac{\frac mb}{\frac na} = \frac mn \cdot \frac ab

也就是说，变换过程中会将一条线的斜率乘以 \frac ab 。

如果要从圆变回椭圆的话，应当乘以 \frac ba 。

3.线段长度

对于任意线段 AB ，在变换过程中，长度肯定是要变化的。

我们不妨把 AB 写成向量： \overrightarrow{AB} (x,y) ，则 \left| \overrightarrow{AB}\right| =\sqrt{x^{2}+y^{2}}

变化后的 \overrightarrow{AB} 记作 \overrightarrow{AB} ^{T}(\frac xa,\frac yb) ，则 \left| \overrightarrow{AB}^{T}\right| =\sqrt{\left( \dfrac{x}{a}\right) ^{2}+\left( \dfrac{y}{b}\right) ^{2}}

两边平方得： \left| \overrightarrow{AB}^{T}\right| ^{2}=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}

注意到了嘛？对于任何向量 \overrightarrow{AB} (x,y) ，把坐标带进椭圆方程便是变换后的长度。

同理，对于变换后的向量 \overrightarrow{AB}^{T}\left( x,y\right) ，变换回椭圆之后的长度 \left| \overrightarrow{AB}\right| ^{2}=a^{2}x^{2}+b^{2}y^{2} 。

而从上面的式子不难看出，长度变换是不成线性关系的。也就是说，长度变化不止和原来的长度有关系，即使两条线段原长相等，若是斜率不同，变换后所得的长度也是不同的。

而这也提醒了我们，我们可以用另一个公式表示线段长度与线段变换后的长度。既然斜率会影响长度变换，那么我们的式子里面应该会有斜率 k 存在，而且应该可以仅仅通过 k 就能确定原长和变化后长度的关系。所以，我们的式子应该为 \left| \overrightarrow{AB}^{T} \right| = \left( 某个带k的式子 \right) \cdot \left| \overrightarrow{AB} \right|

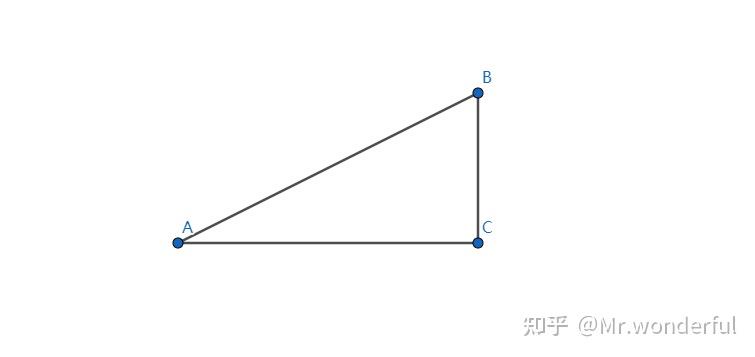
AC与BC分别平行于x轴和y轴

还是这幅图，我们设 AB 的斜率为 k ，易得

\dfrac{BC}{AC}=k \quad AB^{2}=AC^{2}+BC^{2}

所以有 AB^{2}=AC^{2}+k^{2}AC^{2}

即 AB^{2}=\left( 1+k^{2}\right) AC^{2}

所以对于变化后的 AB^{T} 可得： \left( AB^{T}\right) ^{2}=\left( 1+k^{2}\cdot \dfrac{a^{2}}{b^{2}}\right) \cdot \dfrac{AC^{2}}{a^{2}}

两式相除，化简得： \left( AB^{T}\right) ^{2}=\dfrac{k^{2}a^{2}+b^{2}}{\left( 1+k^{2}\right) a^{2}b^{2}}\cdot AB^{2}

这便是我们的另一个公式，这个公式稍显复杂，其实用处也不是特别大，因为对于长度来说在进行变换时并不是一个线性变换，所以在解决长度问题时一般不使用仿射变换的方法，如果硬要带入的话也可以，不过又变成了一个硬生生的代数问题了。

三、用圆观察椭圆1.形如 \frac {x^2}{a^2}+\frac {y^2}{b^2}=\lambda 的椭圆离心率相等的解释

细心的读者可能在上节已经发现了一些东西了，比如说，对于任何向量 \overrightarrow{AB} (x,y) ，把坐标带进椭圆方程便是变换后的长度，于是对于椭圆方程 \frac {x^2}{a^2}+\frac {y^2}{b^2}=1 ，假设 P 是椭圆上一点，那么 \overrightarrow{OP} 变换后的长度就恒为1，表示椭圆变换后是一个单位圆。如果右边的数字不是1呢？如果是别的数字 t 的话，那么说明变换之后不是单位圆，但也是一个圆，是一个半径为 \sqrt t 的圆。所以说，不管右边是什么数字，它的长轴与短轴之比应该是固定的，也就是说对于 \forall t\in \mathbb R^+ ，椭圆 \frac {x^2}{a^2}+\frac {y^2}{b^2}=t 的离心率相等。这也是椭圆最基本的性质之一。

2.椭圆中的垂径定理——中点弦

在圆中最常用的定理便是垂径定理：圆的任意一条弦的垂直平分线过圆心。

也就是说，取任意一条弦以及它的中点，这条弦与中点和原点连接的线段斜率乘积为 -1 （即两条线垂直）。

于是，在圆变化到椭圆的过程中，由于两条线的斜率均会乘以 \frac ba ，所以

在椭圆中任取一条弦与这条弦的中点，这条弦的斜率与中点和原点连线的斜率乘积为 -\frac {b^2}{a^2} 。

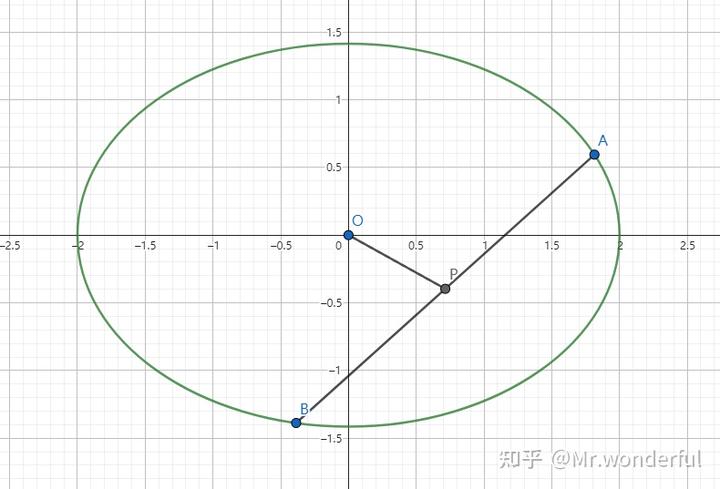
k_{AB}\cdot k_{OP} = -\frac {b^2}{a^2}\\

3.椭圆中的圆周角

在圆中，有一个非常重要的性质：直径的圆周角是直角。

也就是说，对于圆的任意一条直径，在圆上另找一点，这一点到直径两边连线的斜率乘积为 -1 （两线垂直）。

如果变换到椭圆，和上一条结论一样，我们便可以得到一个结论：

在椭圆上取任意关于原点对称的两点 A B ，与椭圆上另外一点 P 连线的斜率之积为 -\frac {b^2}{a^2}

k_{PA}\cdot k_{PB}=-\frac {b^2}{a^2}\\

4.浅谈数学中的发明

前面的例子只是证明了很少一部分性质，其实仿射变换能够解决的问题非常之多，对于前面的例子只是一个引入，在这里作者鼓励大家去发明更多的，更加有意思的，更加美妙的证明方法与结论。我们的目标是在本质上理解一个工具，了解它是如何发明的，又为何能够想到这些，才能够让我们从更底层的层面去使用，去扩展它们。就像读前文的时候，应该有人会问道：为什么两条线垂直我们就可以得到这些结论呢？那圆的任意一个弦的圆周角都是固定的呀，为什么不去扩展其他情况呢？问出这种问题的读者，是我要夸赞的读者，有扩展思维的人会想尽办法将许多看似有关联的东西集合成同一个模型。其实只要有关联的话，确实可以化作同一个模型，就像刚才提出的问题一样，如果思考这个问题的话，我们就会发现，同一个角旋转后斜率乘积是会变化的，只有直角才能保持斜率乘积为 -1 这种奇妙的性质。所以我们研究直角才可以这么轻松。

有时候性质和定理往往是从一个问题演变出来的。看到一个性质或定理，问一问：在这个性质或定理的前提之外是否还存在更普遍的结论呢？这个定理是不是在这一定义下是那个更普遍结论的特殊情况呢？这往往有奇效。

其实聪明的读者会发现第二节的内容有面积、斜率、线段长度三种变化，却好像少了一种，那就是角度。但是因为角度变化就是用斜率变化计算的，有兴趣的读者可以尝试自己推导一下变换公式（ \enclose{horizontalstrike}{绝不是我自己懒不想推} ）。

（好吧让我先咕一会，这个公式一想就应该长得应该不怎么和谐）

自此，我们的前置知识就全部到位了，我们来上几道题试试手吧，相信我，你马上就会感受到秒杀的快感。

四、例题

大题的第一问往往是求椭圆方程，非常简单，所以下面的题目我会把第一问省略，直接开始第二问或者第三问。

1.较为明显的中点弦

过点 M(1,1) 作斜率为 -\frac12 的直线与椭圆 b>0)">C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 相交于 A B 两点，若 M 是 AB 的中点，则椭圆的离心率为__________.

解：我们把椭圆放缩成了一个单位圆，所以 M 应当变为 M'(\frac1a,\frac1b) ，直线斜率应当变为 -\frac12\cdot\frac ab=-\frac a{2b} ，而 OM' 的斜率为 \dfrac{\frac1b}{\frac1a}=\frac ab 。而这两条线应当垂直，所以有 -\frac a{2b}\cdot\frac ab=-\frac {a^2}{2b^2}=-1 ，因此 \frac{b^2}{a^2}=\frac12 ，所以 e=\frac{\sqrt2}{2} 。

2. 稍稍隐藏的中点弦

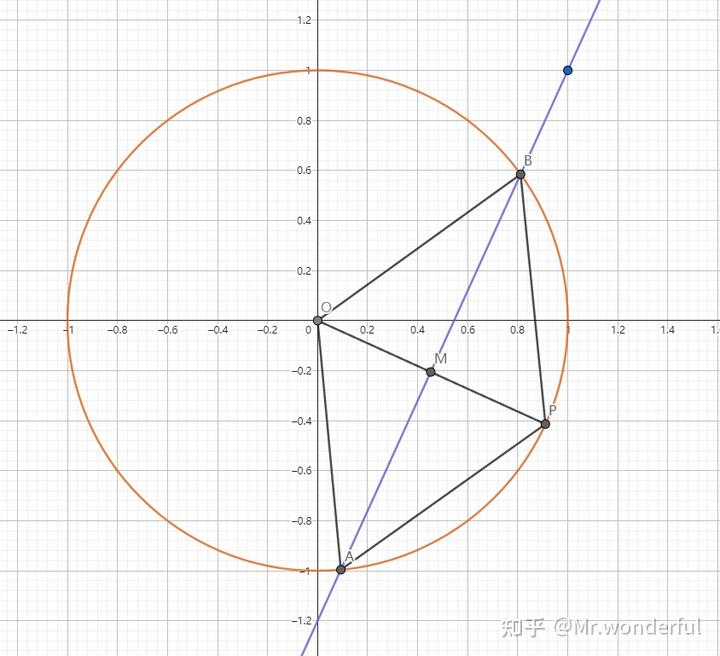
在椭圆 C:\frac{x^2}4+\frac{y^2}3=1 中，一条直线 y=kx+m 与椭圆交于 A B 两点，同时椭圆上有另一点 M

，若 \triangle ABM 的重心为坐标原点 O ，求 \triangle ABM 的面积。

解：此题条件可以直接转化为：在椭圆上任取不重合的三点构成的三角形的重心在坐标原点，求面积。

我们发现，重心是三条中线的交点，而这有过坐标原点，这不是妥妥的中点弦嘛！于是我们考虑放缩：

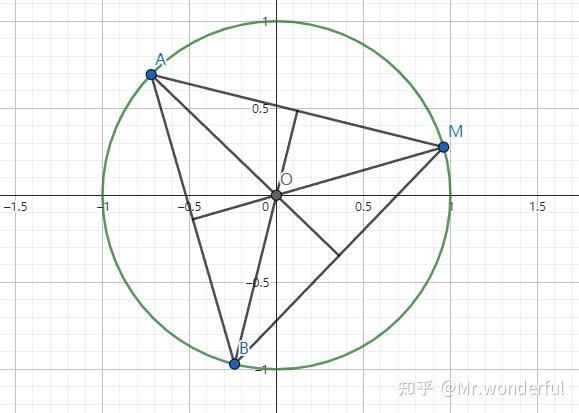
变换后的单位圆

将椭圆放缩成单位圆，那么我们就会发现，此时 \triangle ABM 的重心是坐标原点，说明每条边的中线过原点，而原点与中点的连线与边垂直，那么说明每条边的中线就是垂线，所以，此时 \triangle ABM 为正三角形！

因此，单位圆中的正三角形面积为 \frac{3\sqrt3}{4} ，考虑到已经放缩，把它变换回椭圆之后的面积为 \frac{3\sqrt3}{4}\cdot2\sqrt3=\frac92 。

简单吗？让我们来看看参考答案是怎么做的。

3.更深一层的中点弦

已知椭圆 0)">C:9x^{2}+y^{2}=m^{2}( m > 0) ，直线 l 不过原点 O 且不平行于坐标轴， l 与 C 有两个交点 A ， B ，线段 AB 的中点为 M 。若 l 过点 (\frac m3,m) ，延长线段 OM 与 C 交于点 P ，求当四边形 OAPB 成为平行四边形时 l 的斜率。

解：先把图画出来吧，我们可以清晰地看到有两种情况满足题意。（画图时按照 m=1 画的，不过 m 是几不重要，因为相当于把横轴和纵轴等比放缩了，斜率不变）

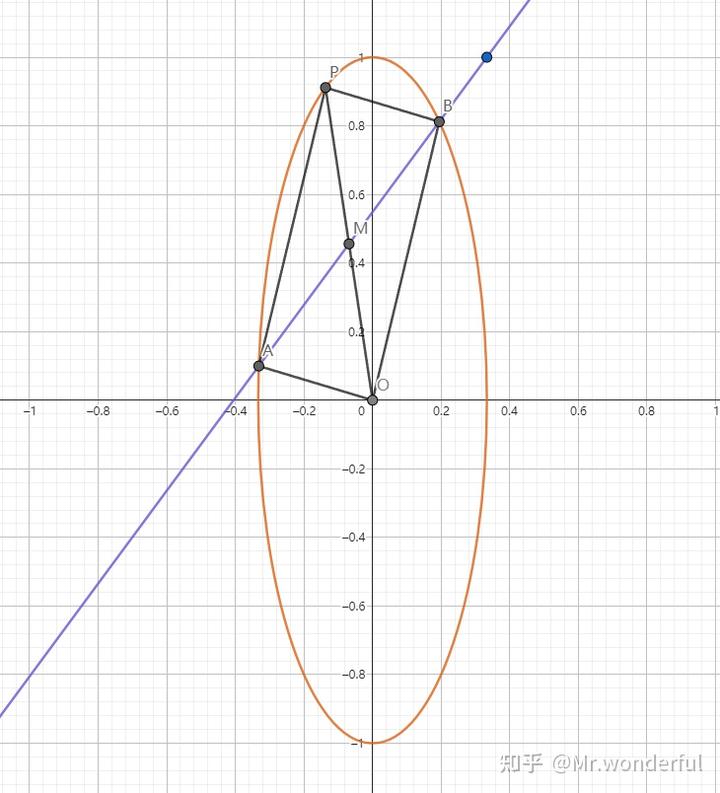
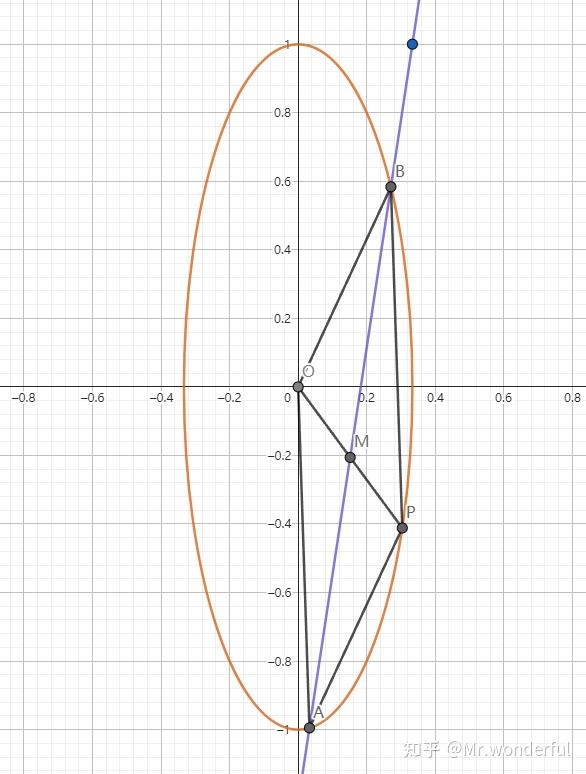
此时我们需要想到一个性质，那就是我们的变换对斜率来说是线性的，也就是说，变换前平行的两条线变换后仍然平行。不平行的两条线变换后仍然不平行。于是，我们可以理所当然的把它变换成一个圆解决问题。

那么这个方法在这道题中好用吗？我们观察一下：一个四边形要是平行四边形，那么它的对角线应该是相互平分的，而它的一条对角线 AB 正好就是椭圆的一条弦，于是我们得到了中点弦！开整！

但此时我们不能按照原来的变换了，因为椭圆方程里面本身就含有 m ，那么，我们是否可以直接化成一个半径为 m 的圆呢？

当然可以。因为原方程为 9x^{2}+y^{2}=m^{2} ，那么我们只需要将 x 轴放大3倍，就得到了一个半径为 m 的圆。

另外一种情况通过代数运算也是一样的，所以这里只画一种情况

此时变换后的方程为 x^2+y^2=m^2 ，我们发现： OM\perp AB 且 OM=\frac m2 ，此时 AB 过的定点为 (m,m)， 那么我们直接设 AB:y-m=k(x-m) ，使得原点到直线的距离为 \frac m2 就行了。

于是我们有 \dfrac{\left|(1-k)m\right|}{\sqrt{k^2+1}}=\dfrac m2

解得 k=\dfrac{4\pm\sqrt7}{3}

所以变换回椭圆时， k=4\pm\sqrt7

来看看参考答案的长度吧：

五、深度拓展

这一章主要来对上文3.4小节做一个续写吧，我及其鼓励大家去探寻一些新的方法，扩展新的前提。

打个比方，我希望我的读者在看完前面的内容会想到一个问题：这些都是椭圆里面的内容啊，那抛物线和双曲线呢？你的题目叫做圆锥曲线，可是你这种应用好像只适合椭圆啊！

那双曲线呢？按照这个思路，我能不能把它拓展到双曲线呢？

如果你能想到这个问题，那么作者会非常赞赏你，或许你可以先不要看下面的内容，先自己想一想，看看能不能想到一些拓展。

就拿双曲线举例子，我能否将双曲线转化一下呢，既然我可以把椭圆放缩成圆，那么我可不可以把双曲线转成椭圆呢？

让我们先来简单发明一下吧。

我们只看双曲线的一支，就比如左支。

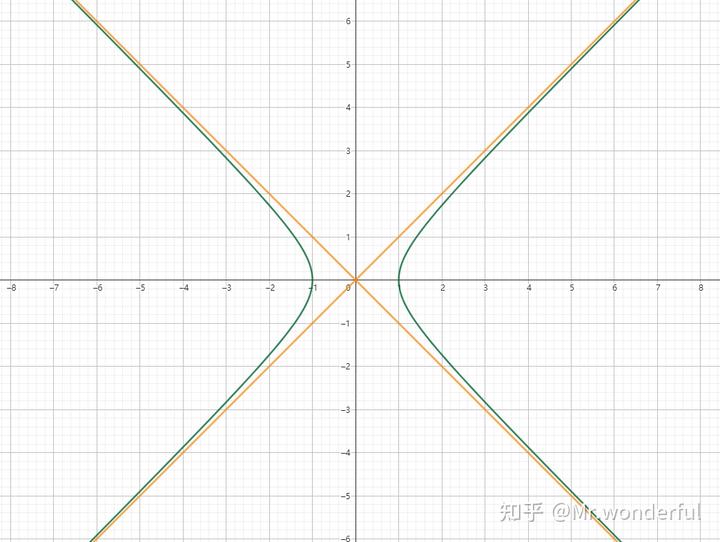
如果我无限把视角往左边移动，那么双曲线会与渐近线越来越近，那么我们考虑一下，有这样一个点，它距离我们无穷远，它的横坐标非常小，小到无论我们怎么往左边看也看不到这个数字。那么既然这个点比我们无论怎么想象都更靠左边，而且既然双曲线会与渐近线越来越近，那么我们就可以说：双曲线在这个位置上和渐近线相切。而且我们给这个点起个名字吧，就叫它无穷远点好了。

那么我猜你会问：既然它是个点了，那么就算你说的是对的，那也应该有两个切点啊，怎么可能只有一个位置呢？

这其实是个误区。我们假设这个平面上有两点 P， Q ，还有一个无穷远点 n_\infty ，我们首先应该假设这个无穷远点是哪一个无穷远点，比如说它的纵坐标无限大和横坐标无限大，显然一个在上面，一个在右面，肯定是不一样的。我们定义这个是横坐标无限大的点吧。我们可以尝试写一下： n_\infty=\lim _{x \to \infty}(x,0)

那么我们先假设这个无穷远点不在无穷，我们让它动态的前往无穷。

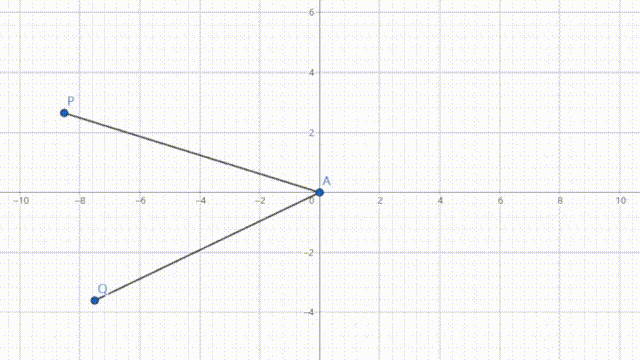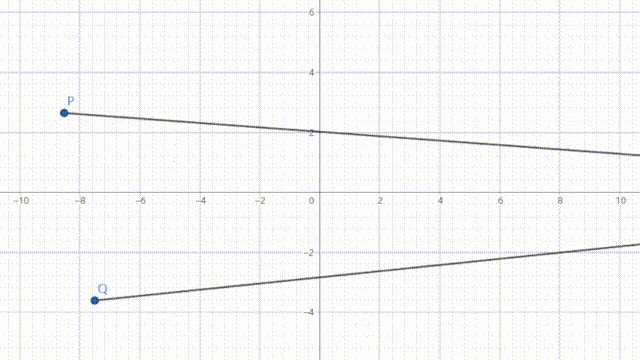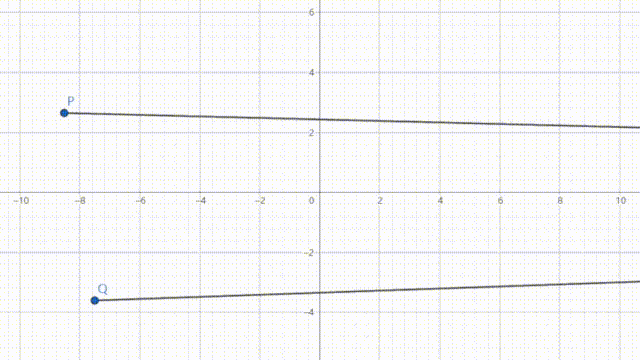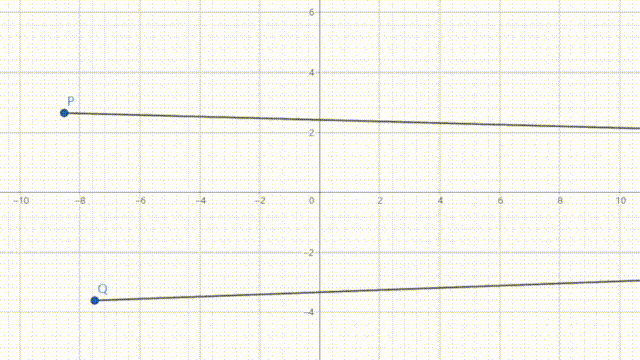
我们可以看到， Pn_\infty 和 Qn_\infty 的斜率都逐渐趋于0，所以说，任意两点和无穷远点的连线平行。

也就是说，无穷远点其实不只是一个点，应该是一条线。

比如，这两个无穷远点应该是等价的： n_\infty=\lim _{x \to \infty}(x,0) 和 n_\infty=\lim _{x \to \infty}(x,1)

其实，上面举的这些例子让我们已经踏入了一个新的领域：射影几何。我相信在这里你已经感受到了发明一种数学的美妙，上面的例子只是射影几何最基础的部分，而且我希望大家可以保持住对数学的这种新鲜感，去发明，去创造。

2023.2.8更

其实仿射变换不仅可以研究中点弦，只是中点弦比较容易思考而已，真正的仿射变换和几何学连结在一起的力量是无穷的，近期看到一篇文章给大家分享一下，非常巧妙。