SCI论文（）

摘要:圆锥曲线中的距离与弦长问题是历年考试的热点，也是高三复习备考中的重点专题.结合个人的教学现状，从对距离公式的理解到公式的系统总结和应用，谈谈自己的教学建议与策略，倡导在深度学习中提升学生的核心素养.

关键词:深度学习;距离;弦长;核心素养

2022年的高考数学试题精彩纷呈，备受关注.教育部考试中心指出:“试题落实立德树人根本任务，促进学生德智体美劳全面发展，体现高考改革要求;试题突出数学学科特点，强化基础考查，突出关键能力，加强教考衔接，服务‘双减’政策实施，助力基础教育提质增效．”笔者研究学习过后，深受启发．随着“新课标、新课程、新教材、新高考”改革的不断推进，笔者认为我们老师只有带领学生一起“深度研究”“深度学习”，培养学生的高阶思维，才能提升学生的数学素养，迎接新的挑战．下面以圆锥曲线中的距离与弦长问题为例，结合高考真题，谈谈自己的教学感想与策略.

1对距离公式的错误认识

急功近利的思想经常让老师和学生只顾公式、定理的应用，却不愿意去“深度理解”背后的原理，导致一知半解就去进行“题海战术”的训练，最终事倍功半.

2直线方程的设法与距离公式的选择

在直线和圆锥曲线的综合问题中，我们经常要选择合适的直线方程形式来减少计算量．一般地，若

选择不同的直线形式，对计算量影响很大，这一点可以在教学实践中，让学生通过例题对比、发现、感受，老师再提炼总结，帮助学生优化解题路径.

3在不同的问题情境中选择最恰当的距离公式

与距离和弦长有关的圆锥曲线问题往往情境复杂，加上公式的多样性会导致学生不知道如何选择，一旦选择不好公式，则会陷入极其复杂的计算，所以教会学生如何在不同的问题情境中识别问题的本质，根据已知条件，选择最佳解题方案，也应该成为“深度教学”的一部分．下面举例说明.

4二级结论的推导、记忆与甄选

学生往往缺乏理智的判断，喜欢投机取巧，在网络上学习各种“秒杀法”，背诵各种二级结论．比如

然后在平时的训练或是考试中就套用死记硬背的结论，结果一次又一次地丧失训练计算能力的机会，一旦遇到新的问题情境便束手无策.

笔者认为，立足教材，推陈出新，“自然生成”各种二级结论，带领学生一起深度研究各种结论的发生发展过程，既能在训练中潜移默化地提升数学素养，又能满足学生急于摄取二级结论的需求，可谓一举多得.

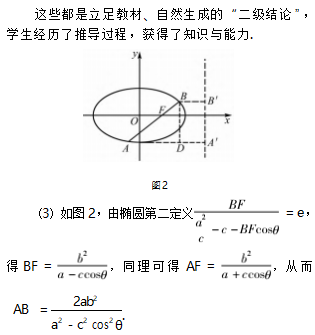
小结立足教材的二次开发与利用，可以推出很多新的结论，让各种二级结论有本可依，而不是让学生死记硬背，重点是我们老师要引导学生在深度研究中获得知识与能力，让核心素养自然生成．以上研究历程可以迁移到双曲线和抛物线中，读者可以自行尝试.

5深度总结，系统归纳

从直线方程开始，到圆、椭圆、双曲线、抛物线，与圆锥曲线的弦长和距离有关的知识和习题都是散布在教材的各个角落，学生初学圆锥曲线时，我们不可避免地要让他们进行碎片化的学习，但在学完以后，我们老师应该引导学生进行“大单元”归纳，“专题式”总结，深度研究过后的系统归纳很有必要，帮助学生形成丰富的网状结构更有利于学生在应对新问题时，可以快速提取，高效解题．以椭圆的右焦点弦为例，有如下公式可以选用.

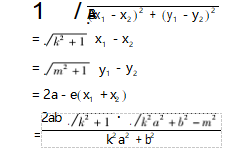
所以笔者认为，二级结论本身没有错，错的是不讲原理直接生搬硬套．我们老师要做好学生的引路人，在日常教学中要带领学生一起继续深度研究、深度学习，在学生能够接受的前提下不断深挖教材，讲清知识的来龙去脉的同时让学生见多识广，才能让学生从中获得系统、全面的知识，让核心素养落地生根．笔者只是以椭圆弦长为例，系统总结了各种公式，可以让学生用同样的方法去研究抛物线和双曲线，学生在研究过程中所形成的能力，远比知识本身重要得多．学生在研究过程中所提升的计算能力以及锤炼的坚强毅力，是他们在考场上乃至未来的学习中攻坚克难的保障.

参考文献:

［1］梁敏聪．高中数学深度学习教学策略的研究［J］．新课程，2022(16):80－81.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！