在和文章中，我们详细介绍了主成分分析(PCA)的分析方法、结果解读和可视化。此篇文章我们将介绍探索性因子分析(EFA)的分析流程。

本章包含以下内容：

1) 数据探索；

2) 确定提取因子数目；

3) 因子旋转；

4) 探索性因子分析结果可视化；

5) 回归模型构建。

一、数据探索

此数据为虚构，可用于练习，请不要作他用。

1.1数据导入

# 1.1.1 设置工作路径#knitr::opts_knit$set(root.dir="D:\\EnvStat\\PCA")# 使用Rmarkdown进行程序运行Sys.setlocale('LC_ALL','C') # Rmarkdown全局设置#options(stringsAsFactors=F)# R中环境变量设置，防止字符型变量转换为因子setwd("D:\\EnvStat\\PCA")
# 1.1.2 数据导入data <- read.csv("env.csv", header = T, row.names = 1)dim(data)## [1] 36 14head(data) # 3个分类变量，11个数值变量。

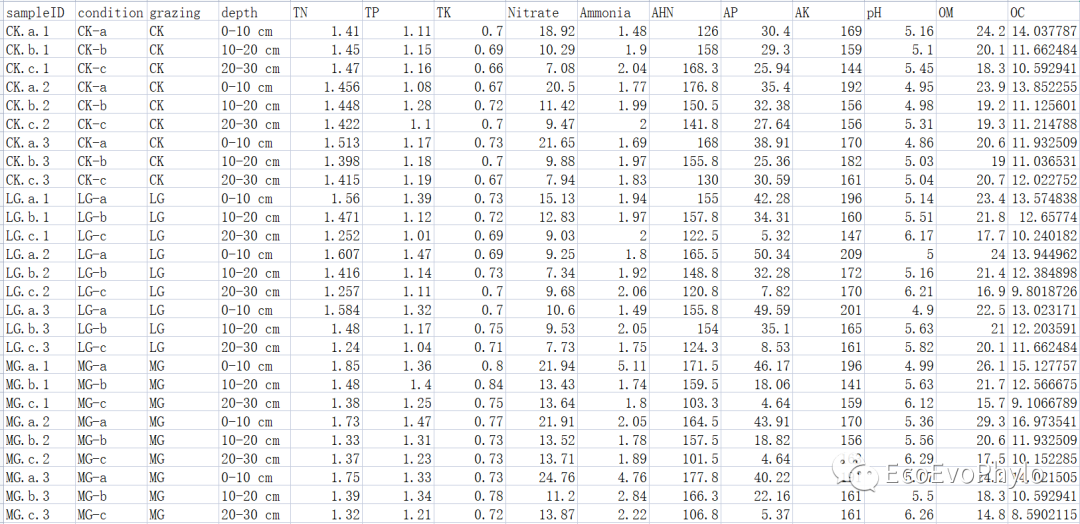
图2|环境因子及分组信息表，env.csv。行为样品名称，列为环境因子名称和分组信息，共有11个环境变量，3个分组信息。

1.2数据探索

library(rstatix)library(ggplot2)library(viridis)library(dplyr)library(tidyverse)# 1.2.1 分组数据描述统计##统计结果包括：中位数，均值，四分位数，中位数绝对偏差，标准差、标准误和置信区间等data %>%  group_by(condition) %>%  get_summary_stats()   

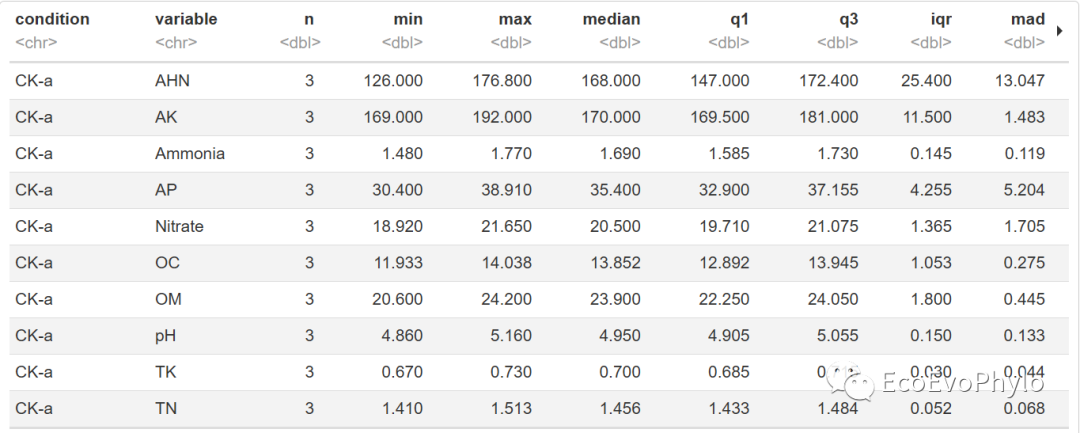
图3|数据描述统计。

# 1.2.2 数据分布可视化data[-c(1:3)] %>%  map(scale) %>% # 数据标准化  data.frame() %>%  gather(key = "features",value = "value") %>%  group_by(features) %>%  ggplot(aes(value,color=features))+  geom_density()+  theme_bw()

图4|数据分布可视化。

# 1.2.3 多元正态分布检验data %>%  select(names(data[-c(1:3)])) %>%   mshapiro_test() %>%  p.adjust() # p<0.05,数据不满足多元正态分布。可以换其他方法，也可以继续进行PCA分析。##    statistic      p.value ## 6.301624e-01 5.323599e-08

# 1.2.4 pearson相关性分析cor <- data %>%   select(names(data[-c(1:3)])) %>%  cor(.,method = "pearson")cor

图5|pearson相关性矩阵。

# 1.2.5 Bartlett's test of sphericity(球形检验)library(psych)cor %>%  cortest.bartlett(.,n=nrow(data)) # p<0.05变量间相关，可用于因子或主成分分析。## $chisq## [1] 508.746## ## $p.value## [1] 1.00108e-74## ## $df## [1] 55

# 1.2.6 Kaiser-Meyer-Olkin Measure of Sampling Adequacy(KMO采样充分性检验)cor %>%  psych::KMO() # 根据Kaiser提出的经验原则，变量适合性处于一般到良好。## Kaiser-Meyer-Olkin factor adequacy## Call: psych::KMO(r = .)## Overall MSA =  0.74## MSA for each item = ##      TN      TP      TK Nitrate Ammonia     AHN      AP      AK      pH      OM ##    0.72    0.76    0.62    0.76    0.57    0.86    0.70    0.89    0.84    0.71 ##      OC ##    0.71

二、探索性因子分析(EFA)

探索性因子分析与主成分分析的主要目标都是降低原始数据的维度，但探索性因子分析是有模型假设的，通常会假设原始变量及其相关性的潜在维度或结构。因子分析的模型有很多，常用的是公共因子模型(common factor analysis model),假设多个原始变量间有共有方差+误差项，某一原始变量等于潜变量的线性方程+误差项，提取的因子代表某些原始变量的相关关系，最终的目的是为了尽可能重现原始变量的相关性或协方差矩阵。

因子分析需要有相关性矩阵，矩阵中对角线的元素会根据因子提取方法(ML除外)而发生变化。因子提取的方法很多，PCA是其中之一，与其它因子提取方法的不同之处，主要是原始矩阵中对角线的值不一样，因此下面统一称为因子分析。

探索性因子分析中的因子载荷不是唯一的，将根据选择从程序中提取的因素数量而变化。但PCA中，无论提取2个或更多因子，都不会改变与提取的这些因子相关的载荷或权重。

2.1 确定提取因子(潜变量)数量

因子分析分析过程中有很多步骤需要人的决策，所以结果因输入、模型假设和其他关键决策而有差异。因子载荷给定变量的效果通常取决于因子分析中提取的因子数量，所以进行因子分析前确定提取因子轴的数量很重要，在分析结果描述中也必须注明提取了多少因子。

因此在开始因子分析时，使用PCA计算特征值，可以为因子分析提供良好的提前检查。

根据因子分析的特征值或碎石图确定最佳潜变量数量，选择的因子最好能代表数据方差的70%以上,一般来说，PCA保留的因子的特征值最好都大于1，其它因子提取方法保留的因子的特征值最好都大于相关性矩阵对角线值的均值。

# 2.1.1 因子分析确定提取因子数量-PCA法## 使用principal()进行PCA分析，输入数据可以是原始数据矩阵或者相关性系数矩阵。#page(principal) #查看函数代码library(psych)pca2 <- principal(data[-c(1:3,12)], #降维数据不包括pH,后续将会以pH为因变量进行回归分析。                 #r = cor, #也可使用变量相关性矩阵，但是样本得分需要自己计算。                 cor="cor",                 scores = TRUE,                 residuals = TRUE, # 输出结果中包含残差。                 nfactors = 10,# nfactors设置主成分数目                 rotate="none", # 不设置因子旋转方法                 ) pca2$Vaccounted # 某个因子的特征值等于因子载荷平方和。
## 绘制碎石图-确定最佳因子数量plot(pca2$values,type = "b",ylab = "Eigenvalues",xlab = "Component")text(pca2$values,labels = round(pca2$values/ncol(data[-c(1:3,12)])*100,2))abline(a=1,b=0,col="red",lty=2)

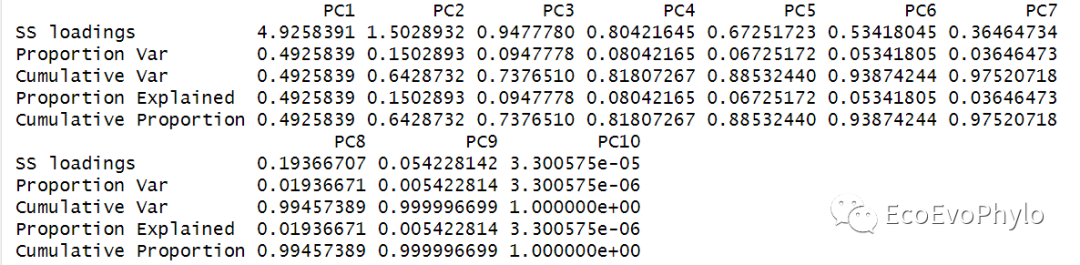
图6|PCA法提取因子。PC1-PC3累积解释变量方差>70%。

图7|PCA法提取因子碎石图。由碎石图可以看出，第一个因子以相对较大的特征值占主导地位，而其他因子的特征值的大小则逐渐减弱。前3个因子即可代表超过70%的数据方差，但是PC3的特征值

fa()中提供了六种算法估计载荷和公共因子(估计特定变量与数据矩阵中其它变量有多少共同方差)等参数：minimum residual (minres, aka ols, uls), principal axes, alpha factoring, weighted least squares, minimum rank和maximum likelihood。principal()使用PCA法提取因子。factanal 则是使用ML法提取因子。除PCA以外，其它因子提取方法都假设某一原始变量等于潜变量的线性方程+误差项。PCA提取方法则没有误差项，它认为原始变量的方差都可以由因子(潜变量)解释，其使用的相关性矩阵的对角线值为1。

# 2.1.2 因子分析确定提取因子数量-迭代主轴因子法(IPA)## 使用fa()进行因子分析。library(psych)fa0  <- psych::fa(        data[-c(1:3,12)],        cor ="cor", # 计算相关性矩阵的方法，cor表示Pearson。        scores = TRUE,        residuals = TRUE, # 输出结果中包含残差。        nfactors = 5,# nfactors设置提取因子数目。最后几个因子轴特征值<0.1，所以设置了一个稍小的数值。        rotate="none", # 不设置因子旋转方法        min.err = 0, # 设置迭代过程中，公因子方差变化不大于0，迭代才停止。        n.iter=99, # bootstrap分析重复次数,计算因子载荷置信区间。        SMC = TRUE,#默认设置squared multiple correlations为初始矩阵对角线公因子方差。设置为FALSE，可设置初始矩阵对角线为1。        fm = "pa", # PA法分析的是协方差，相关性矩阵的对角线值是公因子方差估计值，即变量能被潜变量代表的方差。        max.iter = 120 # 结果收敛的最大迭代次数，重复进行主轴因子法(PA)提取因子。                 ) fa0$Vaccounted
## 相关性矩阵对角线均值计算smc(data[-c(1:3,12)]) # 这是初始对角线值。fa0$communality # 这是最后确定的对角线值，即公因子方差。fa0$communality %>% mean # 因子特征值最好大于0.7623729,设置的提取因子数不同，此值会有变化。
## 绘制碎石图-确定最佳因子数量plot(fa0$values,type = "b",ylab = "Eigenvalues",xlab = "Component")text(fa0$values,adj=c(0.2,0.5),     labels = paste(round(fa0$values/ncol(data[-c(1:3,12)])*100,2),"%",sep = "")) # 这里百分比计算的分母，包含原始变量的误差项。abline(a=mean(fa0$communality),b=0,col="red",lty=2)

图8|IPA法提取因子。fa()进行PA提取因子时，将提取因子数目设置为原始变量数量，可能会报错：“Error in if (nitems[i] < 1) { : missing value where TRUE/FALSE needed”，设置为一个稍小于原始变量数量的值，可能会报错：”Error in l[id] : subscript out of bounds“。这是因为提取的因子的特征值必须大于0.1才行，这里解决方法就是先设置一个较小的值，然后查看fa0$values，再重新根据特征值设置提取因子数目。

图9|IPA法提取因子碎石图。由碎石图可以看出，最后几个因子轴特征值。结果显示可以选择top2因子轴。

平行分析是使用模拟数据估计与原始模型相同的因子模型，经过多次模型获得的特征值被平均化，然后与原始因子模型进行比较。如果原始因子模型的某个因子的特征值大于模拟数据特征值的均值，则该因子则应该保留。可以看出，跟直接进行因子分析确定的提取因子数量的情况差不多。这些都是确定因子数量的数学方法，实际因子数量的选择还是应该根据自己的数据情况和想要研究的问题来确定，后续因子旋转后也是一样，要看每个因子对原始数据的代表情况，如果有自己想要研究的变量，并没有被潜变量很好的代表，则应该考虑将该变量单独列出，其余变量重新做因子分析。因此，进行因子分析前的，原始变量间关系的探索也是很重要的，原始变量间具有相关关系，才能更好的查看数据具有的维度和对数据进行降维。

# 2.1.3 平行分析确定应提取的因子个数# ## 平行分析确定应提取的因子个数-psych包pa1 <- fa.parallel(  data[-c(1:3,12)],  fa = "fa", # "both"可选择同时进行PCA和因子分析。  fm = "pa",  n.iter=99,  nfactors = 5,  SMC = TRUE,  )
pa2 <- fa.parallel(  data[-c(1:3,12)],  fa = "pc", # 进行PCA。  n.iter=99,  nfactors = 5,  SMC = FALSE,  )

## nFactors包library(nFactors)ev <- eigen(cor(data[-c(1:3,12)],use = "na.or.complete")) # 获取特征值pa3 <- parallel(  subject=nrow(data),# subject指样本个数  var=ncol(data[-c(1:3,12)]),# var是指变量个数  rep=100,cent=.05) nS <- nScree(x=ev$values, aparallel=pa3$eigen$qevpea) # 确定探索性因子分析中应保留的因子。plotnScree(nS) # 绘制碎石图

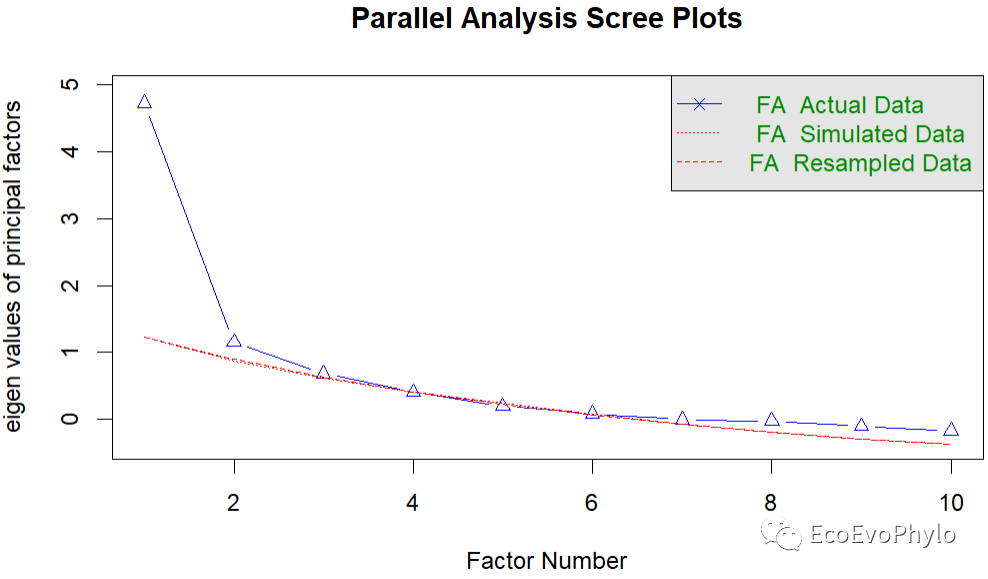
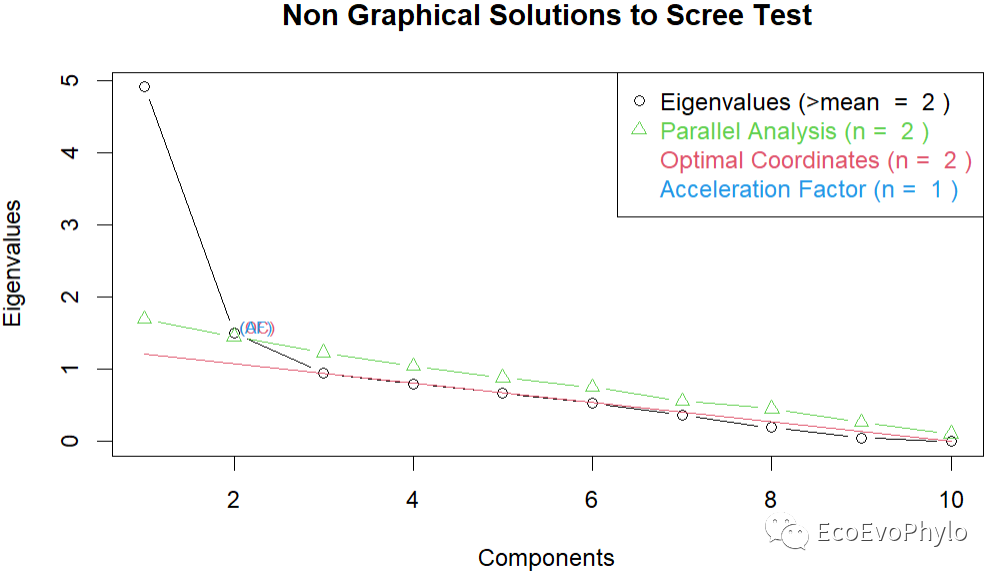
图10|平行分析碎石图。从上到下依次为PA、PCA法平行分析碎石图和nFactors包进行的因子提取平行分析。PCA和PA的平行分析结果显示适合提取2-3个因子轴。

最后决定提取2个因子轴，继续进行分析。因子分析最后得到的特征值总和如果大于相关性矩阵的对角线之和，则表明初始矩阵中对角线上的公因子方差估计有误，因此实际分析时，多常用迭代主轴因子法(IPA),重复多次PA提取因子过程，以计算得到的公因子方差(h2)更新初始矩阵的对角线公因子方差，直到PA提取的h2与初始矩阵更新后的对角线h2没有差异为止。

# 2.1.4 根据确定的提取因子数进行因子分析## IPA法提取两个因子轴library(psych)fa1  <- psych::fa(        data[-c(1:3,12)],        cor ="cor", # 计算相关性矩阵的方法，cor表示Pearson。        scores = TRUE,        residuals = TRUE, # 输出结果中包含残差。        nfactors = 2,        rotate="none", # 不设置因子旋转方法        min.err = 0, # 设置迭代过程中，公因子方差变化不大于0，迭代才停止。        n.iter=99, # bootstrap分析重复次数。        SMC = TRUE,#默认设置squared multiple correlations为初始矩阵对角线公因子方差。设置为FALSE，可设置初始矩阵对角线为1。        fm = "pa", # PA法分析的是协方差，相关性矩阵的对角线值是公因子方差估计值，即变量能被潜变量代表的方差。        max.iter = 120 # 结果收敛的最大迭代次数，重复进行主轴因子法(PA)提取因子。                 ) fa1

图11|未旋转IPA法因子载荷，fa1。结果输出中包含提取的因子载荷、变量公因子方差(h2)、唯一方差(u2)和com值。只要最后得到的因子是不相关的(未经过斜交旋转)，则因子载荷代表的意义都是原始变量与对应因子间的相关关系，即直接对应于双变量回归模型中的标准化系数，如表所示，TN在PA1的载荷0.95，可以解释为PA1每增加一个单位，TN就会平均增加0.95。即，scale(TN)=0.95*PA1+0.32*PA2+误差项。因子载荷的平方即代表因子对该原始变量的方差解释度，该原始变量在所有因子上的载荷的平方和，即为该变量的公因子方差(h2)。1-h2即为该变量未被所有因子代表的方差(唯一方差u2)。com的全称是“the complexity of the factor loadings for that variable”，表示Hoffman's index of complexity for each item,反应了一个变量在多大程度上反映了单一结构，如果变量仅在一个因子上有载荷，则等于1，如果在两个因子上均匀加载则为2。根据因子载荷绝对值大小，可以区分因子对原变量的代表性，很多文章建议以0.4(PCA法提取因子则推荐0.7)为阈值，来区分因子对原变量的代表性的显著性。同时在多个因子上的载荷都很高，也是需要注意的，会很难解释提取因子可能代表的意义。此时可以考虑更换提取因子的方法或进行因子旋转，最后再尝试删除变量。如果提取因子能很好的区分变量，有明显的代表意义，则可以进行后续分析。比如给因子命名，赋予其代表意义，计算样本得分以及进行信度检验。如果未经因子旋转的降维结果并不能很好的赋予因子轴以实际意义，后续可进行因子旋转。

## 输出结果-更多结果介绍请看后面### 特征值-因子(潜变量)捕获的原始数据的方差fa1$Vaccounted 
### 因子载荷=因子的特征向量*sqrt(特征值)print(fa1$loadings[1:ncol(data[-c(1:3,12)]),1:2],cutoff = 0)
### 变量公因子方差fa1$communality
### 公因子方差之和与特征值之和相等fa1$Vaccounted[1,] %>% sumfa1$communality %>% sum

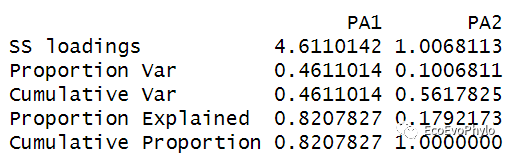
图12|未旋转特征值，fa1$Vaccounted。因子特征值与提取5个因子的特征值不同。

##  提取因子结果可视化-一般以0.4为载荷阈值### 因子载荷图fa.plot(fa1,labels = colnames(data[-c(1:3,12)]))
### 因子解示意图fa.diagram(fa1)

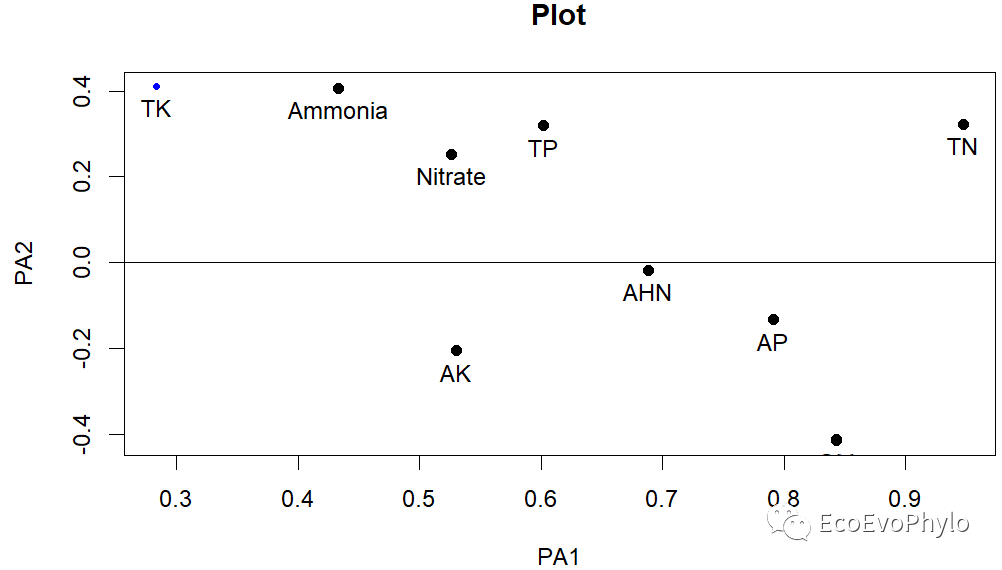
图13|IPA因子提取法未旋转因子载荷图。psych绘图函数将变量归类于载荷高的因子上。因子载荷是一个衡量原始变量与因子之间关系的参数。因子载荷的别称：PC loading, PC coefficient, weights和eigenvectors，当数据进行过标准化时，它们彼此没有区别。如图所示除TK以外的变量在因子1的载荷绝对值都>0.4,TK、Ammonia、OM和OC在因子2的载荷绝对值>0.4，但因为PA1已经加载了Ammonia、OM和OC，所以PA2只有TK。但是此结果于我们并没有什么理论意义，下面尝试进行因子旋转。

2.2 因子旋转

如果未经因子旋转的降维结果并不能很好的赋予因子轴以实际意义，后续可进行因子旋转。一般旋转后的因子解，每个因子轴的原始变量的载荷值会更接近或更远离0，即每个因子轴仅代表有限的几个原始变量组合的方差，有助于对每个因子轴的解释。经过旋转之后，每个变量的载荷发生改变，即对数据方差总量的贡献会改变，但是所有因子的方差解释度总和不会变。即，旋转前后因子分析选择的轴数量对方差总量的解释度不变。初始因子解产生的因子轴是正交变量，可以认为互相之间相关性为0，选择正交旋转(orthogonal rotation)法，旋转过后的因子轴间的相关性仍为0，若选择斜交旋转(oblique rotation：promax、oblimin、quartimin等)，经旋转的因子轴之间的相关性不为0。斜交旋转中，一个变量在一个因子上的载荷，是在控制了其他因素后估计的，因此得到的因子载荷相当于多重回归模型中偏标准化回归系数(偏相关关系)。执行正交还是倾斜旋转通常又取决于哪种解决方案的结果更容易解释，以及具有不相关或相关因子对研究人员是否更有实际或科学意义。

因子旋转的方法很多，比如principal()提供的有"varimax", "quartimax", "promax", "oblimin", "simplimax"和 "cluster"等方法。fa()中还有更多方法，?fa查看rotate参数选项，使用最多和书中介绍的是一种正交旋转法：varimax(极大方差法)，varimax使每个因子的平方载荷的方差最大化，从而使载荷或高或低，以更容易识别能代表特定变量的因子。varimax旋转过程中保持因子1和因子2的轴线的角度在90度，可以认为两个因子间的相关性为0。因子旋转前后的因子提取方法保持一致。

# 2.2.1 主轴因子法(PA)因子分析-极大方差旋转## 主轴因子法探索性因子分析library(psych)fa.var  <- fa(        data[-c(1:3,12)],        cor ="cor", # 计算相关性矩阵的方法，cor表示Pearson。        n.obs = 36,        scores = TRUE,        residuals = TRUE, # 输出结果中包含残差。        nfactors = 2,# nfactors设置提取因子数目        rotate="varimax", # 设置主成分旋转方法        min.err = 0, # 设置迭代过程中，公因子方差变化不大于0，迭代才停止。        n.iter=99, # bootstrap分析重复次数。        SMC = TRUE,#默认设置squared multiple correlations为初始矩阵对角线公因子方差。设置为FALSE，可设置初始矩阵对角线为1。        fm = "pa", # PA法分析的是协方差，相关性矩阵的对角线值是公因子方差估计值，即变量能被潜变量代表的方差。        max.iter = 120 # 结果收敛的最大迭代次数。                 ) fa.var
fa.var$Vaccounted # 2个潜变量共解释原始数据的~56.18%方差。

图14|IPA因子提取法极大方差旋转后的因子载荷。可以看出旋转前后，变量在每个因子上的载荷都发生了变化。

## principal()提取因子并进行因子旋转pca.var <- principal(  data[-c(1:3,12)],  residuals = TRUE, # 输出结果中包含残差。  nfactors = 2,# nfactors设置主成分数目  rotate="varimax", # 设置主成分旋转方法  use = "na.or.complete",)pca.var # 2个潜变量共解释原始数据的~65%方差。

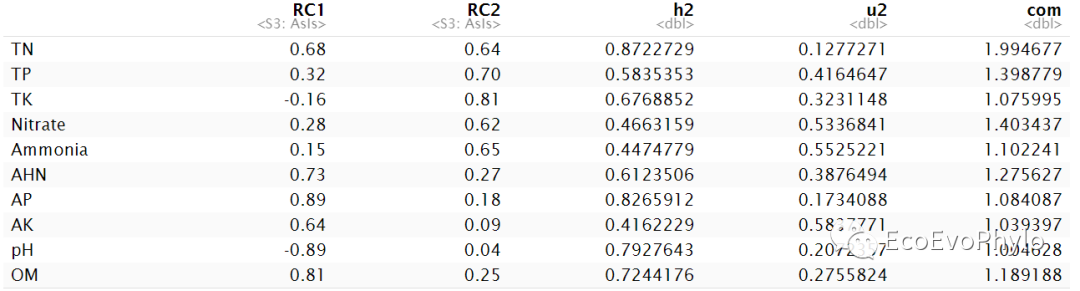
图15|PCA因子提取法极大方差旋转的因子载荷。与IPA法相比，PCA法的两个因子轴能解释的原始数据的方差比例高一些。在进行因子分析是，可以各种因子提取方法都尝试一下。

不同算法，因子分析的结果是有差别的,但是探索性因子分析，我们主要看因子(潜变量)对原始变量的协方差或相关性的代表情况，为下一步假设检验及回归建模做准备。当然，还是要看一下因子对每个变量的代表情况。

## 输出结果介绍### 特征值-因子(潜变量)捕获的原始数据的方差fa.var$Vaccounted 
### 因子载荷=因子的特征向量*sqrt(特征值)print(fa.var$loadings[1:ncol(data[-c(1:3,12)]),1:2],cutoff = 0)
### 变量公因子方差fa.var$communality
### Hoffman's index of complexity for each itemfa.var$complexity #反应了一个变量在多大程度上反映了单一结构，如果变量仅在一个因子上有载荷，则等于1，如果在两个因子上均匀加载则为2。
### 估计因子样本分数-默认“regression”法计算，因子变量载荷*样本中标准化变量值。# ?factor.scores # 查看更多估计因子得分的方法。# ?factor.stats # 查看因子分析更多统计结果解读。fa.var$scores
### 因子决定系数:推荐因子决定系数不小于0.9，估计因子样本分数才能作为原始变量的替代。fa.var$R2.scores

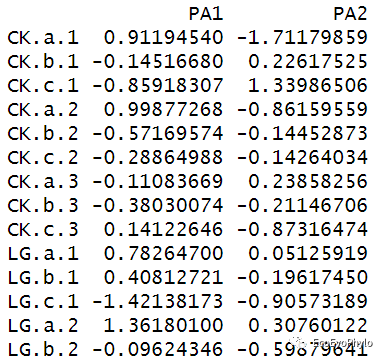
图16|IPA因子提取法极大方差旋转后的估计因子得分。

图17|IPA因子提取法极大方差旋转后的因子决定系数。推荐因子决定系数不小于0.9，估计因子样本分数才能作为原始变量的替代。

# 2.2.2 IPA法探索性因子分析结果可视化## 提取绘图数据### 估计因子样本分数-回归方法估计因子分数(fa.var.scores = data.frame(fa.var$scores)) %>% headwrite.csv(fa.var.scores,"fa.var.scores.csv",quote = FALSE)
### 特征值-潜变量捕获的原始数据的方差(fa.var.eig = data.frame(fa.var$Vaccounted)) # 2个潜变量共解释原始数据的~57.65%方差。write.csv(fa.var$Vaccounted,"fa.var.eig.csv",quote = FALSE)
### 因子载荷=因子的特征向量*sqrt(特征值)(fa.var.loadings <- print(fa.var$loadings[1:ncol(data[-c(1:3,12)]),1:2],cutoff = 0))write.csv(fa.var.loadings,"fa.var.loadings.csv",quote = FALSE)
## 原始环境因子数据结果绘图### 样本得分图(FA1 = round(fa.var.eig[2,1],4)*100)(FA2 = round(fa.var.eig[2,2],4)*100)
fa.var.scores %>%  mutate(grazing = factor(data$grazing,levels=c("CK","LG","MG","HG")),         depth = factor(data$depth,levels = unique(data$depth))) %>%  ggplot2::ggplot(    aes(PA1,PA2)) +   geom_point(        aes(        color = grazing,        fill = grazing,          alpha = depth), # 颜色透明度区分depth。        size=2.5)+  stat_ellipse(    level = 0.95,    linetype = 2,    aes(group = grazing,color = grazing))+    scale_color_manual(    values = ggsci::pal_d3("category10")(4) )+  scale_fill_manual(    values = ggsci::pal_d3("category10")(4) )+    labs(x=paste("Factor 1",FA1,"%"),y=paste("Factor 2",FA2,"%"))+  theme_bw()+  geom_hline(yintercept=0)+geom_vline(xintercept=0)+  theme(panel.grid=element_blank(),        legend.position="right",        axis.title = element_text(family = "serif", face = "bold", size = 18,colour = "black"),        axis.text = element_text(family = "serif", face = "bold", size = 16,color="black")) -> f1        ggsave("fa.var.factor.pdf", f1, device = "pdf")

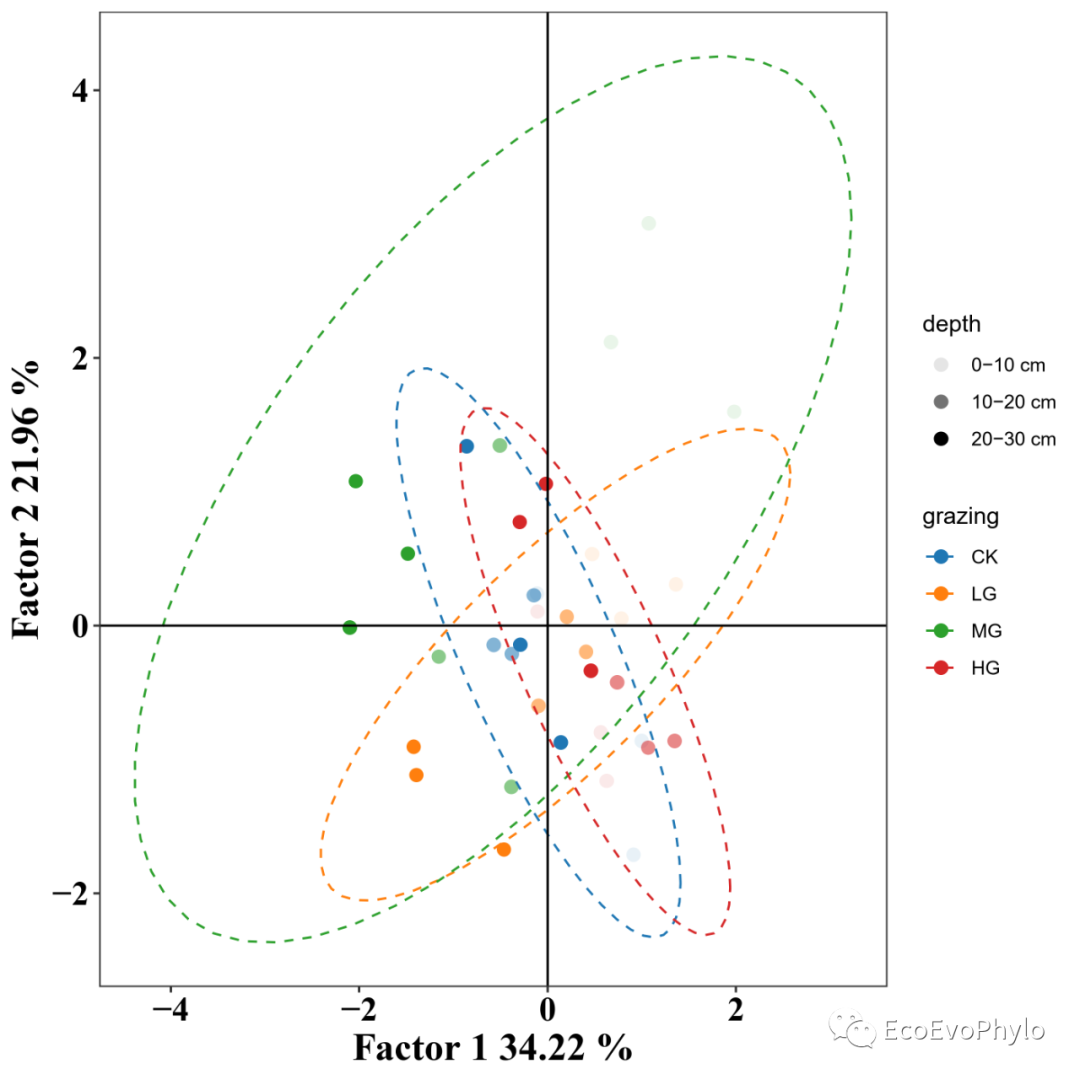
图18|IPA法极大方差旋转后的估计因子得分图。

### 因子对原始变量的方差解释图fa.var$communality # 变量公因子方差h^2，表示变量能被潜变量解释的方差。fa.var.loadings^2 %>% rowSums() # 所有变量的因子载荷平方和就是该变量的公因子方差。fa.var$uniquenesses # 唯一方差u^2,表示变量不能被新潜变量解释的方差。
#### 提取绘制潜变量对原始数据的方差的代表数据(fa.var.contrib = data.frame(  fa.var.loadings^2,  residuals=fa.var$uniquenesses) %>% as.matrix())fa.var.contrib[fa.var.contrib[,3] <0][3] <- 0 # 将负值改为0。write.csv(fa.var.contrib,"pca.var.contrib.csv",quote = FALSE)
#### 绘制新变量对原始数据的方差的代表性热图library(grDevices)library(corrplot)#hcl.pals() # 查看存在的颜色板名称col1 <- hcl.colors(10, "YlOrRd", rev = TRUE) #show_col(col1) # show_col()不能展示colorRampPalette()产生的颜色集pdf("fa.var.contrib.pdf",height = 8,width = 5,family="Times")corrplot(fa.var.contrib*100,         method = c("pie"),tl.col = "black",col = col1,         col.lim = c(0, 100), #设置bar颜色区间         is.corr=FALSE)dev.off()

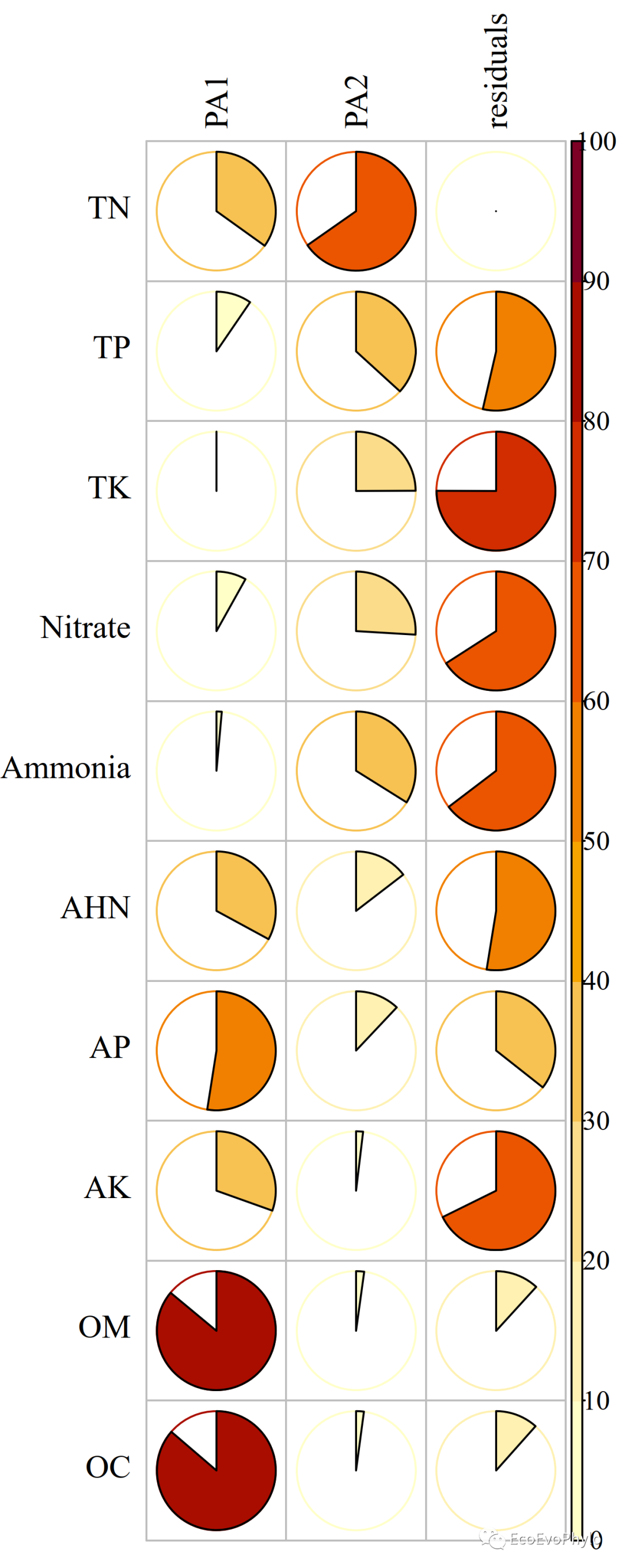
图19|IPA法极大方差旋转后的潜变量对原始变量的解释度。如图所示，因子1-2对Nitrate和AK等变量的代表性都小于50%。因此，因此降维后得到的潜变量不能很好的代表某些原始变量。此时，可以考虑：1）增加提取因子的数量，重新进行因子分析；或者2）可以考虑删除代表性不好的变量，重新进行降维，然后和删除的变量一起用于后续分析；3）或者将变量分成几个部分分别进行降维。

# 2.2.3 PCA法探索性因子分析结果可视化## 提取绘图数据### 估计因子样本分数-回归方法估计因子分数(pca.var.scores = data.frame(pca.var$scores)) %>% headwrite.csv(pca.var.scores,"pca.var.scores.csv",quote = FALSE)
### 特征值-潜变量捕获的原始数据的方差(pca.var.eig = data.frame(pca.var$Vaccounted)) # 2个潜变量共解释原始数据的~64.94%方差。write.csv(pca.var$Vaccounted,"pca.var.eig.csv",quote = FALSE)
### 因子载荷=因子的特征向量*sqrt(特征值)(pca.var.loadings <- print(pca.var$loadings[1:ncol(data[-c(1:3,12)]),1:2],cutoff = 0))write.csv(pca.var.loadings,"pca.var.loadings.csv",quote = FALSE)
## 结果绘图### 样本得分图(PC1 = round(pca.var.eig[2,1],4)*100)(PC2 = round(pca.var.eig[2,2],4)*100)
pca.var.scores %>%  mutate(grazing = factor(data$grazing,levels=c("CK","LG","MG","HG")),         depth = factor(data$depth,levels = unique(data$depth))) %>%  ggplot2::ggplot(    aes(RC1,RC2)) + # 提取的轴会按照特征值大小排序，与R1-R3并不是对应的。  geom_point(        aes(        color = grazing,        fill = grazing,          shape = depth), # 用性状区分depth。        size=2.5)+  stat_ellipse(    level = 0.95,    linetype = 2,    aes(group = grazing,color = grazing))+    scale_color_manual(    values = ggsci::pal_d3("category10")(4) )+  scale_fill_manual(    values = ggsci::pal_d3("category10")(4) )+  scale_shape_manual(    values = c(16,17,15))+    labs(x=paste("PC1",PC1,"%"),y=paste("PC2",PC2,"%"))+  theme_bw()+  geom_hline(yintercept=0)+geom_vline(xintercept=0)+  theme(panel.grid=element_blank(),        legend.position="right",        axis.title = element_text(family = "serif", face = "bold", size = 18,colour = "black"),        axis.text = element_text(family = "serif", face = "bold", size = 16,color="black")) -> f3        ggsave("pca.var.factor.pdf", f3, device = "pdf")
### 因子对原始变量的代表图pca.var$communality # 变量公因子方差h^2，表示变量能被潜变量解释的方差。pca.var.loadings^2 %>% rowSums() # 所有因子的因子载荷平方和就是该变量的公因子方差。pca.var$uniquenesses # 唯一方差u^2,表示变量不能被新潜变量解释的方差。pca.var.loadings <- print(pca.var$loadings,cutoff = 0)[1:ncol(data[-c(1:3,12)]),1:2]
#### 提取绘制新变量对原始数据的方差的代表数据(pca.var.contrib <- data.frame(  pca.var.loadings^2,  residuals=pca.var$uniquenesses) %>% as.matrix())write.csv(pca.var.contrib,"pca.var.contrib.csv",quote = FALSE)
#### 绘制新变量对原始数据的方差的代表性热图library(grDevices)library(corrplot)#hcl.pals() # 查看存在的颜色板名称col1 <- hcl.colors(10, "YlOrRd", rev = TRUE) #show_col(col1) # show_col()不能展示colorRampPalette()产生的颜色集pdf("pca.var.contrib.pdf",height = 8,width = 5,family="Times")corrplot(pca.var.contrib*100,         method = c("pie"),tl.col = "black",col = col1,         col.lim = c(0, 100), #设置bar颜色区间         is.corr=FALSE)dev.off()

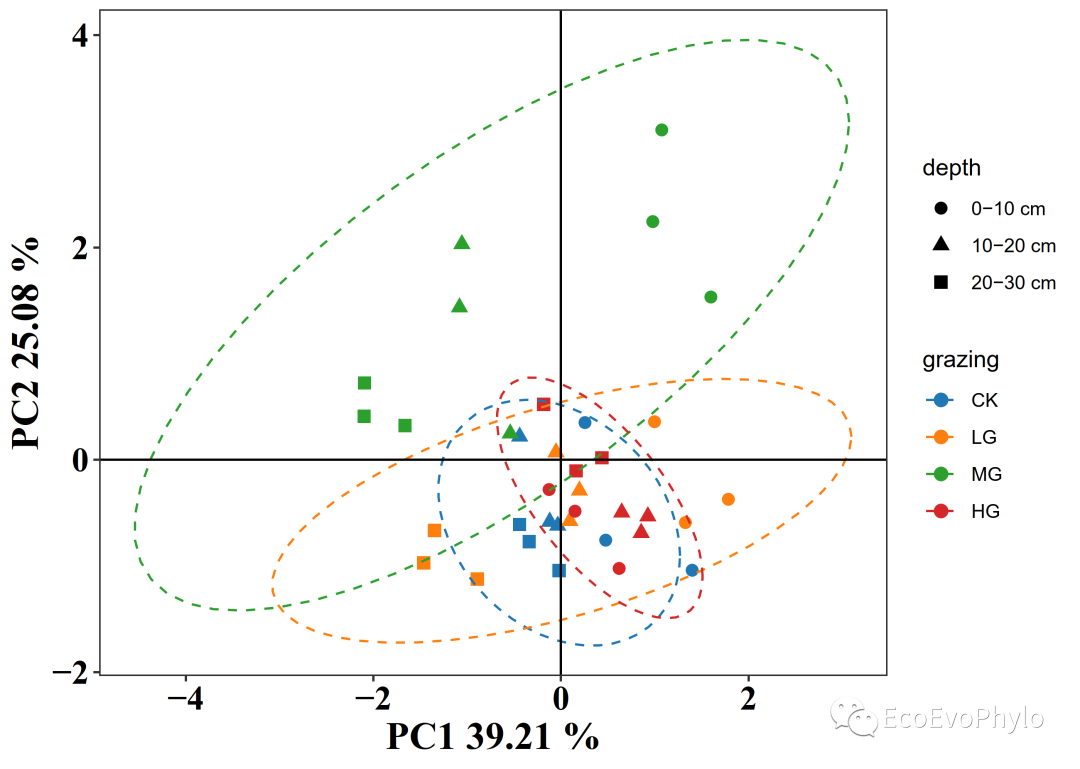
图20|PCA法极大方差旋转后的结果绘图。从上到下，依次为估计因子得分、潜变量对原始变量的解释度。IPA与PCA的分析结果有明显的差异。探索性因子分析主要就是为了对数据降维，寻找到原始变量的数据结构，不同方法之间的结果不同，不用担心，选用符合自己数据实际意义的分析结果就行。正如5.2.1输出结果介绍部分所说，估计因子得分能否用于代替原始变量进行后续分析，还需要看因子决定系数。

在得到符合研究实际意义的因子分析结果后，如果因子决定系数生成因子得分是通过对某一因子上载荷最强的变量进行加总或平均得到的未经加权的原始值。与估计因子得分一样，生成因子得分也需要进行信度(alpha)检验，范围为0-1，一般阈值为0.7。

# 2.2.4 生成的因子样本分数-通过对某一因子上载荷最强的变量进行加总或平均得到的未经加权的原始值。## 根据PCA法因子提取结果：将TN,AHN,AP,AK,OM,OC归为PC1，其余变量归为PC2。(itemlist <- list(  pc1 = c("TN","AHN","AP","AK","OM","OC" ),  pc2 = c("TP","TK","Nitrate","Ammonia")))
## 计算生成因子得分-通过对某一因子上载荷最强的变量进行平均得到的未经加权的原始值。scores <- score.items(itemlist,            data[-c(1:3,12)],            totals = FALSE) # totals=TRUE，则计算总和。scores$scores # 每个因子代表的变量的均值，随后就可根据实际意义，对因子进行命名。describe(scores$scores) # 生成因子得分描述统计。
## 检验因子得分的信度-1-误差方差的比例a1 <- psych::alpha(# 克朗巴哈系数alpha一般以0.7为阈值。  data[c(itemlist$pc1)],  check.keys=TRUE) # 反转具有负载荷因子的变量，默认为FALSE。a1$total$std.alpha #包含的变量数多于1，才有计算结果。a2 <- psych::alpha(  data[c(itemlist$pc2)],   check.keys=TRUE) # 克朗巴哈系数alpha一般以0.7为阈值。a2$total$std.alpha #包含的变量数多于1，才有计算结果。

图21|PCA法极大方差旋转后的生成因子得分。通过将因子方差解释度高的变量进行平均得到的。

图22|PCA法极大方差旋转后的生成因子得分的可靠性检验。结果显示，PC1的代表性很好，PC2稍微差一些。后面都采用生成因子得分进行后续分析。

## 生成因子得分可视化pdf("pca.scores.pdf",height = 3,width = 8,family = "Times")scores$scores %>%   data.frame() %>%  mutate(grazing = factor(data$grazing,levels=c("CK","LG","MG","HG")),         depth = factor(data$depth,levels = unique(data$depth))) %>%  gather(key = "PC",value = "value",-grazing,-depth) %>%  ggplot(aes(x=PC,y=value))+  geom_vline(xintercept=0,color = "grey50") +  geom_point(aes(color = grazing,shape=depth))+  scale_color_manual(    values = ggsci::pal_d3("category10")(4) )+  facet_wrap(~PC,nrow = 2,scales = "free") +    scale_x_discrete(expand = c(0,0))+  scale_y_continuous(expand = c(0,0))+  coord_flip() +  labs(x=NULL,y="scores")+  theme_minimal()+  theme(    panel.background = element_blank(),    panel.grid=element_blank(),    axis.ticks = element_line(),    axis.line.x = element_line(),    strip.text =element_blank()      )dev.off()

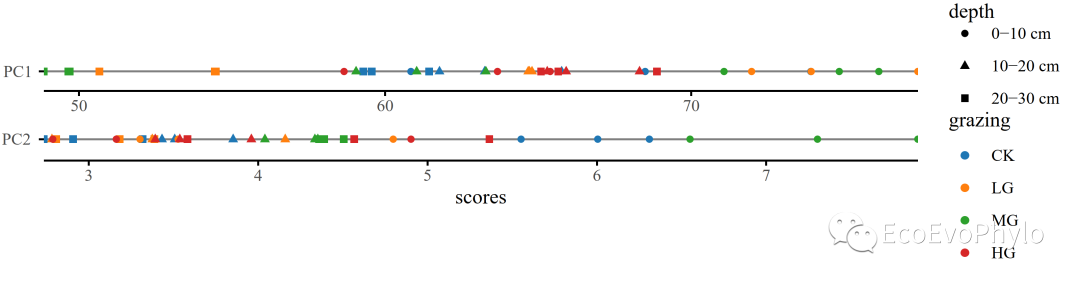
图23|PCA法极大方差旋转后的生成因子得分绘图。单轴绘图，查看单个因子轴对样本的区分能不能很好的契合分组信息。

2.3线性回归分析

# 2.3.1 使用估计因子得分进行线性回归分析## IPA法极大方差旋转后估计因子得分与pH回归(falm = lm(pH ~ .,data=bind_cols(fa.var.scores,data[12]))) %>% summaryfalm %>% summary

## PCA法极大方差旋转后估计因子得分与pH回归(pclm = lm(pH ~ .,data=bind_cols(pca.var.scores,data[12])))pclm %>% summary
# 2.3.2 绘制系数效应图library(sjPlot)## IPA法极大方差旋转后估计因子得分与pH回归plot_model(falm,           sort.est = TRUE,#按系数值大小排序。           show.values = TRUE, # 显示系数值和显著性标签。           value.offset = .3)

## PCA法极大方差旋转后估计因子得分与pH回归plot_model(pclm,           sort.est = TRUE,#按系数值大小排序。           show.values = TRUE, # 显示系数值和显著性标签。           value.offset = .3)           

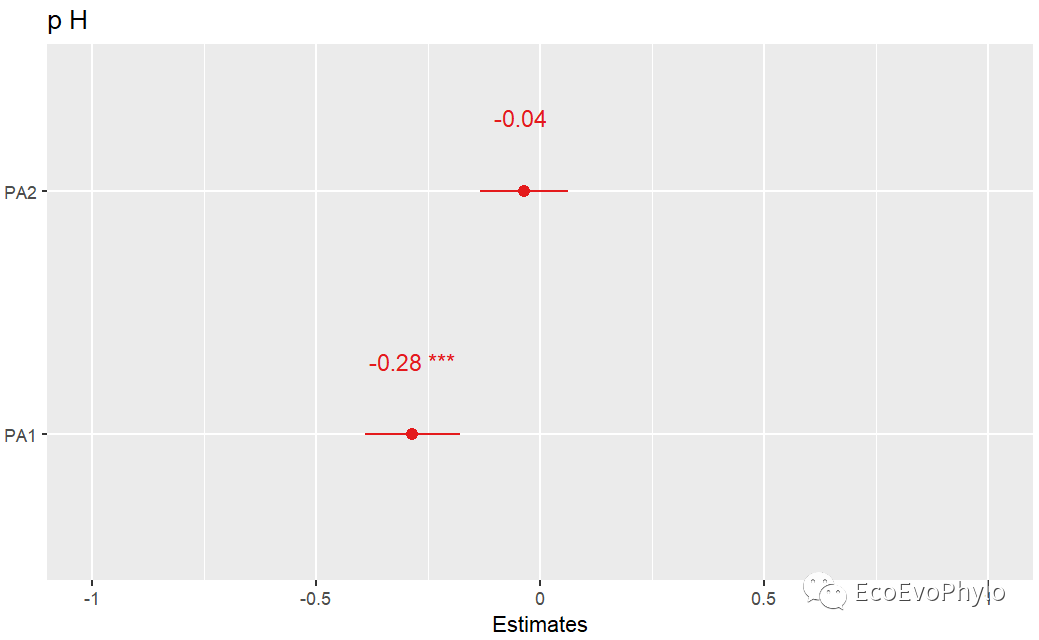
图23|线性回归效应图。从上到下依次为：IPA法、PCA法极大方差旋转后估计因子得分与pH回归的系数效应图。

两种方法得到的估计因子得分与pH的拟合结果都是显著的。Adjusted R-squared分别为0.4543和0.6033，但是PA2与RC2的回归系数绝对值都很小，且都小于标准误差，说明回归效果一般。因子分析是否“成功”的主要标准通常是看因子解是否具有实质性意义。如果研究人员能够在因子解中观察到一个合理的因子解方案，那么探索性因子分析通常被认为是成功的。另一方面，如果因子解在实质性或科学层面上没有什么意义，那么探索性因子分析通常被认为是失败的。所以进行探索性因子分析前，最好有足够的理论知识，提前将原始变量分类，再分别进行降维也可。