研究场景

因子分析(探索性因子分析)用于探索分析项(定量数据)应该分成几个因子(变量),比如20个量表题项应该分成几个方面较为合适;用户可自行设置因子个数,如果不设置,系统会以特征根值大于1作为判定标准设定因子个数。

数据格式

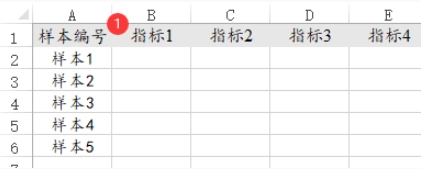
因子分析时，一列标识1个指标，一行为1个样本；如果为面板数据，比如100家公司每家公司10年，那么就会有100*10=1000个样本，可能需要单独两列分别是公司名和年份来标识面板格式而已，但因子分析并不区分是否面板数据，只针对指标进行分析即可，另一般分析样本量需要超出分析项（指标）的5倍，类似数据格式如下图：

SPSSAU操作

1.上传数据

登录账号后进入SPSSAU页面，点击右上角“上传数据”，将处理好的数据进行“点击上传文件”上传即可。

2.拖拽分析项

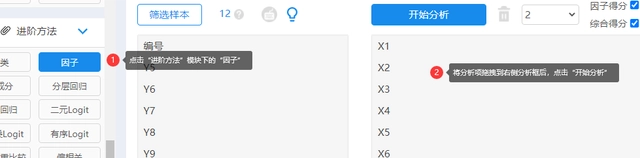
在“进阶方法”模块中选择“因子”方法，将分析项定量拖拽到右侧分析框内，点击“开始分析”即可。

补充说明：如果有预期想提取的因子个数，可以主动设置输出的因子个数勾选“因子得分”与“综合得分”会在左侧分析框生成新的变量，标题如CompScore*****（综合得分）、FactorScore*****（因子得分）。因子得分可用于进一步分析，比如聚类分析，回归分析使用等；综合得分可用于对比排名等。

因子个数：多数情况下，我们在分析时已经带着主观预期，希望题项如何归类，此时可以直接设置对应的因子个数。

调整分析项

当前有一份数据,共涉及A1~A4,B1~B4,C1~C3,D1~D3共14个量表题，希望将此14个量表题使用因子分析浓缩成几个维度。从背景情况上看，预期此14个题目可分为4个维度，分别称作A，B，C和D维度。当然有可能个别项并不合适，因此有可能对其进行删除处理。

1.第一次分析

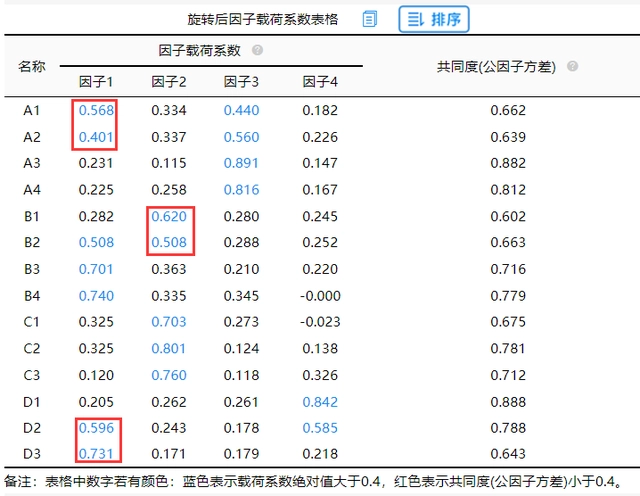
从上图中可以看出：

A1~A4这4项，它们全部对应着因子3时，因子载荷系数值均高于0.4，说明此4项应该同属于一个维度，即逻辑上A1~A4这4项，并没有出现‘张冠李戴’现象。但是A1和A2这两项出现‘纠缠不清’现象，A1和A2除了可以对应因子3，也可以放在因子1下面。一般出现‘纠缠不清’现象时，暂时保留，先处理清楚‘张冠李戴’问题更好。

B1~B4共4项，B2,B3,B4这3项对应着因子1下面，但是B1却对应着因子2，因此B1这项属于‘张冠李戴’，应该将B1删除。B2同时对应因子1和因子2均可，属于‘纠缠不清’，暂不处理B2。

C1~C3共3项，此3项均对应着因子2，此3项并没有出现‘纠缠不清’或者‘张冠李戴’问题。

D1~D3共3项，D3出现了‘张冠李戴’问题，应该进行删除处理。D2出现了‘纠缠不清问题’（可对应因子1和因子4），应该给予关注。

总结上述分析可知：B1和D3这两项出现‘张冠李戴’，应该首先将此两项删除；而A1，A2，B2，D2共四项有出现‘纠缠不清现象’，暂时不处理（进行关注即可）。将B1和D3这两项删除后，进行第二次分析。

2.第二次分析

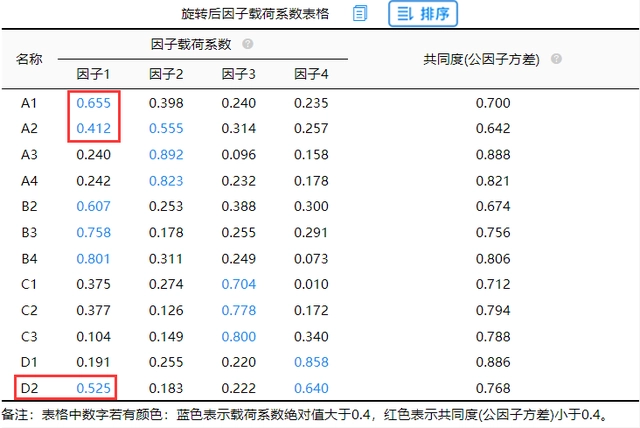
总结可知：A1出现“张冠李戴”现象，应该将A1先删除后再次进行第3次分析，另对A2和D2（“纠缠不清”）这两项给予关注。

3.第三次分析

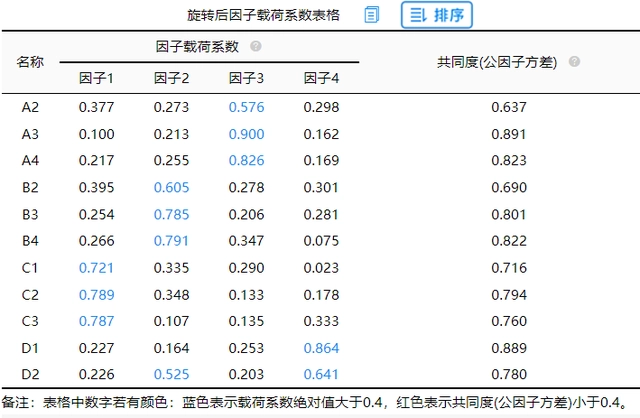
D2可同时出现在因子2和因子4下面，但考虑到D维度当前仅余下2项，因而表示可以接受，最终是将D2归纳到因子4即D维度下面。最终找出A，B，C和D共4个维度，它们分别与项之间的对应关系良好。因子分析结束。“纠缠不清”：比如A1可归属为A维度，同时也可归属到C维度，这种情况较为正常（称作‘纠缠不清’），需要结合实际情况处理即可，可将A1删除，也可不删除，带有一定主观性。因子分析是一个多次重复的过程，比如删除某个或多个题项后，则需要重新再次分析进行对比选择等。最终目的在于：维度与分析项对应关系，与专业知识情况基本吻合。

“张冠李戴”：比如A1归属为A维度，但是却归属为C维度下，出现这种情况一般进行删除，重新分析。

SPSSAU分析

1.KMO 和 Bartlett 的检验

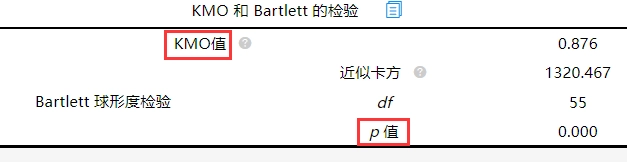
使用因子分析进行信息浓缩研究，首先分析研究数据是否适合进行因子分析，从上表可以看出：KMO为0.876，大于0.6，满足因子分析的前提要求，意味着数据可用于因子分析研究。以及数据通过Bartlett 球形度检验(p

2.方差解释率表格

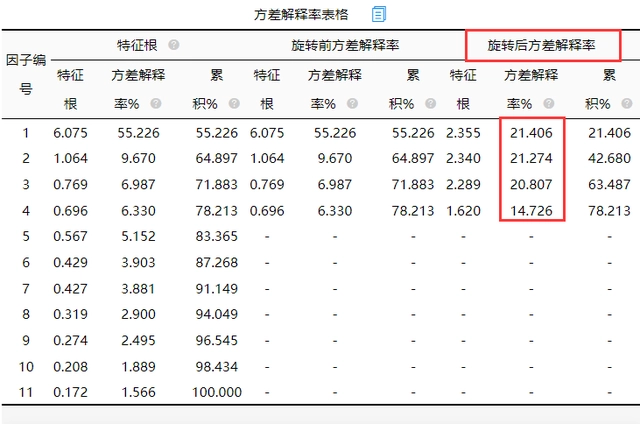
主要用于判断提取多少个因子合适。以及每个因子的方差解释率和累计方差解释率情况。方差解释率越大说明因子包含原数据信息的越多。因子分析中，主要关注旋转后的数据部分。

从上表可知：累积方差解释率值为78.213%，说明提取出来的4个因子可以提取出总共11项中78.213%的信息量，而且四个因子的方差解释率（信息提取量）分别为：21.407%，21.277%，20.807%和14.723%。信息提取量分布较为均匀，综合说明本次因子分析结果良好。

补充说明：如果研究人员并没有预设维度。而选择默认选项，SPSSAU默认以特征根大于1作为标准。当然因子分析通常需要综合自己的专业知识综合判断，即使是特征根值小于1，也一样可以提取因子。

3.旋转后因子载荷系数表格

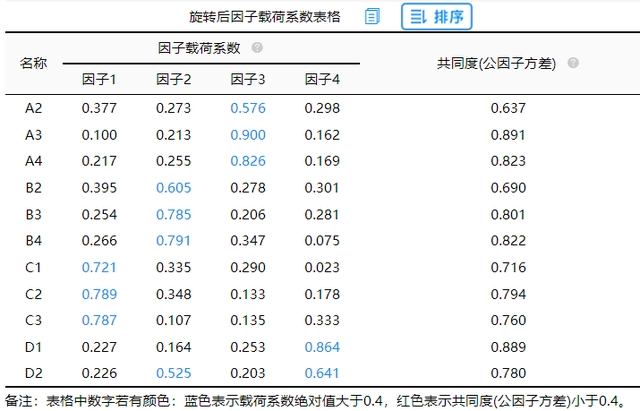
从上表可知：所有研究项对应的共同度值均高于0.4，意味着研究项和因子之间有着较强的关联性，因子可以有效的提取出信息。最终对浓缩出来的四个因子进行分别命名为：A，B，C和D维度。

4.碎石图

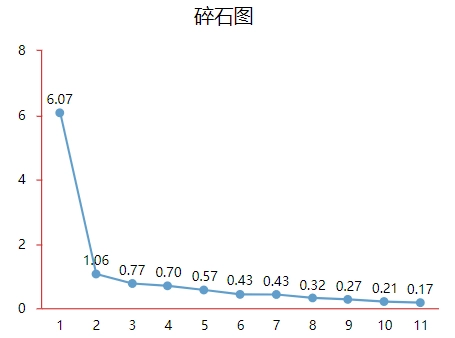
同时可结合碎石图辅助判断因子提取个数。当折线由陡峭突然变得平稳时，陡峭到平稳对应的因子个数即为参考提取因子个数。实际研究中更多以专业知识，结合因子与研究项对应关系情况，综合权衡判断得出因子个数。

补充说明：因子计算权重

5.成份得分系数矩阵

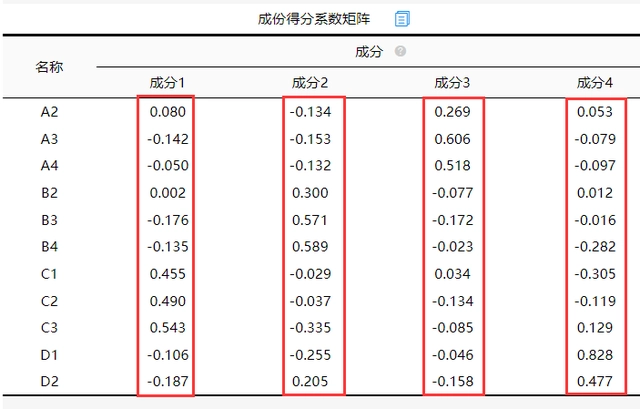
6.载荷图

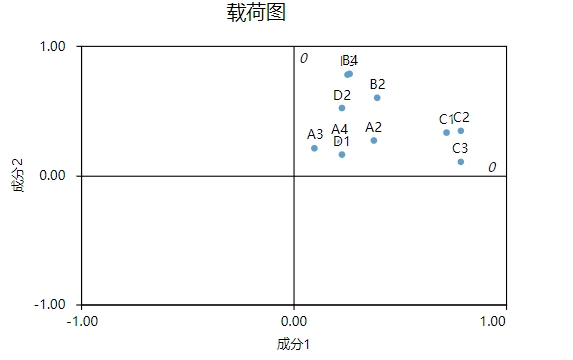
载荷图用于展示各因子与载荷值关系情况，建议结合实际情况使用即可。

第一：如果提取1个成分（或因子）时，则无法展示载荷成分图；

第二：如果超过个成分（或因子）时，可自主切换查看对应的载荷图。

其中X轴Y轴可以更改如下：

7.线性组合系数及权重结果

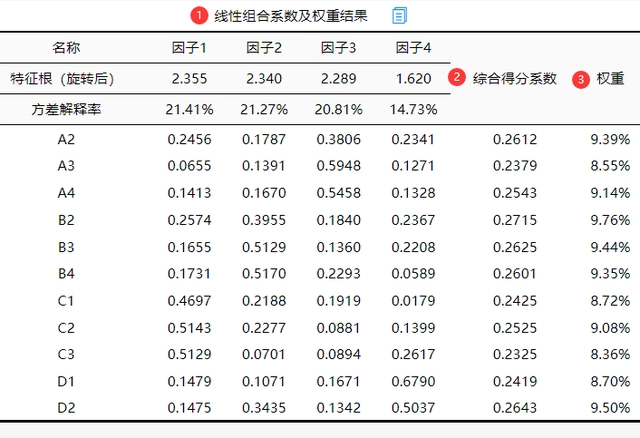
其它问题

1.因子分析计算权重？

如果使用因子分析的目的在于计算权重，此时可使用旋转后方差解释率值进行权重计算。比如提取2个因子，旋转后的方差解释率分别是39.759%,24.061%，旋转后累积方差解释率为63.820%。那么归一化（即除累积方差解释率）即得到权重，计算如下表：

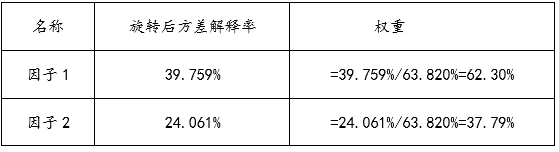
2. 无论如何均‘张冠李戴’或‘纠缠不清’？

‘张冠李戴’是需要处理的，如果无论如何都有‘张冠李戴’现象，意味着维度和题项间对应关系有问题。可考虑减少因子个数进行对比分析。

【特别提示：因子分析是一个来回多次重复对比，结合软件输出和自身专业知识情况综合选择对比找出最优结果的过程】‘纠缠不清’这种现象，多数时候并不需要处理。

3. 最大方差旋转问题？

SPSSAU默认使用最大方差旋转法（Varimax）对数据进行旋转。特征根，方差解释率和累积方差解释率这三项均区分旋转前和旋转后；如果让软件自动识别因子个数，是以旋转前特征根大于1作为标准；其余情况下的分析建议以旋转后作为标准。

4.综合得分如何使用？

综合得分可用于对比综合竞争力情况，综合得分值越高，此时综合竞争力越强。此类应用常见于经济、管理类研究，比如上市公司的竞争实力对比。

综合得分需要选中按钮才会生效，且SPSSAU单独生成一列新标题名称类似为：“Comp_score****”,一般情况下用户需要把综合得分的原始数据下载出来使用，通过右上角‘我的数据->下载’，可将综合得分下载出来使用。

5.‘分析之前是否需要对数据进行标准化处理’？

SPSSAU默认就已经进行过标准化处理，因此不需要再对数据处理。当然标准化后的数据再次标准化依旧还是自身没有任何变化，结果永远均一致。

6. 综合得分如何计算得到的？

SPSSAU默认提供保存综合得分，至于其计算原理，比如说提取得到4个因子，并且此4个因子的旋转后方差解释率分别是21.407%，21.277%，20.807%和14.723%；累积方差解释率值为78.213%。综合得分计算公式为：求和(因子得分*旋转后方差解释率)/累积方差解释率。如下图所示：

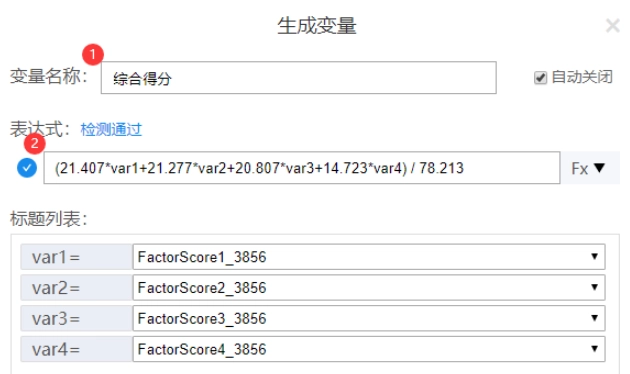
总结

因子分析往往是预处理步骤，后续还需要结合具体研究目的进行分析，如回归分析、聚类分析等。对于探索性因子分析完成指标权重，计算在实际研究中，通常会结合其他分析方法，比如主观赋权法（AHP层次分析法），或者客观赋权法（熵值法）进行权重计算，亦或是在主观赋权法和客观赋权法基础上，结合组合赋值法完成最终权重计算。