在数学中，某个概念、公式、定理的发现很难归功于一个时期、一个人，如，“平面”的概念从古希腊时期的朴素认识到20世纪的描述性定义跨度两千多年，“勾股定理”早在公元前2000年的古巴比伦已有记录，但第一个证明要直到公元前7世纪由毕达哥拉斯给出。同样，“余弦定理”的最终成型也经历了上千年。

欧几里得Euclid是古希腊著名的数学家，《几何原本》一书的作者，被誉为“几何学之父”；著名物理学家杨振宁“千古寸心事，欧高黎嘉陈”一诗中的“欧”指的就是欧几里得。Euclid在《几何原本》中对定理等的安排，由浅到深，从简至繁，全书主要以几何的形式呈现，也不乏有代数、数论等知识。

在《几何原本》第二卷的命题12和13中，我们能看到“余弦定理”的雏形。

命题12：在钝角三角形中，钝角所对的边上的正方形比夹钝角的二边上的正方形的和还大一个矩形的二倍.即由一锐角向对边的延长线作垂线，垂足到钝角之间一段与另一边所构成的矩形.【证明见附录1】

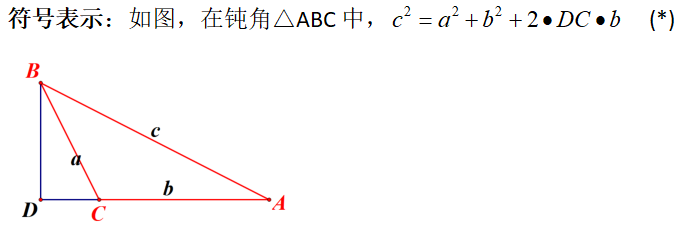
显然，《几何原本》中的这个定理是一个几何学定理，与三角学关系不大，但是请注意，命题中

,将其带入（*）易得：

不错，这就是三角学中著名的“余弦定理”。

尽管现在的我们看这些推理是简单的，但是欧几里得并没有跨出这重要的一步，另外一点也可以佐证——作为“余弦定理”重要特例的“勾股定理”、欧几里得将其放在了第一卷的最后，而锐角三角形下的“余弦定理”则放在了命题13。这样一个定理被拆分成了三个——锐角的、直角的和钝角的。这样不统一的、几何形式下“余弦定理”，需要直到15世纪才由另一位著名数学家从“三角学”的角度重新认识、并统一。

在法国，直至今日“余弦定理”仍然被叫做“卡西定理”（Theorem of Al-Kashi)，这是为了纪念给出真正意义上的“余弦定理”的阿拉伯数学家al-Kāshī。

al-Kāsh是中世纪晚期阿拉伯著名的数学家，在兀鲁伯创建的撒马尔罕天文台主持工作，并协助兀鲁伯编制了著名的《兀鲁伯星表》。

al-Kāsh的一个成就值得我们关注，这就是他在《圆周论》中从正方形出发将圆周率π精确到了小数点后16位，打破了祖冲之保持了近千年的世界纪录。

al-Kāsh还有另外两部著作：《弦与正弦之书》（The Treatise of Chord and Sine）和《算术之钥》（The Key to Arithmetic），前者第一次记录了正弦的三倍角公式：

而后者第一次给了“余弦定理”现在形式的描述。

利用三角学的一些知识，卡西将欧几里得《几何原本》中对“勾股定理”的证明图推广到了一般情形——余弦定理。

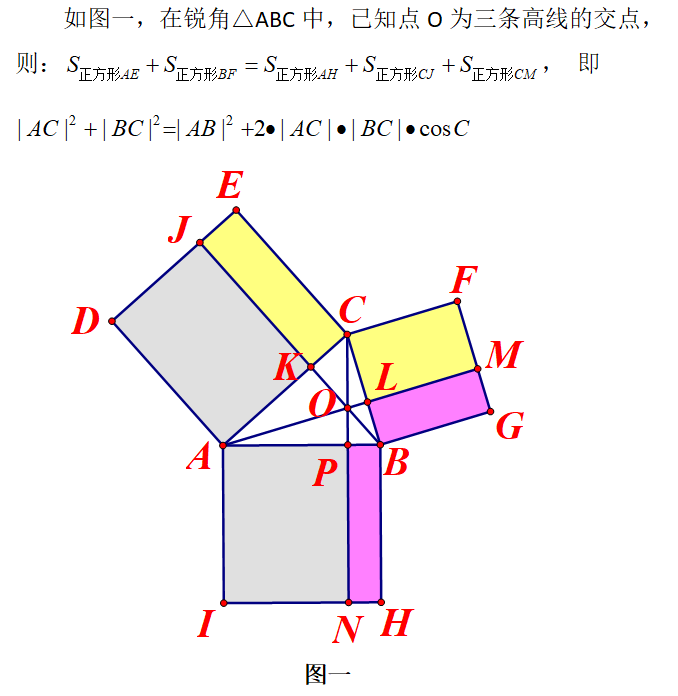
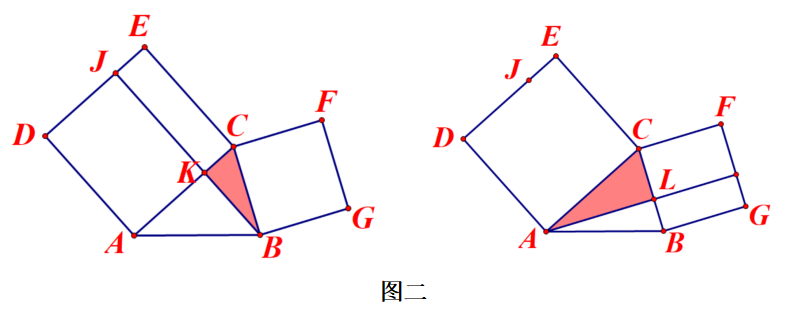
钝角的推理类似可得。

我们注意到，卡西在这里明确的用到了“余弦”这一概念，不是从纯几何，而是用到了“三角学”的相关知识。尽管没有使用符号，但卡西给了易于翻译成现代符号的“余弦定理”，并且将范围扩大到一般的三角形，即锐角、钝角、直角三角形均适用。

15世纪卡西的工作应该被16世纪的著名数学家韦达所熟知，韦达为余弦定理的推广起了促进作用。而且随着三角学成为日显重要的一门数学学科，“余弦定理”的用途也逐步凸显。

数学家们找寻了更多的方法来证明它，最成功的应该是使用向量的数量积：

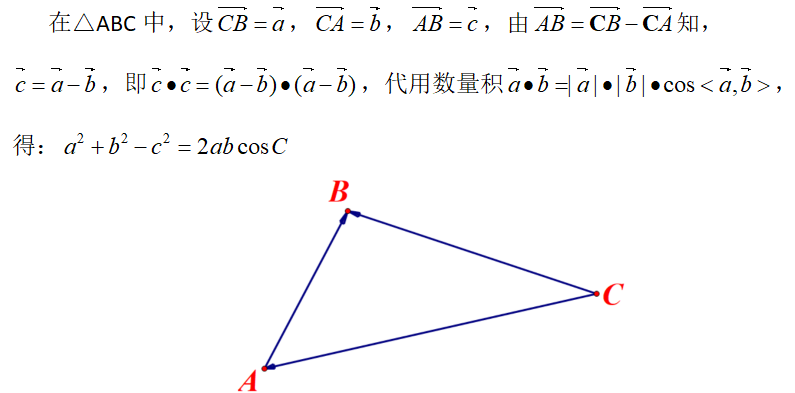
这个证明很简洁，而且对于任意三角形都适用、不需要分类处理，同时，该方法还很好的连接了三角与代数。因此，人教版高中数学教材（必修5）也将其录入其中。

总的来说，"余弦定理"最早以几何形式出现在欧几里得的《几何原本》中，后经阿拉伯数学家卡西的整理将其纳入“三角学”范畴，并经韦达的著作强力推广，但是仍然以文字或原始符号形式出现，现在高中课本中呈现的形式大约出现在19世纪左右。

附录一：命题12及其证明

附录二：命题13及其证明