贲友林工作室·发现||圆周率到底是怎么算出来的？

原创杨莉

贲友林学为中心

gh_d65a77ad0f0e

交流学为中心课堂探索的经历与思考。

【问题】

学习圆周率时，教材中的安排：用滚动法或绳绕法先测量大小不同的圆周长和直径，再算出周长除以直径的商，引出圆周率的定义。学生在真实操作过程中却发现，每一次的实验数据都不一样，有时误差还会很大，得数保留两位小数几乎得不到3.14。

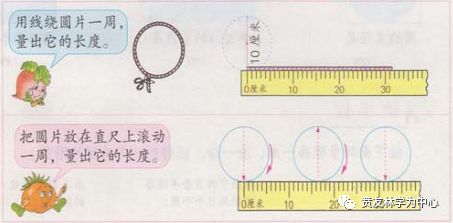
第一课时中刚利用“圆周长÷直径”求得圆周率，紧接着“试一试”就利用：“圆周率×直径”来计算圆周长，到底是“先有鸡还是先有蛋”？尽管学生相信了课本，相信了老师，但不免心存疑惑：圆周率到底是怎么算出来的？

【分析】

圆的周长和直径的比称为圆周率，我们可以通过测量来试着寻找圆周率。准备一个一次性纸杯和刻度尺，用刻度尺测量纸杯杯口的周长，会发现测量的结果大约为21cm,直径大约为7cm,而21÷7=3，所以可以说圆周率的近似值为3。

如果换成更大的纸杯来测量周长和直径，会得到π为3.1左右的数值，但却始终无法得到数学教材中π的近似值3.14。细看世界各国对圆周率的研究历史，不难发现，π是通过“计算”求出来的。

1、历史追溯

人们应该是在研究圆时，发现了π这个常数，然后继续利用圆来研究它。

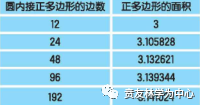
阿基米德（前287-212）发现，可以用圆的内接正多边形和外切正多边形计算π，因为一个圆的周长，总是大于其内接正多边形的周长，并小于其外切正多边形的周长。从正六边形一直计算到九十六边形，计算结果是

。

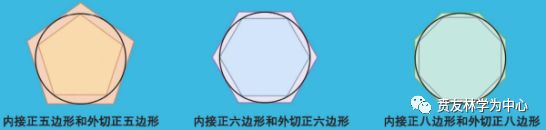
魏晋时期数学家刘徽（225-295）用割圆术来计算圆周率，“割之弥细，所失弥少。割之又割，以至不可割，则与圆合体，而无所失矣”，得出π=3.14。

南北朝的祖冲之（429-500）认为刘徽求得的结果还不够精密，继续推算出3.1415926