发明数学 创造数学

像数学家一样思考 数学精彩观念的诞生

数学可以越学越容易吗？ 贞元数学告诉你：当然可以！

编者按

精彩的核心观念建构，怎么能是个别学生的专属呢？

本期，我们继续推送八年级river班级 宜镁小作者的勾股定理探索之旅，快来围观吧！

勾股定理的探索-3

周宜镁

在我们所学习过的几何图形中，三角形属于比较特殊的一类。三角形可以分为锐角三角形，直角三角形和钝角三角形。其中直角三角形我们虽然已经有过了最基本的探索，如面积，内角和，两边之和大于第三边......但是直角三角形还有很多需要我们探究的“秘密”。

让我们先思考直角三角形具有哪些性质呢？我首先想到的是直角三角形中的两个锐角一定互余；SSA对于直角三角形的全等证明是有效的；而且我也能顺利地证明我的猜想是正确的，我就不详细地解释了，因为咱们今天的核心主题并不是这个，而是研究直角三角形 边的性质，除了两边之和大于第三边，两边差小于第三边，还有其它的性质吗？

所以我们现在就要围绕着直角三角形的三条边来展开一些研究。可是当你随手画出几个直角三角形的时候，即使测量出它的三条边的长度，这些数据也并不能给你很准确的猜想，你也发现不了它们的这三条边之间有什么特殊的联系。后来，老师让我们分别计算两条直角边的平方与斜边的平方有什么联系。通过计算，我仅仅发现了两条直角边的平方和大约等于斜边的平方。也许是因为在白纸上画出来的图不准确，且在用尺子测量时一定会产生人工误差，也就是导致无法有什么好的猜想。

那我们该如何避免这种人工误差呢？我当时就想到，肯定需要用一个统一的计量单位来计算三角形的三条边的长度，如何让单位都是一样的呢？最方便的办法就是格子图了。

可是这样画出来一个三角形好像还是没有思路，因为它的直角边是整数了，可是斜边又不是了。在老师的提醒下，我们尝试在它的旁边加上一些图形。那么两直角边的平方和就 转换成了两个小正方形的面积，斜边的平方就转换成了大正方形的面积，那么 两个以直角三角形的直角边为边长的小正方形的面积之和有可能等于以斜边为边长的正方形的面积吗？于是，我首先算出那两个小正方形的面积，如果按照方格纸上一格为一个单位计算的话，两个小正方形的面积都是3²。

那么那个大的正方形面积又要怎么计算呢？它的边长并不是整数呀，没有办法数啊？难道需要将格子拆开一个个去拼吗？于是我开始思考更加简单的方法，然后突然想到了将这个大的正方形切割成几块，看看能不能将它的面积算出来。首先想到的方法就是 切割成两个大小完全相等的等腰三角形。

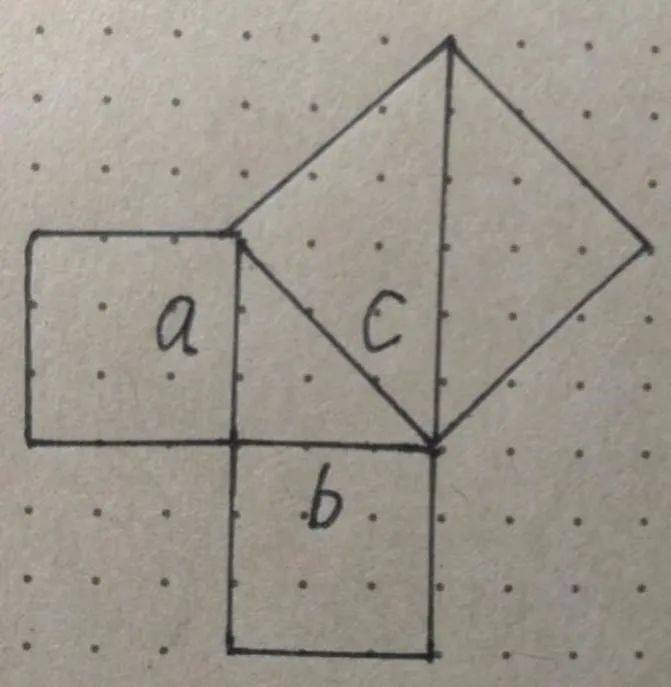
如上图，将那个大的正方形切成两个相同的三角形，然后再通过数数，可以得到三角形的底和高，这样就能算出这个正方形的面积了。这个正方形的面积应该是6×3×(1/2)×2=18。唉，突然发现了什么？这两个小正方形的面积相加，就等于这一个大正方形的面积。或者说用另一种说法， 直角三角形的两条直角边的平方相加就等于斜边的平方？在这里大概我们就能够意识到，这可能就是一个全新的发现，关于直角三角形的三条边的新规律。

可是我们现在只是单纯地发现了这一个特例，是否能够将这定为一个定理，或者说就能够得出了一个确切的结论，保证它具有普遍性呢？明显是不能的，这有可能只是一个特例，因为我们是以具体的数字来计算的，并不具有普遍性，也不足以成为一个定理。那么我们接下来要做的就是通过具有普遍性的方法来验证我们的这个猜想是否是正确的。

那我们该如何来验证呢？是在纸上画上很多个直角三角形然后去计算吗？肯定是不行的，因为只要这三条边的长度足以让这个三角形构成一个直角三角形，那么这三条边就有可能是任何数字，试的话肯定是永远也试不完的，我们需要用一种最具有 普遍性的方法，也就是能够代表所有数字的方法。而这个时候最好的方法莫过于用字母来表达。我们的猜想用字母表示为a²＋b²＝c²，那么我们是否有办法验证这个等式是否成立呢？

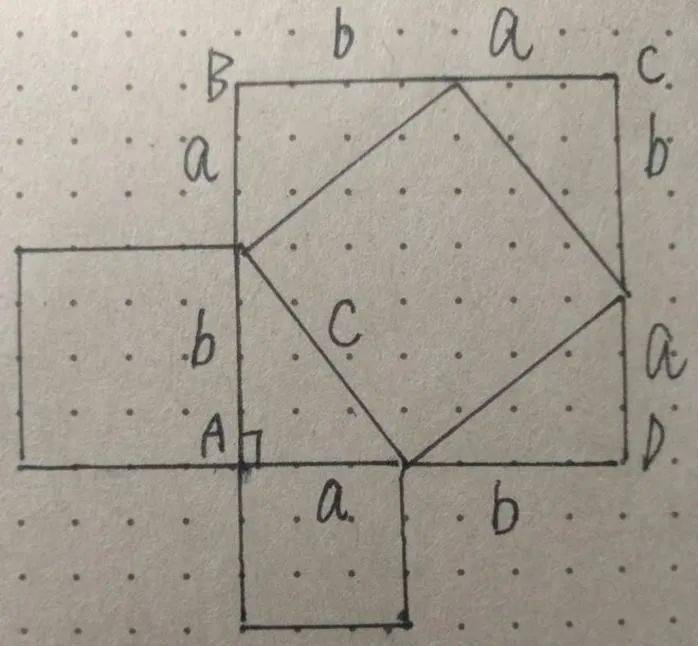
首先图中的这个最大的正方形ABCD用什么方式来表示呢？这个正方形的边长其实就是（a＋b），所以这个正方形的面积自然也就是（a＋b）²。我们可以知道图中的大正方形还可以分割成4个完全相同的直角三角形，所以它们的面积之和就是(1/2)ab×4，也就是2ab。那么大正方形ABCD的面积也可以表示为2ab+c²那么可以得到：（a＋b）²=2ab+c²，最终化到最简的结果是什么？a²＋b²＝c²。于是，我们就成功的用字母和代数式证明了这个猜想的正确性及普遍性了。

而这个时候也该揭晓答案了，其实这个猜想就是著名的勾股定理，文字语言表示就是三角形的两条直角边平方之和等于三角形中斜边的平方，符号语言就是a²＋b²＝c²。

所以你现在知道该如何通过推理得到勾股定理了吗？是不是特别好玩呀！

指导老师|宋亚男