线性代数是处理矩阵和向量空间的数学分支，在现代科学的各个领域都有应用。由于费马和笛卡尔的工作，线性代数基本上出现于十七世纪。直到十八世纪末，线性代数的领域还只限于平面与空间。十九世纪上半叶才完成了到n维向量空间的过渡,矩阵论始于凯莱，在十九世纪下半叶，因当时对其充分的研究和探索而使其达到了它的顶点。1888年，皮亚诺以公理的方式定义了有限维或无限维向量空间。托普利茨将线性代数的主要定理推广到任意体上的最一般的向量空间中。线性映射的概念在大多数情况下能够摆脱矩阵计算而引导到固有的推理，即是说不依赖于基的选择。不用交换体而用未必交换之体或环作为算子之定义域，这就引向模的概念，这一概念很显著地推广了向量空间的理论和重新整理了十九世纪所研究过的情况。

“代数”这一个词在中国出现较晚，在清代时才传入中国，当时被人们译成“阿尔热巴拉”，直到1859年，清代著名的数学家、翻译家李善兰才将它翻译成为“代数学”，之后一直沿用。

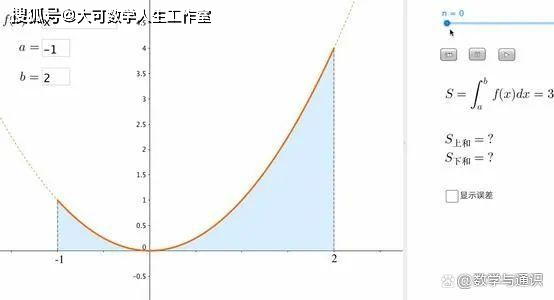
线性代数是讨论矩阵理论、与矩阵结合的有限维向量空间及其线性变换理论的一门学科。主要理论成熟于十九世纪，而第一块基石（二、三元线性方程组的解法）则早在两千年前出现。

线性代数在数学、物理学和技术学科中有各种重要应用，因而它在各种代数分支中占居首要地位。

在计算机广泛应用的今天，计算机图形学、计算机辅助设计、密码学、虚拟现实等技术无不以线性代数为其理论和算法基础的一部分。

该学科所体现的几何观念与代数方法之间的联系，从具体概念抽象出来的公理化方法以及严谨的逻辑推证、巧妙的归纳综合等，对于强化人们的数学训练，增益科学智能是非常有用的。

随着科学的发展，我们不仅要研究单个变量之间的关系，还要进一步研究多个变量之间的关系，各种实际问题在大多数情况下可以线性化，而由于计算机的发展，线性化了的问题又可以计算出来，线性代数正是解决这些问题的有力工具。

线性（linear）指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数，非线性（non-linear）则指不按比例、不成直线的关系，一阶导数不为常数。线性代数起源于对二维和三维直角坐标系的研究。在这里，一个向量是一个有方向的线段，由长度和方向同时表示。这样向量可以用来表示物理量，比如力，也可以和标量做加法和乘法。这就是实数向量空间的第一个例子。

现代线性代数已经扩展到研究任意或无限维空间。作为证明定理而使用的纯抽象概念，向量空间（线性空间）属于抽象代数的一部分，而且已经非常好地融入了这个领域。一些显著的例子有：不可逆线性映射或矩阵的群，向量空间的线性映射的环。线性代数也在数学分析中扮演重要角色，特别在向量分析中描述高阶导数，研究张量积和可交换映射等领域。向量空间是在域上定义的，比如实数域或复数域。线性算子将线性空间的元素映射到另一个线性空间（也可以是同一个线性空间），保持向量空间上加法和标量乘法的一致性。所有这种变换组成的集合本身也是一个向量空间。如果一个线性空间的基是确定的，所有线性变换都可以表示为一个数表，称为矩阵。对矩阵性质和矩阵算法的深入研究（包括行列式和特征向量）也被认为是线性代数的一部分。我们可以简单地说数学中的线性问题——那些表现出线性的问题——是最容易被解决的。比如微分学研究很多函数线性近似的问题。在实践中与非线性问题的差异是很重要的。线性代数方法是指使用线性观点看待问题，并用线性代数的语言描述它、解决它（必要时可使用矩阵运算）的方法。这是数学与工程学中最主要的应用之一。

而我们现在学的线性代数主要分为行列式，矩阵，线性方程组，n维向量空间，矩阵相似对角形，二次型及线性变换。

在线性代数中，线性方程组是基础部分，也是一个重要部分。行列式是研究线性方程组的一个重要工具。它是人们从解方程组的需要中建立起来的，它在数学本身及其他科学分支（如：物理学，力学等）中都有广泛的应用，已经成为近代数学和科技中不可缺少的工具之一。

矩阵是从许多实际问题中抽象出来的一个数学概念，是线性代数的重要内容之一，它贯穿线性代数的各个部分。矩阵是许多学科中常用的数学工具，它在自然学科、工程技术和国民经济的许多领域中都有着广泛应用。线性方程组的理论在线性代数中起着重要作用。事实上，线性代数的许多问题都相当于研究线性方程组。如线性方程组的克莱姆法则，其法则的使用是有条件的：（1）未知量的个数与方程个数相等；（2）系数行列数不等于零。可是在许多问题中所遇到的方程组并不满足上述两个条件。这就促使我们有必要进一步讨论一般的线性方程组。

线性方程组的解法，早在中国古代的数学著作《九章算术 方程》中已作了比较完整的论述。其中所述方法实质上相当于现代的对方程组的增广矩阵施行初等行变换从而消去未知量的方法，即高斯消元法。在西方，线性方程组的研究是在17世纪后期由莱布尼茨开创的。他曾研究含两个未知量的三个线性方程组组成的方程组。麦克劳林在18世纪上半叶研究了具有二、三、四个未知量的线性方程组，得到了前面提到的克莱姆法则的结果。克莱姆不久也发表了那个法则。18世纪下半叶，法国数学家贝祖对线性方程组理论进行了一系列研究，证明了n元齐次线性方程组有非零解的条件是系数行列式等于零。

19世纪，英国数学家史密斯 (H.Smith) 和道奇森 (C-L.Dodgson) 连续研究线性方程组理论，前者引进了方程组的增广矩阵和非增广矩阵的概念，后者证明了方程组相容的充要条件是系数矩阵和增广矩阵的秩相同。这正是现代方程组理论中的重要结果之一。

大量的科学技术问题，最终往往归结为解线性方程组。因此在线性方程组的数值解法得到进展的同时，线性方程组解的结构等理论性工作也取得了令人中意的进展。现在，线性方程组的数值解法在运算数学中占有重要地位。

在许多实际问题的研究中，常需要将一个矩阵化为相似对角形的问题。二次型起源于解析几何中化二次曲线和二次曲面的方程为标准形的问题。它的理论在数学、物理及其他许多学科中都有重要应用。变换是数学上的一个重要且有用的概念，线性变换同向量空间一样是线性代数的核心内容，它是反映线性空间元素之间最基本的线性关系。

高等数学是理工科、经济、农类乃至部分文科专业的公共基础课，线性代数是高等数学的重要组成部分，其主要内容都是信息时代各类人才应该掌握的基本工具。所以我们要好好学习这门课，好好利用线性代数。

下面再拓展一下，谈一谈从解方程到群论。求根问题是方程理论的一个中心课题。16世纪，数学家们解决了三、四次方程的求根公式，关于更高次方程的求根公式是否存在，成为当时的数学家们探讨的又一个问题。这个问题花费了许多数学家们大量的时间和精力。经历了多次失败，但总是摆脱不了逆境。

到了18世纪下半叶，拉格朗日认真总结分析了前人失败的体会，深入研究了高次方程的根与置换之间的关系，提出了预解式概念，并预见到预解式和各根在排列置换下的形式不变性有关。但他最终没能解决高次方程问题。拉格朗日的弟子鲁菲尼 (Ruffini,1765-1862) 也做了许多努力，但都以失败告终。高次方程的根式解的讨论，在挪威杰出数学家阿贝尔那儿取得了大进展。阿贝尔 (N.K.Abel,1802-1829) 只活了27岁，他一生贫病交加，但却留下了许多创造性工作。1824年，阿贝尔证明了次数大于四次的一般代数方程不可能有根式解。但问题仍没有完全解决，因为有些专门方程能够用根式求解。因此，高于四次的代数方程何时没有根式解，是需要进一步解决的问题。这一问题由法国数学家伽罗瓦全面透彻地给予解决。

伽罗瓦 (E.Galois,1811-1832) 认真研究了拉格朗日和阿贝尔的著作，建立了方程的根的“容许”置换，提出了置换群的概念，得到了代数方程用根式解的充分必要条件是置换群的自同构群可解。从这种意义上，我们说伽罗瓦是群论的创立者。伽罗瓦出身于巴黎邻近一个富裕的家庭，幼时受到良好的家庭教育，只惋惜，这位天才的数学家英年早逝，1832年5月，由于政治和爱情的纠葛，在一次决斗中被打死，年仅21岁。

置换群的概念和结论是最终产生抽象群的第一个重要来源。抽象群产生的第二个重要来源则是戴德金(R.Dedekind,1831-1916) 和克罗内克 (L.Kronecker,1823-1891) 的有限群及有限交换群的抽象定义以及凯莱 (A.Kayley,1821-1895) 关于有限抽象群的研究工作。另外，克莱因 (F.Clein,1849-1925) 和庞加莱 (J-H.Poincare,1854-1912) 给出了无限变换群和其他类型的无限群，19世纪70年代，李 (M.S.Lie,1842-1899) 开始研究连续变换群，并建立了连续群的一般理论，这些工作构成抽象群论的第三个重要来源。

1882-1883年，迪克 (W.vondyck,1856-1934) 的论文把上述三个重要来源的工作纳入抽象群的概念之中，建立了（抽象）群的定义。到19世纪80年代，数学家们终于成功地概括出抽象群论的公理体系。

20世纪80年代，群的概念被认为是数学及其许多应用中最普遍的概念之一。它不但渗透到诸如几何学、代数拓扑学、函数论、泛函分析及其他许多数学分支中而起着重要的作用，还形成了一些新学科如拓扑群、李群、代数群等，它们还具有与群结构相联系的其他结构，如拓扑、解析流形、代数簇等，并在结晶学、理论物理、量子化学以及编码学、自动机理论等方面，都有重要作用。

来自：数学与通识