数学作为一门古老而又现代的学科，对于我们的生活有着深远的影响。而其中，阿波罗尼奥斯的《圆锥曲线论》更是为后世的科学家和数学家提供了重要的启示和思路。本文将仔细探讨《圆锥曲线论》的影响，并着重讨论其在现实生活中的应用。

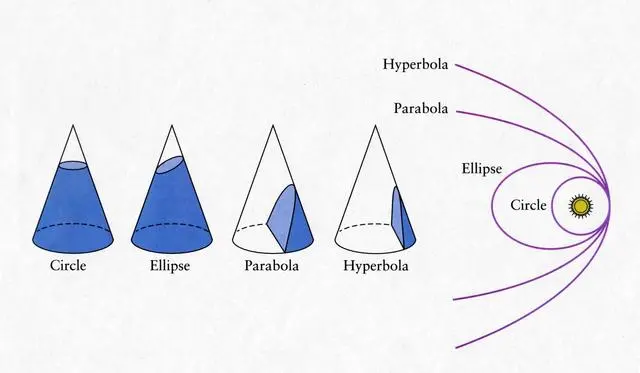
一、圆锥曲线的基本原理

1. 椭圆的魅力

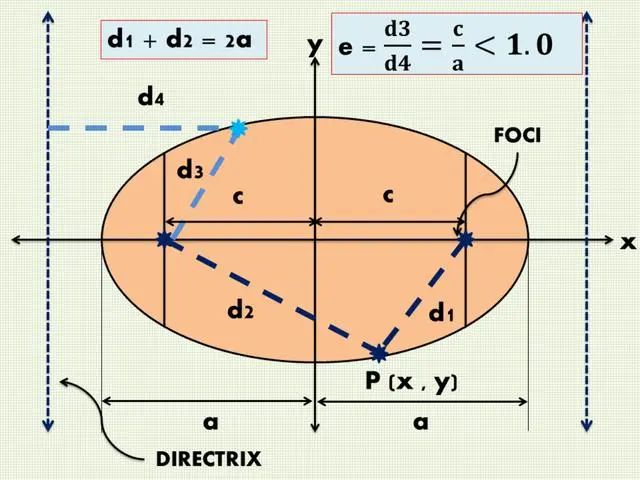
椭圆是一种非常迷人的几何图形，它具有许多有趣的特性。首先，椭圆的定义是平面上到两个定点（焦点）的距离之和等于常数的点的集合。这个常数称为椭圆的长轴，而两个焦点之间的距离是椭圆的短轴。通过改变焦点之间的距离，我们可以得到各种不同形状的椭圆。

除了其独特的形状，椭圆还具有许多重要的性质。例如，椭圆上任意一点到两个焦点的距离之和是常数。这个性质在光学中有广泛应用，例如反射望远镜和卫星通信。此外，椭圆还与椭圆积分、行星运动和天体力学等领域密切相关。

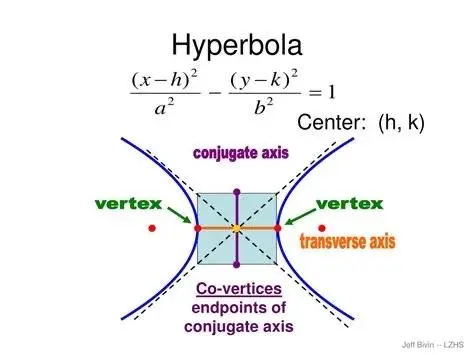
2. 双曲线的神秘

与椭圆相比，双曲线具有截然不同的形状和性质。双曲线的定义是平面上到两个定点（焦点）的距离之差等于常数的点的集合。这个常数称为双曲线的距离差。与椭圆不同，双曲线具有两个分离的曲线分支，且没有中心对称性。

双曲线的特殊性质使其在许多领域得到广泛应用。例如，电磁波的传播就可以通过把双曲线看作反射点的轨迹来解释。此外，双曲线还与超越函数、流体力学和相对论等领域相关联。

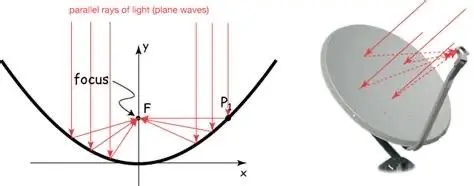
3. 抛物线的优雅

抛物线是圆锥曲线中最简单、最常见的一种。它的定义是平面上到一个定点（焦点）的距离等于另一个定点到一条直线（准线）的距离的点的集合。这个准线与焦点之间的距离称为抛物线的焦距。

抛物线具有许多独特的性质，使它们在现实生活中得到广泛应用。例如，球体的抛物线运动可以通过抛物线的形状和对称性来描述。此外，抛物线还与天体力学、天桥设计和反射式太阳能收集器等领域相关。

二、圆锥曲线的数学与应用

1. 笛卡尔坐标系的崛起

笛卡尔坐标系是数学中一项重要的发明，它将几何问题转化为代数问题，极大地推动了数学的发展。笛卡尔坐标系利用两条垂直的坐标轴（x轴和y轴）来表示平面上的点，从而将几何图形与代数方程联系起来。

通过将圆锥曲线的定义转化为代数方程，我们可以用坐标系方程来描述和分析这些曲线。例如，椭圆的坐标系方程为(x/a)^2 + (y/b)^2 = 1，其中a和b分别是椭圆的半长轴和半短轴。

2. 微积分的奇迹

圆锥曲线论对微积分的发展产生了深远的影响。众所周知，微积分是研究函数变化率和曲线面积的数学分支。牛顿和莱布尼茨在发明微积分的过程中，受到了圆锥曲线论的启发。

通过对圆锥曲线的导数和积分进行研究，牛顿和莱布尼茨成功地建立了微积分的基本概念和定理。这使得微积分成为许多科学领域的核心工具，如物理学、工程学和经济学等。

三、圆锥曲线在实际生活中的应用

1. 天文学之谜

圆锥曲线在天文学中扮演着重要角色，帮助我们研究行星运动和宇宙奥秘。开普勒定律描述了行星在椭圆轨道上运动的规律，这一定律直接源于椭圆的性质。同时，牛顿的万有引力定律也利用了椭圆和双曲线的性质，解释了行星之间的相互引力。

通过观测天体的位置和轨迹，并结合圆锥曲线的数学模型，我们能够预测天体的运动、计算轨道参数以及解释一些天文现象，如彗星的轨道和恒星的视位置。

2. 工程与建模

圆锥曲线在工程学中有着广泛的应用。例如，在桥梁设计中，拱形结构常常使用为主要承重构件，因为拱形能够将载荷传递到基础上，具有较高的稳定性。拱形的截面形状就是一个抛物线或椭圆。

此外，隧道设计中的截面形状也可以采用圆锥曲线，以减少地质力对隧道结构的影响。太阳能聚焦器利用抛物面的反射特性来将太阳能集中到一个点上，以产生热能。

《数学之书》数学已经渗入每一个科学领域，并且在生物学、物理、化学、经济、社会学和工程等方面扮演着无法替代的角色。我们可以用数学说明夕阳色彩分布的情况，也可以用来说明人类的大脑结构，可以帮助我们探索比原子还小的量子世界，也可以帮助我们描绘遥不可及的银河系。

在现实世界运用的著名计算公式和数学定理背后隐藏着数学家们一生的传奇故事。跟随皮寇弗踏上这趟数学之旅，探索数学历史上最重要的250个里程碑事件，从蚂蚁计数到第一把算盘，从发现计算机创造的碎形到寻找新的维度空间。

结语

通过本文的深入探讨，我们详细了解了圆锥曲线的基本知识、性质和应用。从椭圆、双曲线到抛物线，每个曲线都有其独特的魅力和应用领域。笛卡尔坐标系和微积分为我们更好地理解和分析圆锥曲线提供了强有力的工具。天文学和工程学中的实际应用进一步展示了圆锥曲线在现实生活中的重要性。相信通过这段奇妙之旅，读者们将更加深入地理解和欣赏数学的美妙世界！