一、萌芽

早在公元前5世纪至公元前4世纪，古希腊的数学家还在痴迷于“化圆为方”、“立方倍积”和“三等分任意角”三大不可能问题。尽管他们没有完成这些现在看来是已经不可能的问题，但是在研究这些问题中，也有了意外的收获。古希腊数学家梅内克缪斯在解决“立方倍积”问题时，用平面截不同的圆锥，发现圆锥曲线。

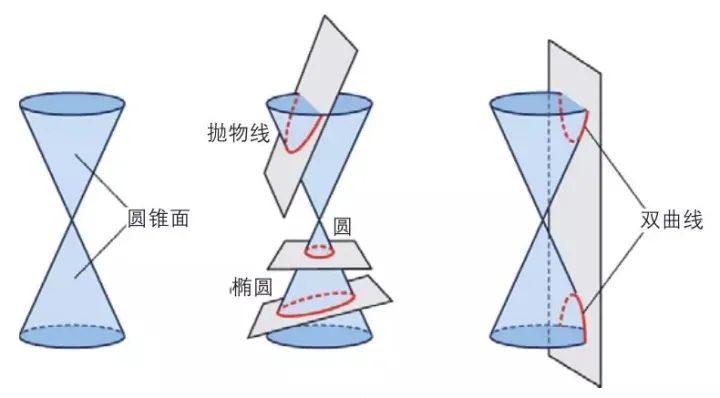
关于圆锥曲线的发现还有一种说话，圆锥曲线可能是在制作日晷时被发现的，但关于日晷的制作方法，现已失传，这一说话也无法考证。

二、奠基

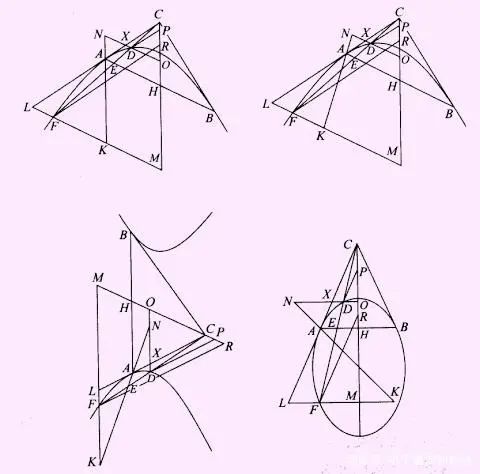
阿波罗尼斯是第一个依同一个圆锥的截面来研究圆锥曲线的人，也是第个发现双曲线有两支的人，他按照欧几里得《几何原本》公理演绎的方式把圆锥曲线理论系统化，所著《圆锥曲线论》从“平面斜截圆锥”出发，运用纯几何方法，证明了487个命题，含有许多独到新颖的创见，把圆锥曲线的性质几乎网罗殆尽。阿波罗尼斯的《圆锥曲线论》与欧几里得的《几何原本》同被誉为古希腊几何巅峰之作。他本人也被誉为古希腊“伟大的几何学家”。

《圆锥曲线》8卷，共487个命题。

第 1 卷，圆锥曲线的定义、性质；

第 2 卷，双曲线渐近线的作法、性质，由此引入共轭双曲线，圆锥曲线切线的作法；

第 3 卷，圆锥曲线与其切线、直径所成图形的面积，极点极线的调和性，焦点的性质；

第 4 卷，极点极线的其它性质，各种位置的圆锥曲线可能有的交点数；

第 5 卷，从特定点到圆锥曲线所能作的最长线和最短线；

第 6 卷，全等圆锥曲线、相似圆锥曲线及圆锥曲线弓形；

第 7 卷，有心圆锥曲线两共轭直径；

第 8 卷，失传。

《圆锥曲线》现在的版本中，前4卷是从12至13世纪的希腊手稿本复制的，其后的3卷是从1290年阿拉伯译本转译的，第8卷已失传，现为17世纪的哈雷根据帕普斯书中的启示而搞出来的一个代替稿。

三、停滞

由于阿波罗尼斯《圆锥曲线论》几乎圆锥曲线的性质收集殆尽，在阿波罗尼斯的《圆锥曲线》问世后的 13 个世纪里，整个数学界对圆锥曲线的研究没有什么进展。公元 11 世纪，中亚数学家海雅姆利用圆锥曲线来解三次方程，而对圆锥曲线本身并没有深入的研究。古希腊时期还没有代数的符号体系和坐标，阿波罗尼斯的证明是建立在纯粹的论证几何基础上的，并用文字表述证明的过程与结论，这是后人很难读懂其著作的原因之一。

四、突破

直到16世纪末，开普勒揭示出行星按椭圆轨道绕太阳运行，是圆锥曲线摆脱圆锥而成为自然界中物体运动的普遍形式。伽利略得出斜抛运动的轨道是抛物线，突破了静态圆锥曲线的观念。人们发现圆锥曲线不仅是依附在圆锥上的静态曲线也是自然界物体运动的普遍形式，于是，对圆锥曲线的处理方法开始有了变化。

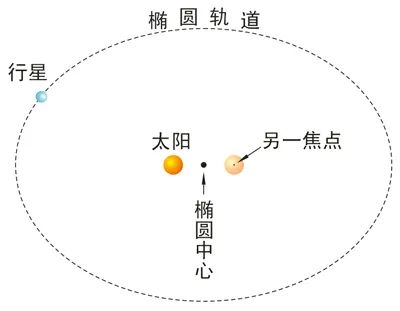
1579年，蒙蒂采用焦点、定长的方式，定义了椭圆，改变以往平面截圆锥的定义方式；开普勒关于几何图形连续变换的思想，为圆锥曲线的统一定义奠定了基础。

17世纪，笛沙格、帕斯卡和德•拉•希尔利用本来为画家提供帮助的投射和截影的方法来研研究圆锥曲线，并得出了一些关于圆锥曲线的特殊的定理。

五、开拓

17世纪笛卡尔和费尔马的《空间与平面轨迹入门》，使解析几何走向数学舞台，人们对圆锥曲线的研究朝着解析法的方向发展。解析几何的创立，使人们对圆锥曲线的认识进入了一个现阶段。即通过建立坐标系，得出圆锥曲线的方程，再利用方程研究锥曲线的性质，摆脱了几何直观获得对圆锥曲线研究的高度概括与统一。这时，对圆锥曲线的研究方法既不同于阿波罗尼斯，又不同于笛沙格，而是朝着解析方法的方向发展。

六、完备

18世纪，牛顿、贝努利等先后提出不同的坐标系，尤其影响深刻的是极坐系，随着坐标系的系统化，关于圆锥曲线性质研究逐渐系统化起来。欧拉1745年发表的《分析引纶》，被誉为解析几何发展史上的重要著作，系统地研究了圆锥曲线的各种情形，并证明通过坐标变换，一定可以把任何圆锥曲线化为某种标准形式，欧拉之后，三维解析几何的研究蓬勃开展，由圆锥曲线导出了圆锥曲面，至此，关于圆锥曲线的理论被广泛应用，直至今天。