勾股数判定定理

一个实部与虚部皆为整数且皆不为零的复数，当与其共轭复数之积是一个完全平方数时，这个复数是勾股数。

实数范围内的勾股定理是复数勾股定理的特殊形式。勾股定理反映的是三个复数模长之间关系的定理。在复平面上，仅有相互垂直且实部与虚部有特定关系的复数才满足勾股定理。

具体地说就是任意一个复数 a+bi，必定存在 b-ai 与它垂直，以 a+bi 与 b-ai 的模长为边可作一直角三角形，这个直角三角形的斜边是一个复数，且这个斜边是由 a+bi 与 b-ai 的模唯一确定的。假定它是 c+di ，则 a+bi 的模长的平方与 b-ai 的模长的平方之和等于 c+di 的模长的平方，可以总结成下面这个公式。因为这个直角三角形的三条边的长度可以分别看作对应复数的模长，于是写成下面这种形式，norm 代表复数的模长。

norm(m(a+bi))^2+norm(n(b-ai))^2＝

norm(c+di)^2 公式一

虽然勾股定理在实数范围内普遍成立，但为了与传统意义上的勾股定理保持一致，式中所有的字母都取整数且不能为零。

m(a+bi) 仍为复数，norm(m(a+bi))^2表示 m(a+bi) 这个复数的模长的平方，余类推。

式中，m，n 是系数，它能够保证这些复数的模长都是整数。并非所有相互垂直的复数都满足上式，只有实部与虚部存在上述关系时才成立。即只有象 a+bi 与 b-ai 这样的一对复数才满足勾股定理。在这里，a 和b 是可以相等的，即 a+ai 与 a-ai 这样的一对复数也满足勾股定理。

由以上分析知道，在某些条件满足的前题下，勾股定理在复数域内也是成立的。举例如下：

3+3i 与 3-3i 互相垂直

(norm(3+3i))^2+(norm(3-3i))^2＝6^2

说明：分别以 3+3i 和 3-3i 的模长为直角边作一直角三角形，斜边长度等于6。

3(3+4i) 与 4(4-3i) 互相垂直

norm(3(3+4i))^2+norm(4(4-3i))^2＝

25^2

说明：分别以 3(3+4i) 和 4(4-3i) 的模长为直角边作一直角三角形，斜边长度等于25。余类推。

norm(21(5+12i))^2+norm(20(12-5i))^2＝377^2

……

对于任意一个复数 a+bi ，由于复数包括实数和纯虚数，因此，复数 a+bi 可以看成是复数 a 与复数 bi 的和。由于a和 bi 相互垂直，且 a 的模是 a，bi 的模是 bi，所以 a+bi 的模的平方等于 a的模的平方加上 bi 的模的平方，即

norm(a)^2+norm(bi)^2＝norm(a+bi)^2

上式表明，a+bi 的模的平方等于 a 的模的平方加 bi 的模的平方。推导如下

先给出两对复数 a+0i 和0-ai，0+bi 和 b-0i

norm(a+0i)^2+norm(0-ai)^2＝norm(a-ai)^2

norm(0+bi)^2+norm(b-0i)^2=

norm(b+bi)^2

由于 a 的 模长与 -ai 的模长相等，即

norm(a)^2+norm(-ai)^2＝2norm(a)^2

同理，norm(bi)^2+norm(b)^2＝

2norm(bi)^2

norm(a-ai)^2+norm(b+bi)^2=

2norm(a+bi)^2，所以

2norm(a)^2+2norm(bi)^2=2norm(a+bi)^2

等式两边同除以2，得

norm(a)^2+norm(bi)^2=norm(a+bi)^2

这个式子就是任意复数模长的计算公式。

因此，实数的勾股定理是复数的勾股定理的特殊形式。

(3+i)^2+(3-i)^2＝4^2 不满足勾股定理

，因为 3+i 与 3-i 不垂直。

(norm(3+3i))^2+(norm(3-3i))^2＝6^2

满足勾股定理，因为 3+3i 与 3-3i 互相垂直，因此，以 3+3i 与 3-3i 为直角边的三角形，斜边长度等于6。

(norm(3+4i))^2+(norm(4-3i))^2＝50

不满足勾股定理，因为以 3+4i 和 4-3i

为直角边的直角三角形，斜边是√50，不是整数(文中所有代表数的字母都代表整数)。

象这样相互垂直的两个复数的平方和等于0。

a+bi 与 b-ai 互相垂直

a+ai 与 a-ai 互相垂直

(3+4i)^2+(4-3i)^2＝0

(a+bi)^2+(b-ai)^2＝0

(4-3i)^2+(-3-4i)^2＝0

......

下面再举几例：

norm(3(3+4i))^2+norm(4(4-3i))^2＝

25^2

norm(3)^2+norm(4i)^2＝norm(3+4i)^2

(norm(21(5+0i))^2+norm(3(0+12i))^2)＝111^2

上式还可以写成

21^2×5^2+3^2×12^2=111^2，得

441^2×5^2+9×12^2=111^2

……

总结得出，m•a^2+n•b^2＝c^2，这就是实数范围内勾股定理的一般形式。

下面这个例子说明了系数 m，n 在公式一中的作用。

norm(21(5+12i))^2+norm(3(12-5i))^2＝275.7716447^2

norm(21(5+12i))^2+norm(20(12-5i))^2＝377^2

调整公式一中的系数，可以使得公式右端的数能够写成整数的平方的形式。

勾股定理反映的是复数之间的关系，从此刻起，我用满足勾股定理的复数代指勾股数，例如，勾股数 (3,4,5)，等价于复数 3+4i。勾股数 a+bi 的模的平方等于复数 a 的模的平方与复数 bi 的模的平方之和，这已经在前文提到过了。

下面给出几个与勾股数有关的定理。

① 勾股数的无穷乘积是勾股数。

② 勾股数的 N 次方是勾股数。

③ 非勾股数的平方一定是勾股数。

④ 勾股数的整数倍仍然是勾股数。

⑤ 非勾股数的偶数次幂是勾股数，勾股数的奇数次幂不是勾股数。

⑥ 由两个勾股数与一个非勾股数构成的等比数列中，非勾股数是等比中项。

(3+4i)(4+7i)(5+12i)

(4+7i)/(3+4i)＝1.6+0.2i

(5+12i)/(4+7i)＝1.6+0.2i

(4+7i)²＝(3+4i)(5+12i)

norm(4+7i)/norm(3+4i)＝1.61245155

（无理数）

norm(5+12i)/norm(4+7i)＝

1.61245155…（无理数）

可见 3+4i 4+7i 5+12i 这三个复数的模长值构成了等比数列。

norm(3+4i)＝5

norm(4+7i)＝√65

norm(5+12i)＝13

即 5 √65 13 构成等比数列。

可见，实数范围内的等比数列是复数等比数列的又一特殊形式，它反映了复数模长之间的比例关系。

由于勾股定理在实数范围内成立，下面以勾股数 3+4i 为例延伸一下勾股定理。根据定理④，勾股数的整数倍仍然是勾股数，其实，把整数换成实数这一结论仍然成立。比如，0.3+0.4i 这个勾股数，它的模norm(0.3+0.4i)＝0.5，以勾股定理的常见形式写出来就是 0.3²+0.4²＝0.5²，同理可知

0.03²+0.04²＝0.05²

0.003²+0.004²＝0.005²

0.0003²+0.0004²＝0.0005²

.......

将上面这些式子用科学记数法表示成

(3E−1)²+(4E−1)²＝(5E−1)²

(3E−2)²+(4E−2)²＝(5E−2)²

(3E−3)²+(4E−3)²＝(5E−3)²

(3E−4)²+(4E−4)²＝(5E−4)²

(3E−5)²+(4E−5)²＝(5E−5)²

……

由于 E−10＝1埃＝1埃(Å)，所以

(3E−10)²+(4E−10)²＝(5E−10)²又可以写成

(3Å)²+(4Å)²＝(5Å)²，写成复数的形式就是 3Å+4Åi。

数学中有一种映射叫共形影射，又称保角映射，即直角在共形影射中仍被影射为直角，在拓扑学中定义的曲面是它的每一点有同胚于平面的邻域，因此，只要在曲面上存在直角，那么勾股定理就依然在曲面上有效。当直角三角形的边都按同一比例趋于无限小的时候，勾股定理仍然有效。勾股定理在空间变换的过程中保持形式不变，这一性质可以推广到一般形式。我猜想勾股数对方程的求解具有重要的意义。

其它几条定理我就不例举说明了，可以检验它们都是正确的，但我无法给出证明。

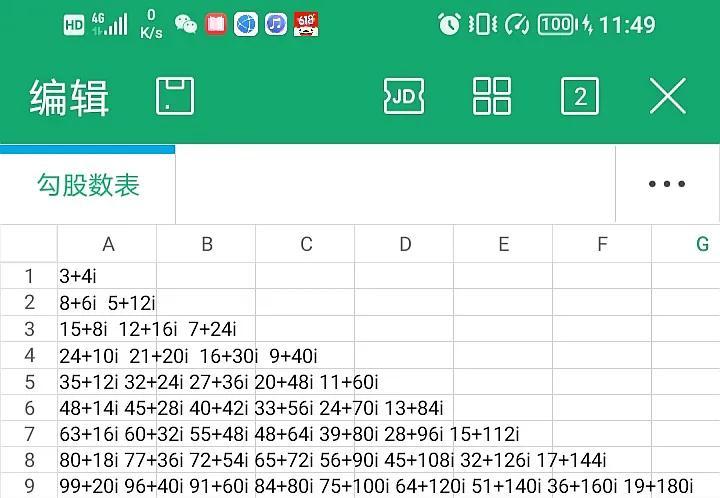
下面谈一下与勾股数有关的数列，参看下面这张图表。

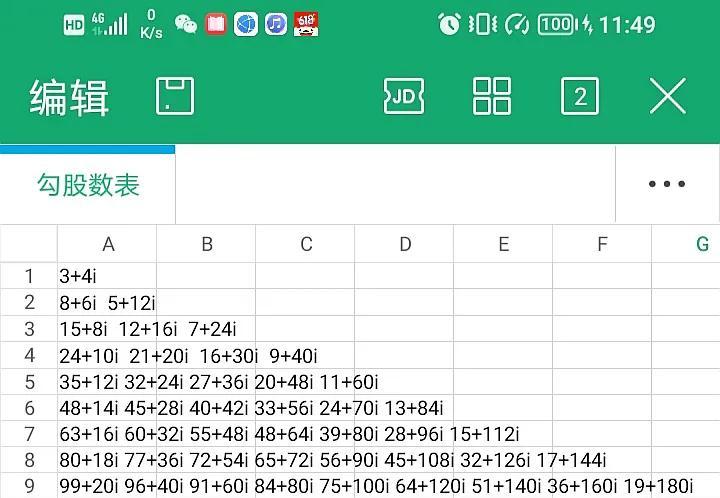
图1

表中每一行的复数都是勾股数，每一行的勾股数都与等差数列有关，即只要知道了每一行的第一个勾股数，利用等差数列运算就可以求出跟在后面的勾股数。当然这些勾股数间的运算也可以用矩阵加法运算实现。

用复数证明勾股定理

因为共轭复数的积是一个完全平方数，即 (a+bi)(a-bi)＝c^2，复数 a+bi 的模 norm(a+bi)＝√(a^2+b^2) 与共轭复数的积 (a+bi)(a-bi) 开方后相等，即 √(a^2+b^2)＝√((a+bi)(a-bi))，所以

√(a^2+b^2)＝√c^2，两边平方，得 a²+b²＝c²

勾股数的矩阵运算

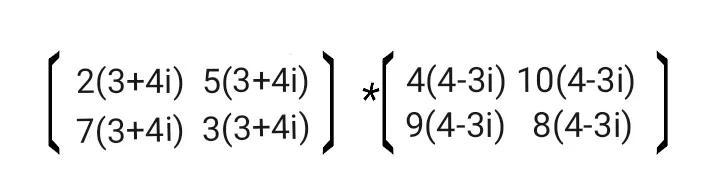
矩阵乘法运算

2(3+4i)•4(4-3i)+5(3+4i)•9(4-3i)=

1272+371i

2(3+4i)10(4-3i)+5(3+4i)8(4-3i)=

1440+420i

7(3+4i)4(4-3i)+3(3+4i)9(4-3i)=

1320+385i

7(3+4i)10(4-3i)+3(3+4i)8(4-3i)=

2256+658i

得到下面这个矩阵

乘法运算结果

将这些数再相乘或相乘后相加仍然是勾股数。

(1272+371i)(2256+658i)＝

2625514+1673952i (勾股数)

(1440+420i)(1320+385i)＝

1739100+1108800i (勾股数)

(1272+371i)(2256+658i)+(1440+420i)(1320+385i)=4364614+2782752i (勾股数)

对于任意复数，下式成立。

(a+bi)(b-ai)＝c+di

c＝2ab，d＝(a+b)(b-a)

如果矩阵中的元素都相同，下面是二阶方阵的乘法运算。

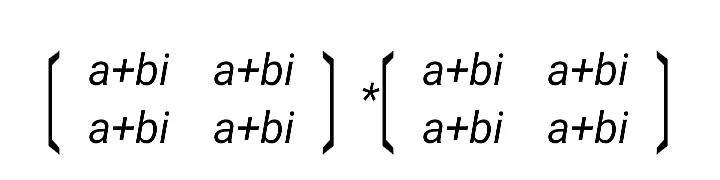
图1

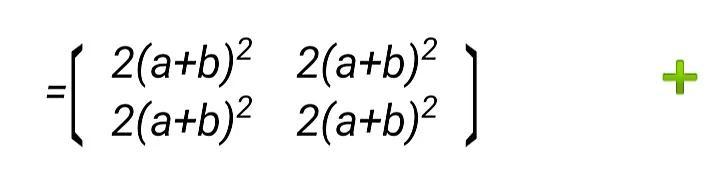
图2

令 a+bi＝n，(a+bi)²＝n²，上面的矩阵又可以写成下面的形式：

图3

把 2 提出到这个矩阵的外面，得到

图4

当 n＝1+i 时， 2n²＝2(1+i)²=4i

当 n＝2+2i 时，2n²＝2(2+2i)²=16i

当 n＝3+3i 时，2n²＝2(3+3i)²=36i

当 n＝4+4i 时，2n²＝2(4+4i)²=64i

当 n＝5+5i 时，2n²＝2(5+5i)²=100i

当 n＝6+6i 时，2n²＝2(6+6i)²=144i

当 n＝7+7i 时，2n²＝2(7+7i)²=196i

当复数 a+bi 的虚部 b＝0 时，得到

当 n＝1 时，2n²＝2×1²=2

当 n＝2 时，2n²＝2×2²=8

当 n＝3 时，2n²＝2×3²=18

当 n＝4 时，2n²＝2×4²=32

当 n＝5 时，2n²＝2×5²=50

当 n＝6 时，2n²＝2×6²=72

当 n＝7 时，2n²＝2×7²=98

这些值与原子核外电子的排布规律相同，我们发现这些数值的排列也与等差数列相关。

2+6＝8

8+10＝18

18+14＝32

32+18＝50

50+22＝72

72+26＝98

第一个加数从 2 开始与一个等差数列中的数次第相加，第二个加数从 6 开始次第与那个等差数列的公差相加。

联系原子中电子的排布，显然，我们对电子的排布规律认识的并不全面。电子在复空间中的轨道数量会翻倍。

下面说一个与勾股数有关的复变函数幂函数。前面我们提到说勾股数的 N 次幂是勾股数，这里设 z 是勾股数(复数)为一个复变量，幂函数ω＝z^α，α是一个常数，取值为任意正整数，则幂函数的值是勾股数，这是一个从勾股数空间到勾股数空间的映射。

勾股数的乘法构成一个乘法群，因为

① 勾股数的无穷乘积是勾股数。

② 满足结合律。

③ 单位元是 1。

④ 逆元是它的倒数。

所以勾股数构成了乘法群。