作用及含义
探索性因子分析是基于降维的思想,在尽可能不损失或者少损失原始数据信息的情况下,将错综复杂的众多变量聚合成少数几个独立的公共因子,这几个公共因子可以反映原来众多变量的主要信息,在减少变量个数的同时,又反映了变量之间的内在联系。
通常因子分析有三种作用:一是用于因子降维,二是计算因子权重,三是计算加权计算因子汇总综合得分
举个例子
根据某地区2021年的人均GDP、人均可支配收入等多个指标,量化评估多个省市地区的经济发展水平排名或者各指标的权重
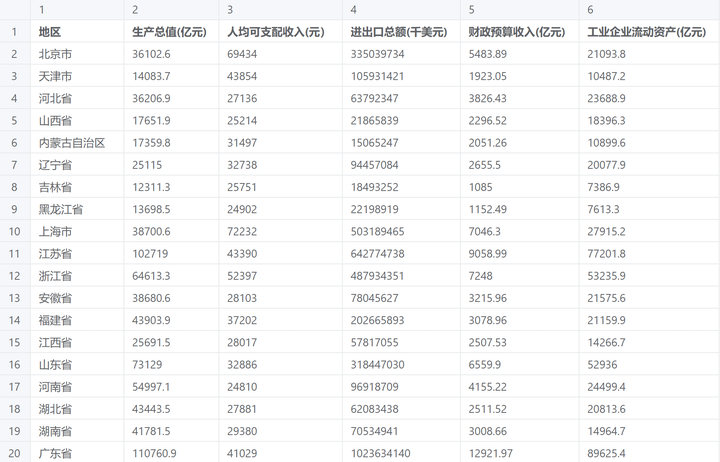
探索性因子分析数据案例操作
使用工具:免费在线版SPSS——SPSSPRO(功能免费,系统自动分析结果)
打开SPSSPRO,选择因子分析(探索性)将变量拖入框中,而后点自动分析
分析步骤
以下分析步骤源于SPSSPRO免费数据分析网站
1.首先进行KMO和Bartlett的检验,判断是否可以进行因子分析。 对于KMO值:0.9上非常合适做因子分析,0.7-0.9之间适合,0.6-0.7之间尚可,0.5-0.6之间表示差,0.5下应该放弃;通KMO值检验可以说明是否适合使用因子分析;
2.对于 Bartlett的检验(p < 0.05,严格来说p < 0.01),若显著性小于0.05或0.01,拒绝原假设,则说明可以做因子分析,若不拒绝原假设,则说明这些变量可能独立提供一些信息,不适合做因子分析;
3.通过分析方差解释表格和碎石图,确定因子的数量
方差解释表格主要是看因子对于变量解释的贡献率(可以理解为究竟需要多少因子才能把变量表达为100%),如果太低(如低于60%)则需要调整因子数据;
碎石图的作用是根据特征值下降的坡度来确认需要选择的因子个数,这两者结合可用于确认或调整因子个数;
4.通过分析因子载荷系数与热力图,可以分析到每个因子中隐变量的重要性,如研究【多金属矿体】中25种有用元素的分布规律,其中各元素视为指标,假设前文确定得到5个因子,因子1中,SO、SO2、Na2S、HS、H2S因子载荷系数较大,因此可将因子1确定为硫化物成分,以此类推,也可结合具体业务进行各因子的隐变量分析;
通过分析成分矩阵,得出因子公式;
5.基于因子载荷图通过将多因子降维成双因子或者三因子,通过象限图的方式呈现因子的空间分布。如果提取2个因子时,无法呈现三维载荷因子散点图,如果提取1个因子时,无法显示因子象限图;
6.通过分析成分矩阵,得出因子成分公式与权重;
7.输出因子分析法综合得分。
结果分析1、KMO检验和Bartlett的检验
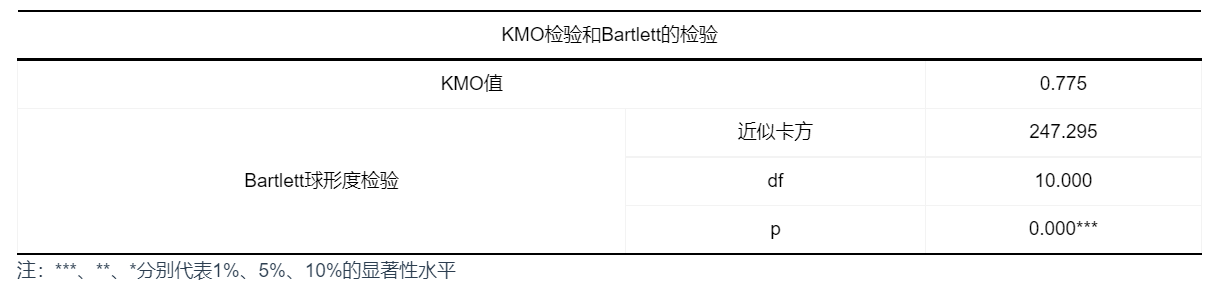
图表说明: 上表展示了KMO检验和Bartlett球形检验的结果,用来分析是否可以进行因子分析。
● 若通过KMO检验(KMO>0.6),说明了题项变量之间是存在相关性的,符合因子分析要求;
● 若通过Bartlett检验:P
智能分析KMO检验的结果显示,KMO的值为0.775,同时,Bartlett球形检验的结果显示,显著性P值为0.000***,水平上呈现显著性,拒绝原假设,各变量间具有相关性,因子分析有效,程度为一般。
2、方差解释表格
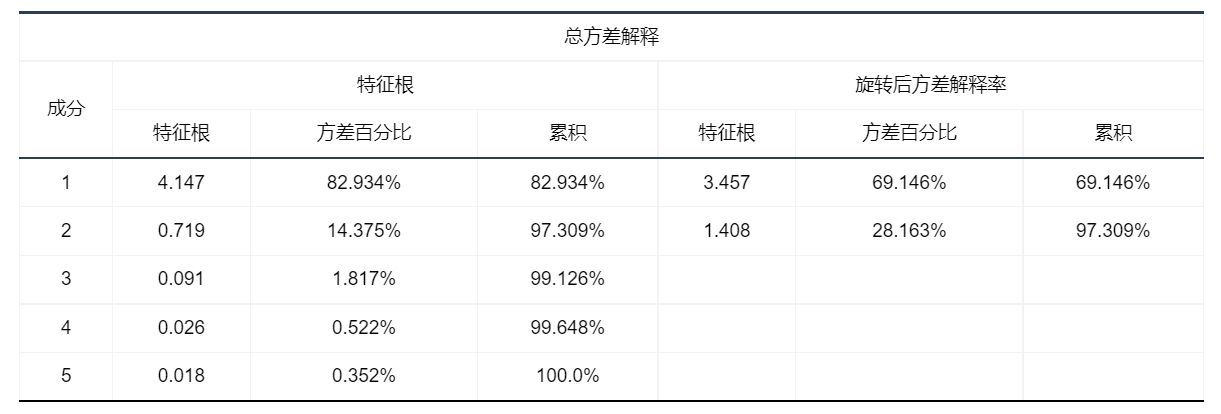
图表说明: 上表为总方差解释表格,主要是看因子对于变量解释的贡献率(可以理解为究竟需要多少因子才能把变量表达为100%),如果太低(如低于60%)则需要调整因子数量。
● 一般情况下,方差解释率越高,说明该主成分越重要,权重占比也应该越高。旋转后因子的方差解释率,特征根,方差解释率,累积方差解释率,用于求解主成分公式;
● 当因子数量设置为1时,单个因子的方差解释率不支持旋转,因此旋转后方差解释率为空。
智能分析方差解释表中,在主成分2时,总方差解释的特征根低于1.0,变量解释的贡献率达到97.309%,以上仅为参考,若特征根小于1.0临界值过大,也可以集合具体情况具体分析。
3、碎石图
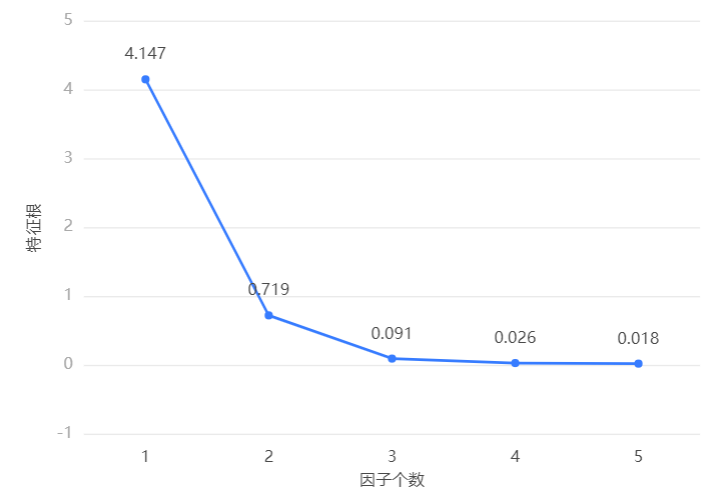
图表说明:
● 碎石图是根据各主成分对数据变异的解释程度绘制的图。其作用是根据特征值下降的坡度来确认需要选择的因子主成分个数,结合方差解释表可用于确认或调整因子主成分个数;
● 每一个主成分为一个点,通过“坡度趋于平缓”的未知判断提取主成分的数量。
4、因子载荷系数表
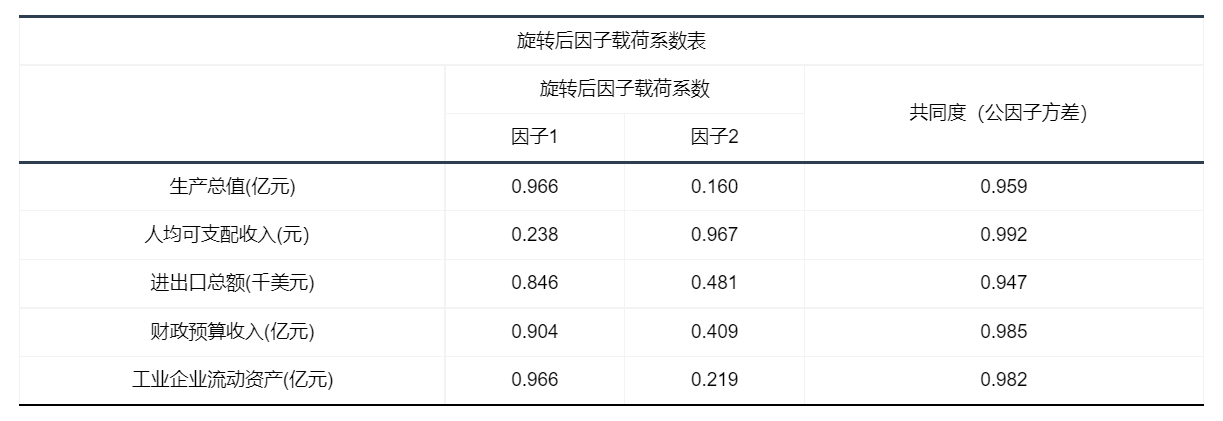
图表说明: 上表为因子载荷系数表,可以分析到每个主成分中隐变量的重要性。
● 假设前文确定得到n个因子,因子i中a,b,c,d的因子载荷系数较大,因此可将因子i确定为某一个成分(可进行总结重命名)。
5、成分矩阵表
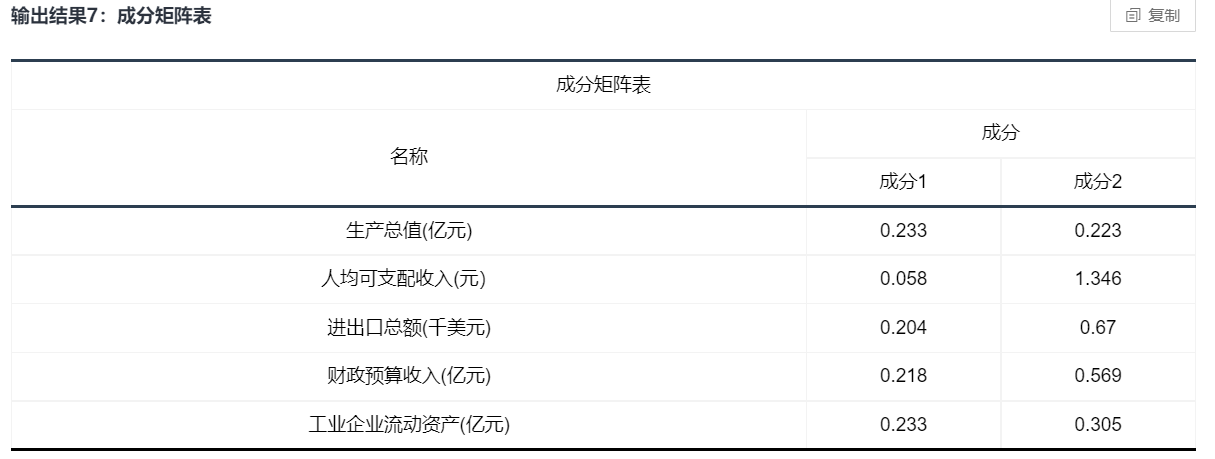
图表说明: 上表为成份矩阵表,意在说明各个成分的所包含的因子得分系数(主成分载荷),用于计算出成分得分,得出主成分公式。
智能分析:模型的公式: F1=0.233×生产总值(亿元)+0.058×人均可支配收入(元)+0.204×进出口总额(千美元)+0.218×财政预算收入(亿元)+0.233×工业企业流动资产(亿元) F2=0.223×生产总值(亿元)+1.346×人均可支配收入(元)+0.67×进出口总额(千美元)+0.569×财政预算收入(亿元)+0.305×工业企业流动资产(亿元) 由上可以得到: F=(0.691/0.973)×F1+(0.282/0.973)×F2
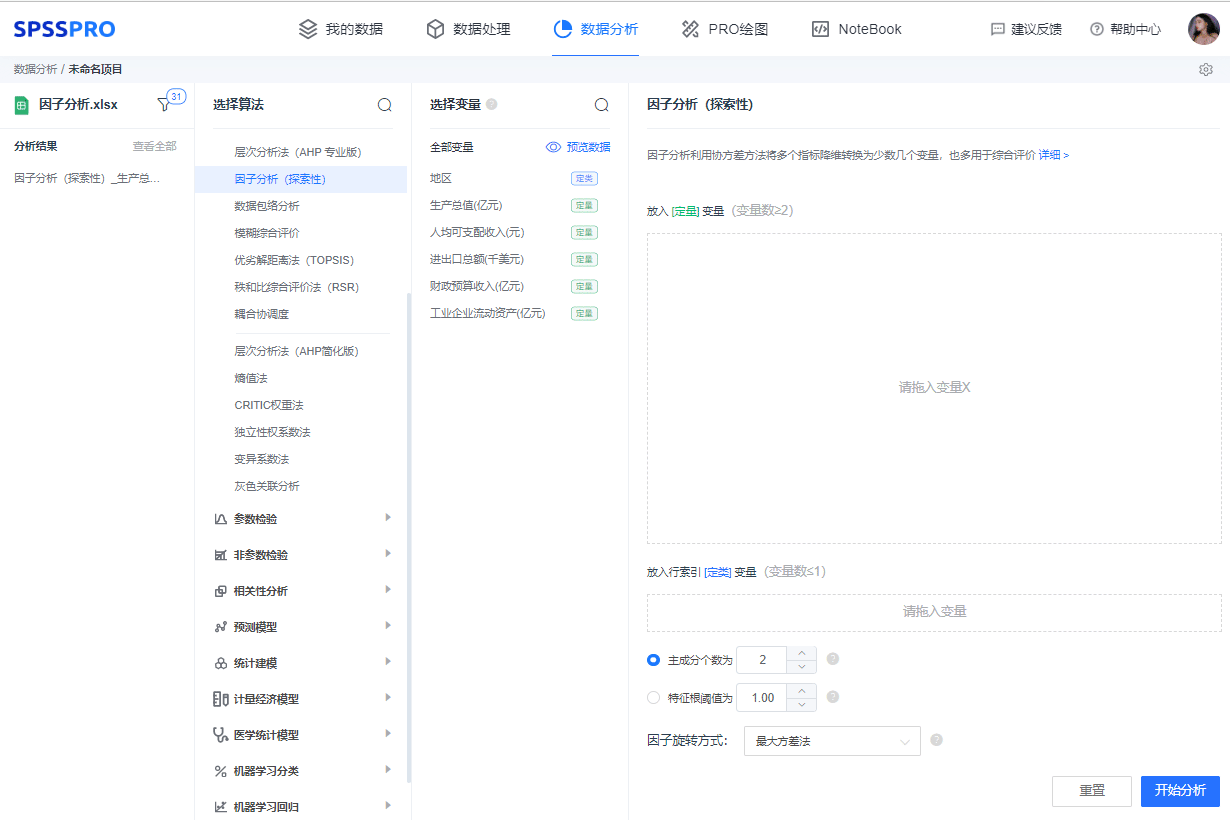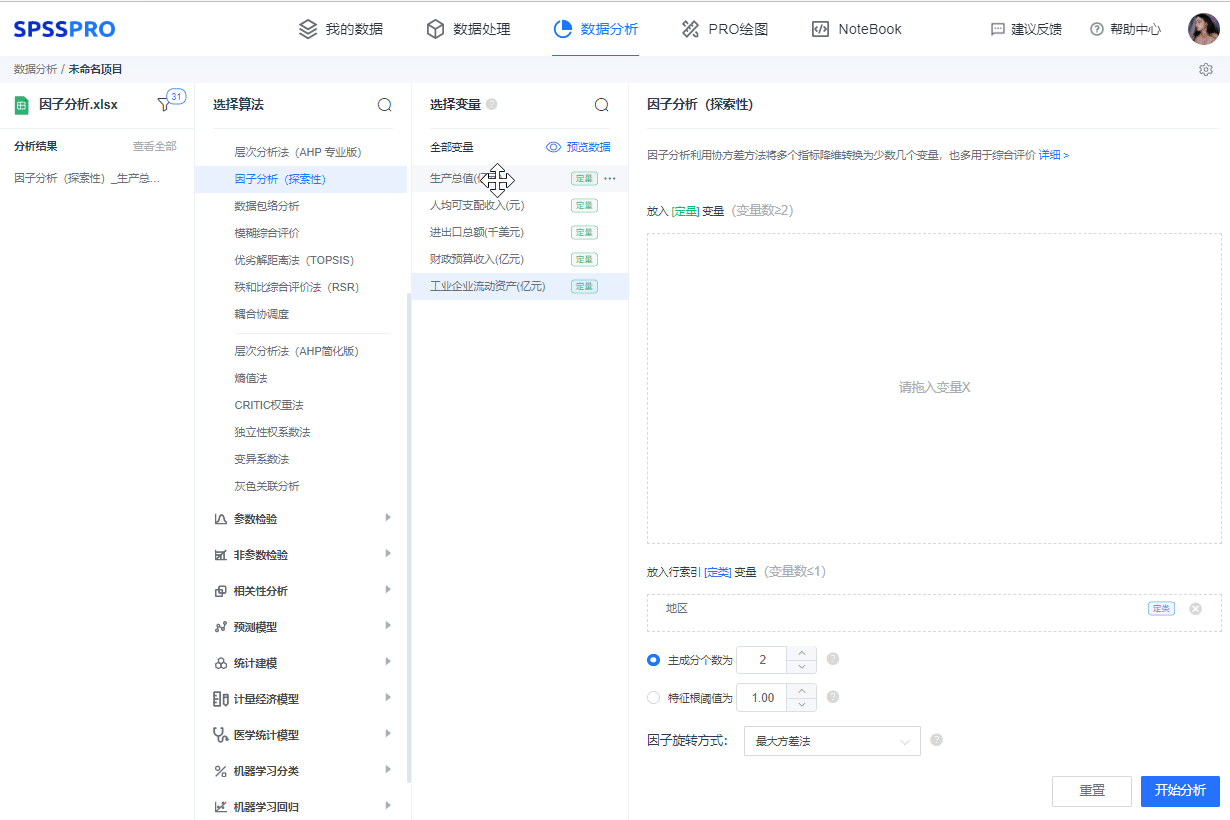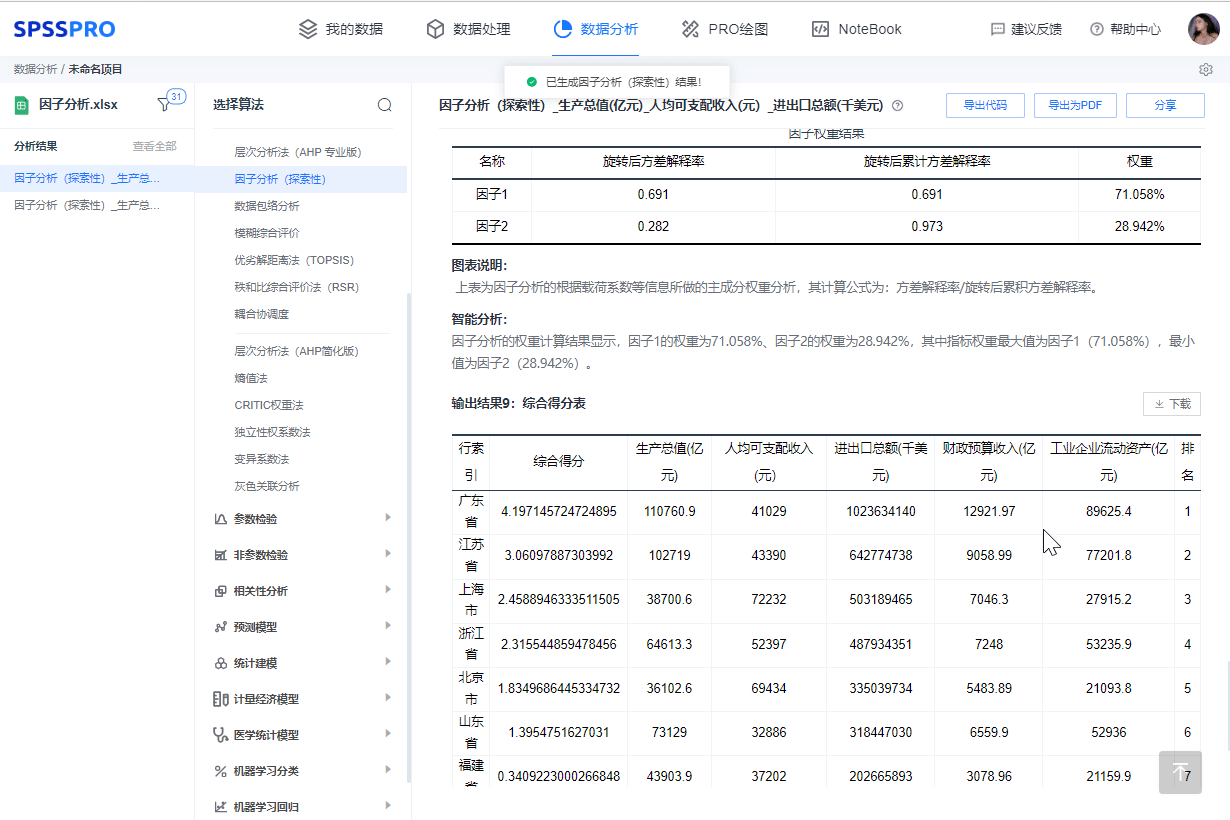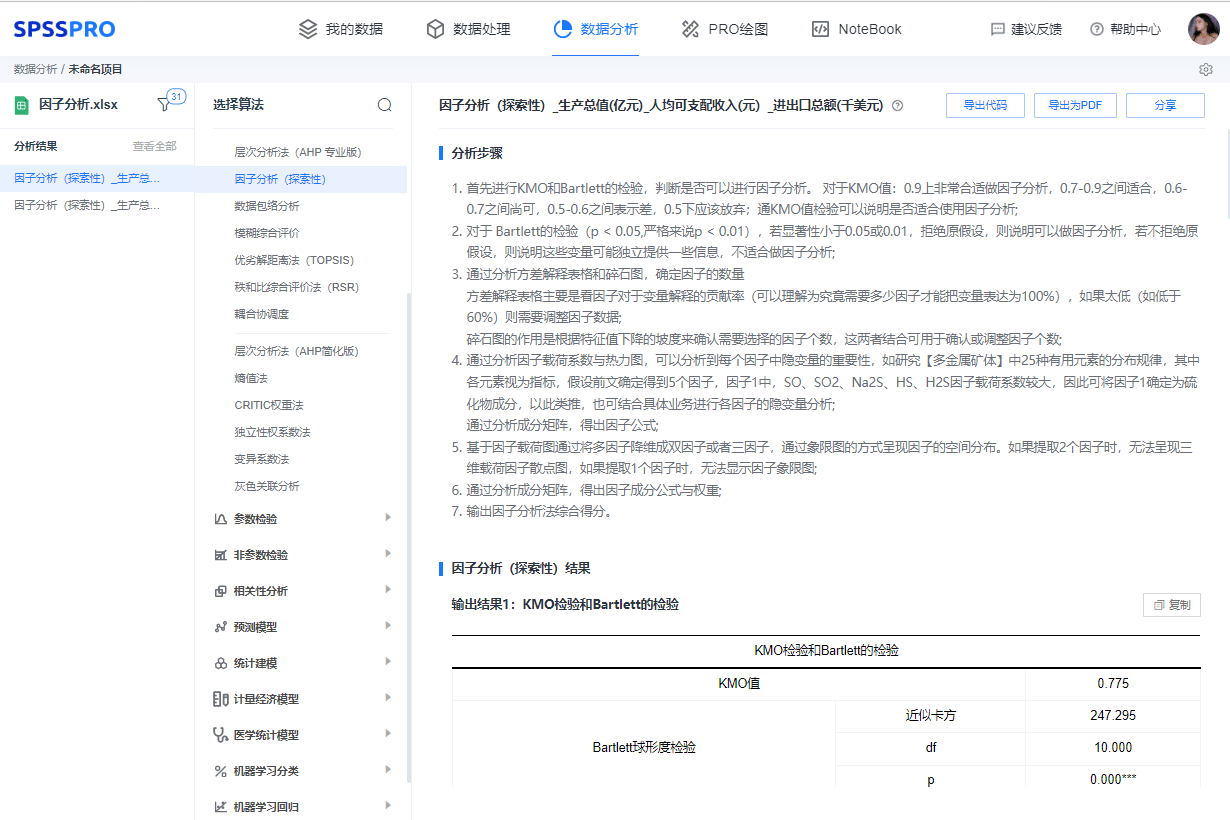
6、因子权重分析

图表说明: 上表为因子分析的根据载荷系数等信息所做的主成分权重分析,其计算公式为:方差解释率/旋转后累积方差解释率。
智能分析:因子分析的权重计算结果显示,因子1的权重为71.058%、因子2的权重为28.942%,其中指标权重最大值为因子1(71.058%),最小值为因子2(28.942%)。

发表评论