作品编号：022

《勾股定理（第一课时）》是人教版教材八年级下册第十七章的第一节课内容，是在学生已经掌握了三角形甚至直角三角形的一些知识之后，对直角三角形的三边做进一步研究，主要验证“直角三角形两条直角边的平方和等于斜边的平方”，教材从毕达哥拉斯的发现，通过猜想、切割、拼接、计算等数学活动，探究勾股定理的原由．本文在不改变教材设计意图的基础上，学生通过分割、拼接、类比、归纳、数形结合、演绎推理等多种数学思想方法，体验勾股定理的不同证法，展示勾股定理由来的严谨性，有效培养学生创新性思维和发散性思维，同时将有关勾股定理数学史材料适时地引进课堂，使勾股定理的教学成为一个数学文化贯穿于课堂的新形式．

一、了解勾股定理的起源和发现

老师介绍：（地砖里的秘密）在2500多年前，古希腊著名的哲学家、天文学家、数学家毕达哥拉斯有一次在朋友家做客时，发现朋友家用地砖铺成的地面图案反映了等腰直角三角形三边的某种数量关系．

问题：如图1，现在就让我们一同回到2500年前，体验一下毕达哥拉斯的经历，地砖中隐含着直角三角形三边数量关系是什么？

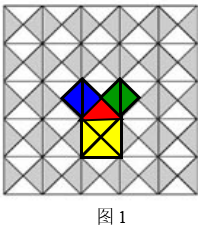
追问：地砖是由全等的等腰直角三角形拼接而成的，每个等腰直角三角形都相邻3个正方形，这3个正方形面积间有怎样的数量关系？你是怎样得出来的？

师生活动：在问题的引领下，学生逐渐发现等腰直角三角形的直角边为边长的小正方形是由2个等腰直角三角形组成的，以斜边为边长的大正方形是由4个等腰直角三角形组成的，可见两个小正方形的面积之和等于大正方形的面积；而每个正方形的面积都可以用边长的平方表示，所以等腰直角三角形两直角边（a 和b，此时a =b）的平方和等于斜边（c）的平方，即，这样就得到等腰直角三角形三边的数量关系．

设计意图：通过历史故事引入，了解勾股定理起源的文化背景，同时将面积关系转化为等腰直角三角形三边的数量关系，使学生明白 ，，的几何意义，体验“面积法” 证明几何中的数量关系，为探索一般直角三角形三边关系提供了方向和线索；这种通过特殊实例猜想一般结论，再加以论证，也是我们平常提倡的科学探索之法．

二、探究勾股定理的证明

1.借鉴面积分割，还原欧几里得证法

问题：等腰直角三角形满足上述关系，是不是所有的直角三角形都有这个性质呢？

追问：对于这个猜想，我们是否可以借鉴以上的思路，探究两个小正方形的面积之和是否等于大正方形的面积呢？

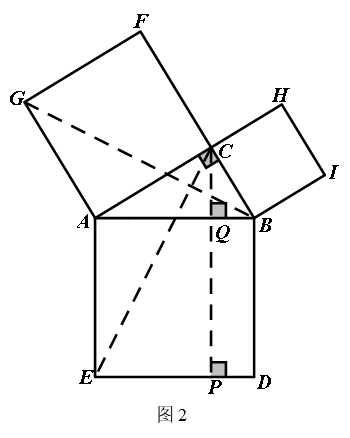
师生活动：在教师适时引导下，师生共同完成，设△ABC为一直角三角形，其中C为直角顶点，在各边上向外作正方形ABDE、正方形BCHI和ACFG，作CQ⊥DE于P，与AB交于Q， 分别连接CE、BG，得△ACE，△AGB；因为AE＝AB，AC＝AG ，∠CAG+∠CAB＝∠BAE+∠CAB， 即∠CAE=∠GAB，可证△ACE≌△AGB，得．

∵，，

∴=．

同理=

∴=．

同理，=．

∴+=+．

∴+=，即．

教师介绍：可见，对于一般的直角三角形，也可以通过两个小正方形的面积之和等于大正方形的面积，得出直角三角形三边的数量关系，其实这还原了欧几里得《几何原本》中所载的勾股定理的证法，在西方文献中，它是最早证明勾股定理的文字记载．这本著作以人们公认的一些事实作为定义和公理，再通过演绎推理得到了更多的定理和结论；欧几里得（公元前330年—公元前275年），古希腊人，数学家．

设计意图：这种方法虽然不简单，需要老师适时引导和讲解，但是它向学生展示勾股定理的证明不仅只有教材中介绍的拼图来验证，还可以运用面积分割法和几何演绎推理．

2.借助拼接图形，领略传说中的毕达哥拉斯证法

老师介绍：毕达哥拉斯虽然运用两小正方形的面积之和等于大正方形的面积，来验证等腰直角三角形两直角边的平方和等于斜边的平方，但对于一般的直角三角形，相传他是结合拼接图形来完成证明的，现在我们一起来领略毕达哥拉斯证法．

问题：请把8个以a，b为直角边， c 为斜边的全等直角三角形和3个边长分别为a，b，c的正方形拼成两个边长都是a+b的正方形．

师生活动：在师生一起努力下，拼出图3和图4，显然图3和图4的四边形ABCD均为正方形．

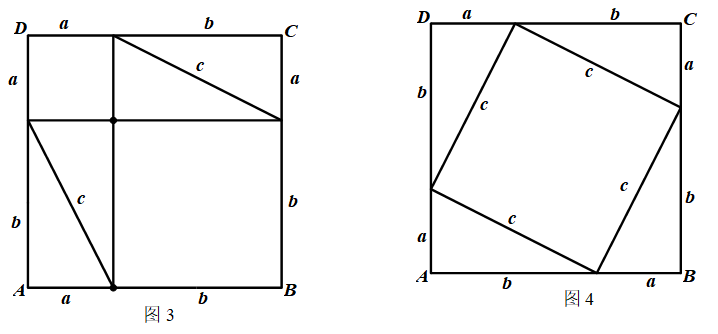
根据两个正方形ABCD面积相等，得， 整理得．

老师介绍：以上就是“拼图法”证明勾股定理的经典例子，主要是利用两正方形的面积相等列出等式，而每一个正方形看成是不同小图形的面积之和，最终证明勾股定理的成立．毕达哥拉斯是世界上第一个给出直角三角形三边关系的人，所以许多西方国家称该结论为毕达哥拉斯定理，对于毕达哥拉斯是如何证明勾股定理，并没有确切的史料记载，所以这种证明方法仅仅相传是毕达哥拉斯证法．

设计意图：这种方法是先将图形进行拼接，然后运用图形面积关系来证明定理，是为后续证法起铺垫作用，通过拼图和对定理的论证，锻炼学生的动手实践能力，巩固了一些基本图形的面积计算方法．

3.减少拼图数量，欣赏邹元治证法

老师介绍：用毕达哥拉斯证法过程中，同学们发现可以减少拼接的图形．

问题：根据同学们的反馈，只需4个以a，b 为直角边， c为斜边的全等的直角三角形，就可以拼成一个边长为a + b的正方形，怎么拼接？如何证明？

师生活动：把这4个以a，b 为直角边， c为斜边的全等的直角三角形，拼成图5所示的图形，使A，E，B三点在一条直线上，B，F，C三点在一条直线上，C，G，D三点在一条直线上．

证明：∵ RtΔAHE ≌ RtΔBEF，

∴ ∠1 = ∠3．

∵ ∠1 + ∠2 = 90º,

∴ ∠3 + ∠2 = 90º．

∴ ∠HEF = 90º．

同理，∠ EFG=∠FGH=90º．

∴∠EHG = 90º，且四边形EFGH是一个边长为c的正方形，它的面积等于．

∵ RtΔDHG ≌ RtΔAEH，

∴ ∠4 = ∠1．

∵ ∠4 + ∠5 = 90º，

∴ ∠1 + ∠5 = 90º．

∴ ∠DHA =∠EHG+∠1 + ∠5= 180º．

∴D，H，A三点在一条直线上．

∴四边形ABCD是正方形．

∴．

∴．

老师介绍：这种证法是我国近代数学家邹元治所采用的方法，在国内常常被提及，和西方数学史家所推测的毕达哥拉斯的证明方法有相似之处，不过毕达哥拉斯只是利用拼图直观地推出定理结论，邹元治简化拼图过程，并给予了严格的演绎证明．

设计意图：这种验证勾股定理的方式减少了拼图，易于拼接，用形数结合的方法，给出了勾股定理的详细推理论证，又是我国的数学家给出的证明，这样也可以增加学生的民族自豪感．

4.转化拼图方式，体验赵爽证法

问题：转变拼图方法，仅用4个全等的直角三角形能否拼成一个边长为c的正方形？

师生活动：如图6，以a，b ( a

证明：∵ RtΔDAH ≌ RtΔABE，

∴ ∠ADH= ∠BAE．

∵ ∠ADH + ∠DAH = 90º，

∴ ∠BAE + ∠DAH = 90º，即∠BAD= 90º．

同理，∠ABC =∠BCD=∠CDA= 90º．

∴ 四边形ABCD是一个边长为c的正方形，它的面积等于．

∵ EF = FG =GH =HE = b-a ，∠HEF =∠EFG=∠FGH=∠GHE= 90º．

∴四边形EFGH是一个边长为b-a的正方形，它的面积等于．

∵．

∴．

老师介绍：这种证法类似于我国三国时期的数学家赵爽为《周髀算经》作注解时给出的证明方法，赵爽是我国历史上杰出的数学家，他也对图形进行切割和拼接，巧妙地利用面积关系证明了勾股定理，该图称为“赵爽弦图”，被选为2002年在北京召开的国际数学家大会的会徽．我国也是发现并研究勾股定理最古老的国家之一，古代数学家把两条直角边称为勾（短边）和股（长边），斜边称为弦，这就是我国称之为勾股定理的由来．

设计意图：赵爽和邹元治都是利用几何图形的拼接和面积关系来证明代数式之间的恒等关系，既具有直观性，又具有严密性，为学生展示了数形统一、以形证数的经典方法；同时介绍我国古代数学家对勾股定理的研究成果，培养学生爱国热情和民族荣誉感．

5.再次减少拼图，介绍总统证法

问题：在图5基础上，连接FH，如图7，把图形分割成两个全等的直角梯形，取其中一个直角梯形，是否可以推导出勾股定理？

师生活动：也可以这样做，以a，b 为直角边，c为斜边的2个全等的直角三角形，拼成一个如图8所示的梯形，使A，E，B三点在一条直线上．

证明：由A，E，B三点在一条直线上，易得AH//BF，∠HEF=．

∴．

∴．

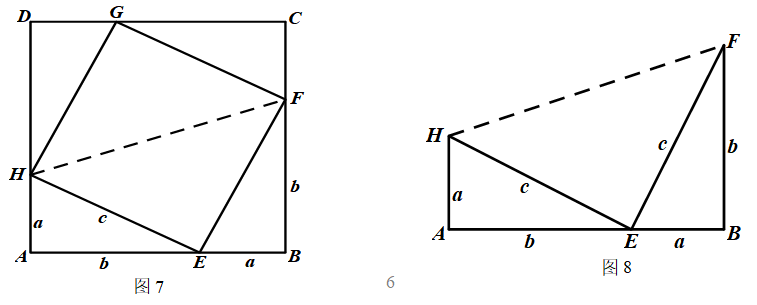
老师介绍：这是美国第20任总统加菲尔德构造的图形，他不是数学家，他却给出了一种非常经典的证法，后人称之为勾股定理的总统证法．从古至今，许多数学研究者或数学家对勾股定理的证明孜孜不倦，各种证法不一而足，据统计，已有不同证法500多种，这几百种证法中，有的十分精巧，有的十分简明，有的因为证明者身份的特殊而闻名．

设计意图：总统证法简洁明快，证明中所用的图形是以往图形的部分，构成新的证法，让学生体会各种证法之间的演变与继承，有利于找出它们之间的区别和联系，培养学生归纳总结能力和发散思维．

勾股定理证法众多，教学方式精彩纷呈，本节课的教学设计注重知识的生成和发展，适时穿插着文化背景，选取5种来自不同国家、不同时期、不同方法的证明思路，较为自然地经历并体验勾股定理的重新发现及证明，为学生获取知识的同时提升数学文化素养．

参考文献

[1]曲晓芹．人类智慧之光 ——勾股定理[J] ．中小学数学·初中版，2008（7-8）．

[2]马梦阳．勾股定理的证明及推广应用[D] ．西安：西北大学，2014．

[3]杨勤春．中学数学教学应重视数学文化教育[J] ．福建基础教育研究，2010（2）．

已发文章>>