如果说解析几何是高中数学教学的重点内容之一,那么核心部分就是圆锥曲线。圆锥曲线综合问题一般被高考命题老师用来考查考生的分析处理信息的能力、划归与转化能力、数形结合做题能力、解题计算能力等,同时检验学生对基础知识的掌握情况与灵活运用能力。因此跟圆锥曲线有关的内容是每年高考的必考内容之一,如直线与圆锥曲线是高考数学重点考查内容。

纵观近几年全国各地的高考数学题,我们发现与圆锥曲线相关的综合问题的分值在试卷中所占比例有明显的增加趋势,题目的形式也比较新颖。圆锥曲线综合问题常涉及点和直线与圆锥曲线的位置关系、方程与函数不等式等重要的数学知识。

今天我们就一起来讲讲高考数学热点考点：圆锥曲线综合问题。

研究直线与圆锥曲线的位置关系时，一般转化为研究其直线方程与圆锥方程组成的方程组解的个数，但对于选择、填空题也可以利用几何条件，用数形结合的方法求解。

直线与圆锥曲线的位置关系，主要涉及弦长、弦中点、对称、参数的取值范围、求曲线方程等问题。解题中要充分重视根与系数的关系和判别式的应用。

当直线与圆锥曲线相交时：涉及弦长问题，常用“根与系数的关系”设而不求计算弦长(即应用弦长公式)；涉及弦的中点问题，常用“点差法”设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化。同时还应充分挖掘题目中的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍。解题的主要规律可以概括为“联立方程求交点，韦达定理求弦长，根的分布找范围，曲线定义不能忘”。

典型例题1：

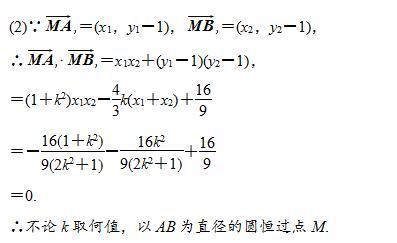
直线与圆锥曲线的位置关系

判定直线与圆锥曲线的位置关系时，通常是将直线方程与曲线方程联立，消去变量y(或x)得关于变量x(或y)的方程：ax2＋bx＋c＝0(或ay2＋by＋c＝0)。

若a≠0，可考虑一元二次方程的判别式Δ，有：

Δ>0⇔直线与圆锥曲线相交；

Δ＝0⇔直线与圆锥曲线相切；

Δ

若a＝0且b≠0，则直线与圆锥曲线相交，且有一个交点。

圆锥曲线上两点关于直线对称问题一直是高考数学试题中的"常青树",

高考数学既注重对数学基础知识的全面考查,又注重对数学思想和思维方法的考查,特别强调利用数学知识和数学思想处理实际问题能力的考查。圆锥曲线综合问题具有综合性强、题目新颖、灵活多样,对解题能力要求比较高,自然就成为高考数学的热点，但这也给考生带来一定的难度,。

典型例题2：

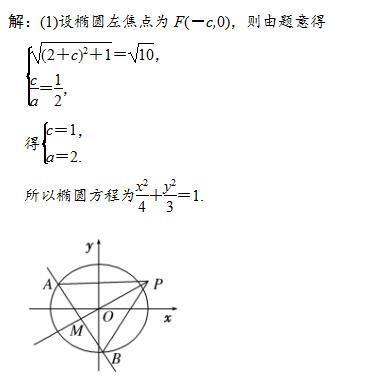
解决圆锥曲线的最值与范围问题常见的解法有两种：几何法和代数法。

1、若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决，这就是几何法；

2、若题目的条件和结论能体现一种明确的函数关系，则可首先建立起目标函数，再求这个函数的最值，这就是代数法。

在利用代数法解决最值与范围问题时常从以下五个方面考虑：

1、利用判别式来构造不等关系，从而确定参数的取值范围；

2、利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；

3、利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；

4、利用基本不等式求出参数的取值范围；

5、利用函数的值域的求法，确定参数的取值范围。