文：浣熊老师

这是佛法数学的第6篇。

「图解数学」系列介绍

「图解数学」系列用学生看起来最为直观的图形，载12期，来讲解SAT/ACT/AMC8平面几何的考点，并提供中英文对照。

本期要点：

1.直角三角形三边长关系

2.勾股定理的历史

3.勾股数

4.一般三角形三边长关系

日常生活中，用到最多的三角形非直角三角形莫属了——桌子、墙壁、书本都是直角的。

一个直角三角形有两个直角边（two legs）和一个斜边（hypotenuse）。它们之间的关系是什么样的呢？请观察下图：

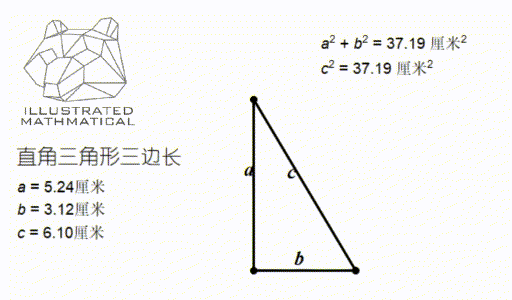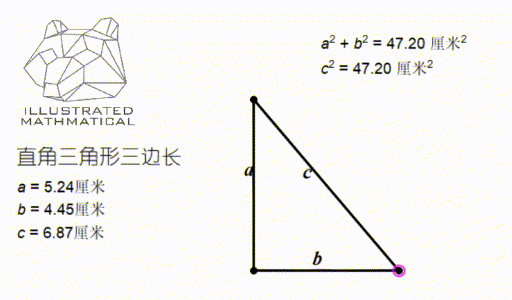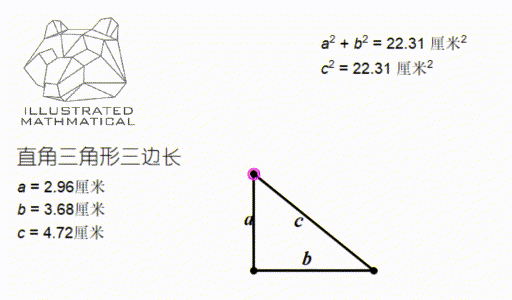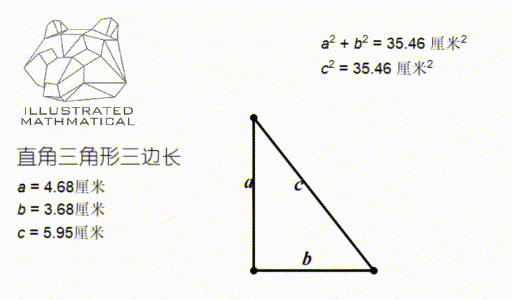
看图我们可以发现，无论这个三角形是胖的瘦的、高的矮的怎么变化，我分别测量三边的值 a，b，c，它们之间都满足一个关系式：

这就是著名的勾股定理了。

勾股定理为什么叫这个名字，“勾”和“股”的意思是什么？为什么在国外它会被称为Pythagorean Theorem，我们来看看它的由来：

中国古人把直角三角形较小的直角边叫做勾，较长的直角边叫做股，斜边叫做弦，描述三者关系的定理就叫勾股定理。早在春秋时期，它就被中国人发现，后记载于《九章算数》。

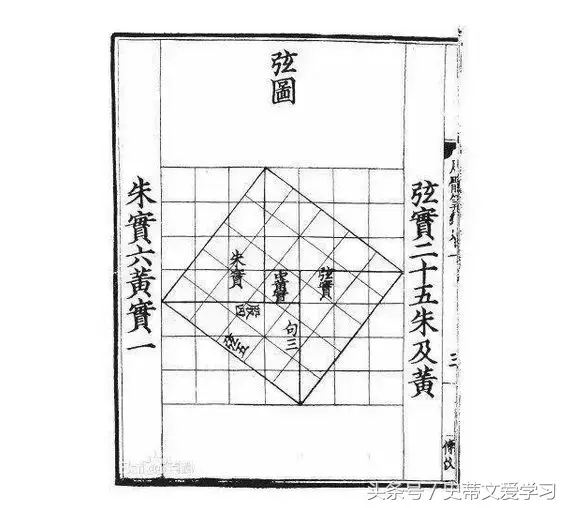
客观的说，虽然中国人早于西方发现这一性质，但最先将此性质推广到任意直角三角形并予以证明的是古希腊数学家毕达哥拉斯 (Pythagoras) ，因此这个定理也叫做毕达哥拉斯定理 (Pythagorean Theorem) ，我们常见到的黄金分割、整数、分数这些概念也源于毕达哥拉斯学派。

在前面的例子中，我们知道如果一个三角形是直角三角形，那么它的三边 (a,b,c) 就满足 a 方加 b 方等于 c 方。

而在实际题目中，三边长经常以整数的形式出现，如 （3,4,5）/（6,8,10）/（5,12,13）

这样的 (a,b,c)既满足勾股定理，又是整数的三个数为一组，就叫“勾股数”（pythagorean triple) ,勾股数有两个基本性质。

一：所有勾股数可以不重不露的表示出，低年级掌握四个即可。

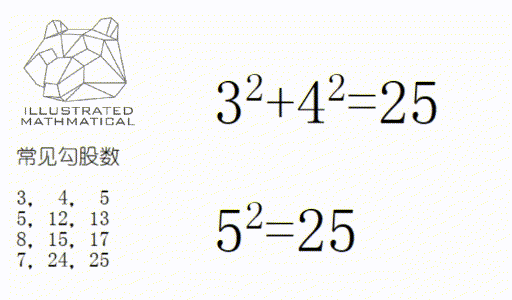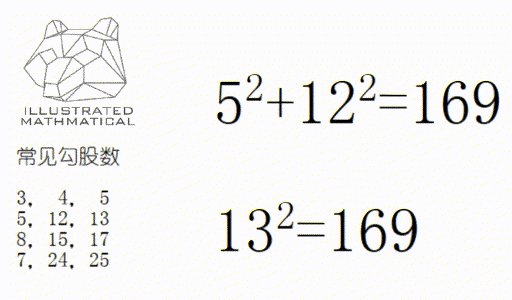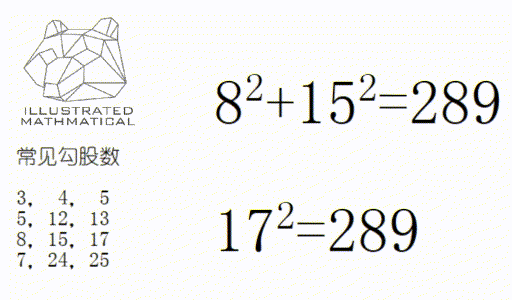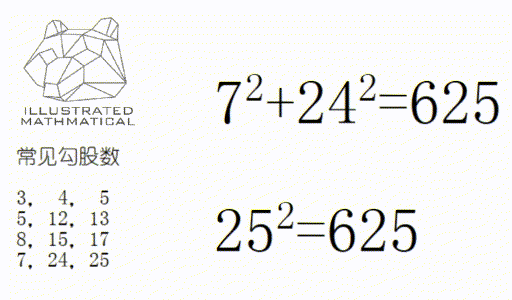
二：如果一组数是勾股数，那么它们的倍数依然是勾股数。

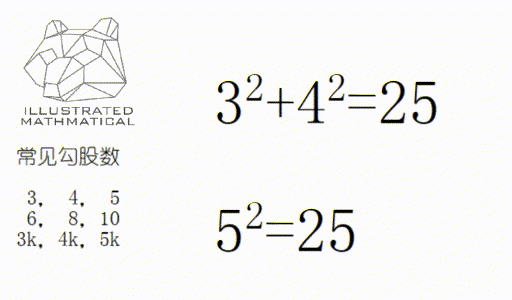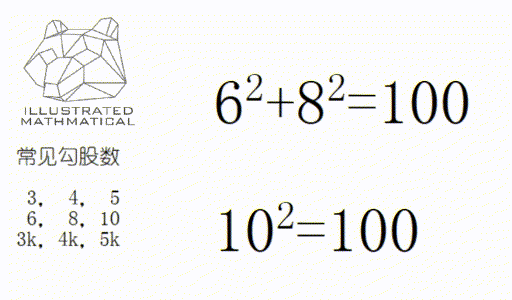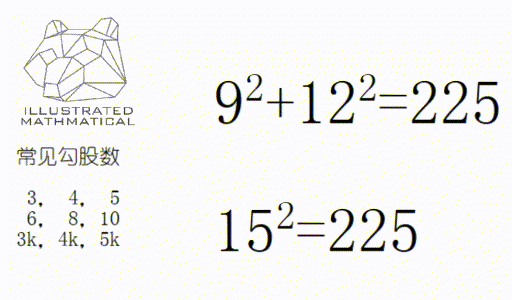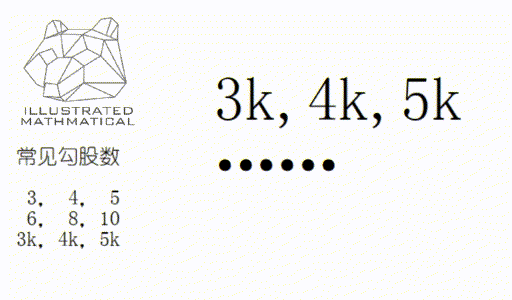
用以上两条技巧，很多题就能快速口算出来！

如果一个三角形不是直角三角形，而是钝角或者锐角，三边长关系又是怎么样呢？

如果想精确到具体数字计算，需要高中的正弦定理（sine rule）和余弦定理（cosine rule），但是，我想说的是：其实不用它们，我们用初中的方法已经可以定性的估计了。

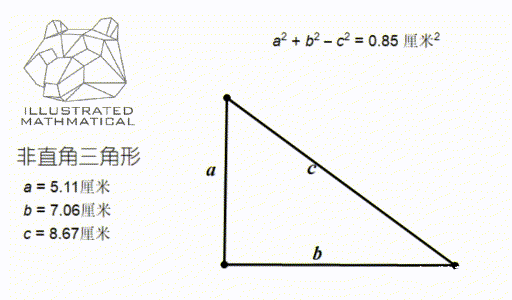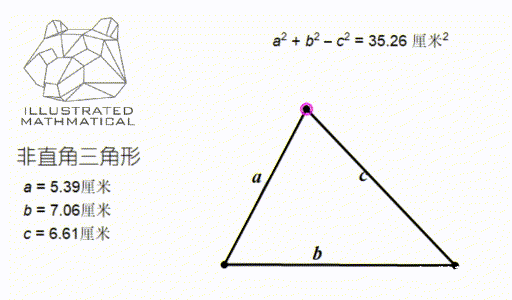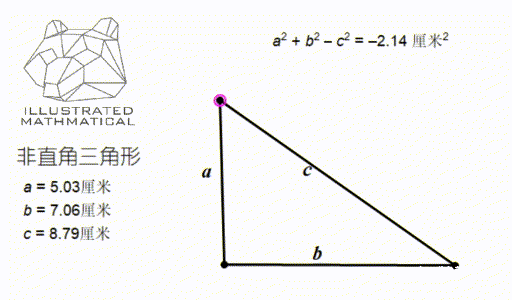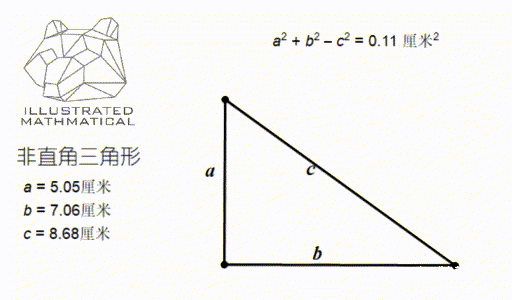
仔细观察上图发现，当这个角是锐角时， a 方加 b 方减 c 方的值是正数，即 a 方加 b 方 大于 c 方；如果夹角是钝角时则正好相反。

也就说明：只有这个三角形是直角三角形，才会有 a 方加 b 方 刚好等于 c 方。

用这个性质，可以推导出勾股定理逆定理：如果一个三角形两边的平方和等于第三条边的平方，那么这个三角形是直角三角形。

今天你学习了《图解数学》的第六讲，了解勾股定理和直角三角形。恭喜你，又解锁了一个新章节。下次我们学习平行四边形。