波动率决定了资产收益中不可预测部分的行为。设资产收益为条件正态分布,且均值和方差时变,则:
f(r_t | \Omega_{t-1} )= N(\mu_t , \sigma_t^2)
考虑AR(1)模型:
r_t = \phi_0 + \phi_1 r_{t-1} + a_t
其条件均值为 \mu_t = \phi_ 0 +\phi_1 r_{t-1} 。
定义条件方差为:
\sigma_t^2 = E[(r_t - \mu_t )^2 | \Omega _{t-1}] = E(a_t^2 | \Omega_{t-1})
由于方差是时变的,因此允许它随时间 t-1 的信息变化而变化。如果市场几乎是有效的,那么回报是不可预测的。如果条件均值非常小,则条件方差可以表达为:
\sigma^2_t = E[(r_t - \mu_t)^2 | \Omega _ {t-1}] = E(r_t^2 | \Omega_{t-1})
因此,多日方差是单日方差的总和。如果一年中每天的方差都是一样的,那么年化方差就是总天数乘以每日方差。
条件异方差
条件异方差的典型事实:
波动率建模
历史波动率为:
\displaystyle \sigma = \sqrt {252 \sum_{j=T-K}^T \frac{r_j^2}{K}}
选择大 K ,这样估计更准确。
指数平滑为:
\displaystyle \sigma_t ^2 = \lambda \sigma_{t-1}^2 + (1-\lambda ) r_{t-1}^2
以上模型的波动率都是时变的。
波动性模型可以分为两大类:
用精确的函数来控制方差的演化(如ARCH/GARCH)用随机方程来描述资产方差(如随机波动率模型)
建立资产收益序列的波动率模型包括四个步骤:
检验数据中的序列依赖性,指定一个均值方程,为回归序列建立一个计量模型以消除线性依赖性用均值方程的残差来检验ARCH效应如果ARCH效应在统计上显著,则指定波动率模型,并对均值和波动率方程进行联合估计检查拟合模型并进行改进ARCH效应
设 a_t 为均值方程的残差,有 a_t = r_t - \mu _t 。残差平方 a_t^2 用于检查条件异方差,也被称为ARCH效应。有两种检验可用:
(1)Ljung-Box的Q检验,对于 a_t^2序列(细节见前一章)
(2)恩格尔(Engle)的拉格朗日乘数检验,等价于一般的F检验:
跑一个辅助线性模型(auxciliary linear model):
a_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \cdots + \alpha_m a_{t-m}^2 + e_t
原假设为 \alpha_1 = \cdots =\alpha_m = 0 。定义:
\displaystyle SSR_0 = \sum_{t=m+1}^T (a_t^2 - \bar a)^2 , \displaystyle \bar a = \frac{1}{T}\sum_{t=1}^T a_t^2
以及:
\displaystyle SSR_1 = \sum_{t=m+1}^T \hat e_t^2
F统计量为:
\displaystyle F = \frac{(SSR_0 - SSR_1)/m }{SSR_1 / (T-2m-1)} , mF \sim \chi^2 (m) ARCH模型
自回归条件异方差模型(ARCH),其含义拆解为:
ARCH的关键思想是:
ARCH(p)模型为:
现在讨论ARCH模型的性质。ARCH(1)模型为:
其中 h_t 为条件方差。
r_t 的无条件均值为 \mu
r_t 的无条件方差为:
Var(r_t) = E(a_t^2) = E(E(h_t|\Omega_{t-1}))=E(\alpha_0 + \alpha_1 a_{t-1}^2) = \alpha_0 + \alpha_1 E(a_{t-1}^2)
得:
\displaystyle Var(r_t) = \frac{\alpha_0}{1-\alpha_1}
偏度为0。
四阶矩为:
\displaystyle E((r_t-\mu)^4) = \frac{3\alpha_0^2 (1+\alpha_1)}{(1-\alpha_1)(1-3\alpha_1^2)}
峰度为:
3">\displaystyle K= \frac{E((r_t-\mu)^4) }{(Var(r_t))^2} = 3 \frac{1-\alpha_1^2}{1-3\alpha_1^2} > 3
ARCH模型的缺陷有:
GARCH模型
广义自回归条件异方差模型(GARCH)是ARCH模型最重要的扩展。GARCH(p,q)模型为:
\displaystyle \sigma_t^2 = \alpha_0 + \sum_{i=1}^p \alpha_i a_{t-i}^2 + \sum_{j=1}^q \beta_j \sigma_{t-j}^2
明天的方差被预测为长期均值方差、今天的方差预测、冲击(今天的误差平方)的加权平均。GARCH是一个非常成功和有弹性的经验模型,因为与ARCH相比,它的参数较少,可以更简洁地表示波动性聚类。GARCH(1,1)相当于ARCH(∞)。ARCH(p)是一个简单的GARCH(p,0)模型,其中在过去的条件方差预测过程中没有记忆。最简单但非常强大的模型是GARCH(1,1):
其中, e_t = (r_t - \mu) / (h_t^{1/2}) \sim N(0,1) ,令 a_t = h_t ^{1/2} e_t ,GARCH(1,1)也可以写为:
第二行 a_{t-1} = h_{t-1} ^{1/2} e_{t-1} ,代入并整理得到:
h_t = \alpha_0 + (\alpha_1 e_{t-1}^2 + \beta_1) h_{t-1}
两端取期望,化简得:
E(h_t) = \alpha_0 + (\alpha_1 + \beta_1) E(h_{t-1})
进而得到:
\displaystyle \sigma^2 = \frac{\alpha_0}{1-(\alpha_1 + \beta_1)}
该序列弱平稳(协方差平稳)当且仅当 \alpha_1 + \beta_1 < 1 。
波动率过程也可以写为:
h_t = (1-(\alpha_1 + \beta_1))\sigma^2 + \alpha_1 a_{t-1}^2 + \beta_1 h_{t-1}
是无条件方差、昨日方差预测、昨日冲击或新闻的加权平均值。
回报率的无条件均值和方差分别为:
无条件三阶矩为:
E((r_t-\mu)^3) = E(h_t ^{3/2})E(e_t ^3) = 0
回报率的峰度 K 为:
E((r_t-\mu)^4) = E(h_t ^{2})E(e_t ^4) =3 E(h_t^2) ;
\displaystyle K = \frac{3E(h_t^2)}{\sigma^4} = 3 \frac{1-(\alpha_1 + \beta_1)}{1-2 \alpha_1 ^2 - (\alpha_1 + \beta_1 )^2}
当 2 \alpha_1 ^2 + (\alpha_1 + \beta_1 )^2 时,峰度大于3。
GARCH的特点可以总结为:
2. 模型探究模型估计
GARCH模型不是通常的线性形式,不能用OLS。需要使用极大似然估计(MLE),查找给定数据的参数的最可能值,即形成一个对数似然函数并使其最大化。
考虑一个具有同方差误差的简单回归:
y_t = \alpha+ \beta x_t + a_t
正态分布随机变量的概率密度函数为:
\displaystyle f(y_t | \alpha + \beta x_t, \sigma^2) = \frac{1}{\sigma \sqrt {2 \pi}} \exp \left[ -\frac{1}{2} \frac{(y_t - \alpha - \beta x_t )^2}{\sigma^2 } \right]
若 a_t 独立同分布,则 y_t 也独立同分布。所有 y_t 的联合分布可以表示为单个密度函数的乘积:
\displaystyle f(y_1,...,y_t | \alpha+\beta x_t , \sigma^2) = \prod_{t-1}^{T} f(y_t | \alpha+\beta x_t , \sigma^2)
得到:
\displaystyle f(y_1,...,y_t | \alpha+\beta x_t , \sigma^2) = \frac{1}{\sigma^T (\sqrt {2 \pi})^T} \exp \left[ -\frac{1}{2} \sum_{t=1}^T\frac{(y_t - \alpha - \beta x_t )^2}{\sigma^2 } \right]
上面的方程是似然函数,可以写成 LF(\alpha,\beta,\sigma^2) 。最大似然函数就是找出使似然函数最大化的这些变量的值。对这些参数最大化乘法函数是复杂的,因此取其对数来获得对数似然函数(LLF):
\displaystyle LLF = -T \log (\sigma) - \frac{T}{2} \log (2\pi) - \frac{1}{2} \sum_{t=1}^T \frac{(y_t -\alpha -\beta x_t )^2}{\sigma^2 }
上式中的第一项可以替换为 -(T/2) \log (\sigma^2) 。用一阶条件对每个参数求解该函数,得到与OLS相同的估计量,最大似然方差一致但有偏。对于GARCH模型,方差是时变的,因此需要将 -(T/2) \log (\sigma^2) 替换为:
\displaystyle -\frac12 \sum_{t=1}^T \log (\sigma_t^2)
也将 \sigma^2 替换为 \sigma^2_t 。一般不能用解析法达到最优化,而是使用数值法:
设定对数似然函数使用回归得到平均参数的初始猜测为条件方差参数选择一些初始猜测指定一个收敛准则:按准则或按值
如果误差确实是正态的,这种估计对于大样本是最优的。如果没有正态性,可以用拟极大似然估计(Quasi-MLE)。本质上,对于极大似然估计,所有数值方法都是通过在参数空间上搜索,直到找到使对数似然函数最大化的参数值。
给定参数估计的一组初始猜测,这些参数值在每次迭代中更新,直到程序确定已研究出最优。如果对数似然函数对于参数值只有一个最大值,那么任何优化方法都应该能够找到它,但运行时间可能有差异。然而,就像GARCH等非线性模型的情况一样,对数似然函数可以有很多局部极大值。最大似然方法在估计GARCH模型参数时,似然面中的局部最优或多模态存在潜在的严重缺陷。
GARCH(1,1)模型中,三个参数都应该是正的。为了确保波动过程是平稳的, \alpha+\beta 。非常接近于1表明波动性非常持久。估计的无条件方差应该接近数据方差。
模型检验
检验非线性限制,或检验非线性模型的假设。有三种经典的检验,考虑不同的问题:
LR检验需要对受限模型和非受限模型进行估计。LR统计量为:
LR = -2 (L_r-L_u) \sim \chi ^2 (k)
LM检验只需要对受限模型进行估计,它涉及对数似然函数相对于受限估计处的参数的一阶和二阶导数。
沃尔德检验只涉及估计无限制回归,通常OLS的t检验和F检验都是沃尔德检验的例子。
这三个检验都假定估计量的正态性,检验统计量渐近为 \chi^2 。它们是渐近等价的。
可以用图象直观观察:
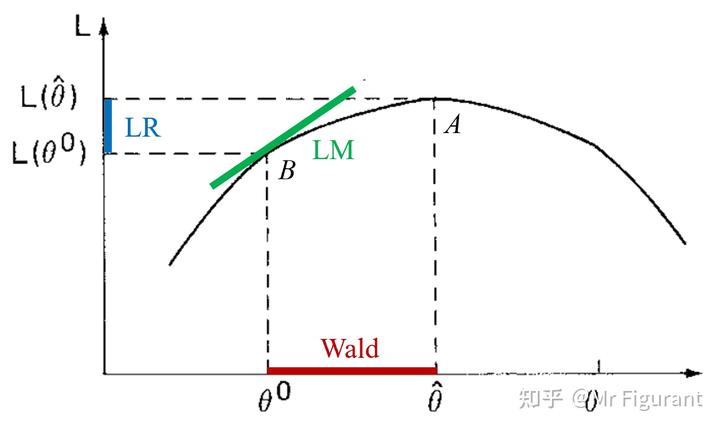
三个检验。图源:Engle(1984)模型预测
GARCH(1,1)模型的单步预测为:
h_{t+1} = \alpha_0 + \alpha_1 a_t^2 + \beta_1 h_t
两步预测为:
h_{t+2} = \alpha_0 + \alpha_1 a_{t+1}^2 + \beta_1 h_{t+1} ;
E(h_{t+2} | \Omega_t) = \alpha_0 + (\alpha_1 +\beta_1) h_{t+1} = \sigma^2 + (\alpha_1 + \beta_1) (h_{t+1} -\sigma^2)
多步预测为:
E(h_{t+h} | \Omega_t) = \sigma^2 + (\alpha_1 + \beta_1) ^{h-1}(h_{t+1} -\sigma^2)
若 (\alpha_1 + \beta_1) < 1 ,无论当前的波动率是多少,预测都会收敛到 \sigma^2 。很少或根本不更新长期波动。
定义预测误差为:
v_t = a_t ^2 - h_t = h_t (e_t ^2 -1 )
其中 v_t 为白噪声:
另一方面有 h_t = (r_t - \mu )^2 - v_t 。有:
(r_t -\mu)^2 = \alpha _ 0 +(\alpha_1 +\beta_1) (r_{t-1}-\mu)^2 + v_t - \beta_1 v_{t-1}
进而得到ARMA(1,1), (\alpha_1+\beta_1) < 1 时平稳。
模型扩展
(1)IGARCH(单位根GARCH)
与ARIMA模型类似,IGARCH模型的关键特征是:过去的平方冲击 (a_{t-i}^2-\sigma_{t-i}^2) 在 a_t^2 上是持久的。
IGARCH(1,1):
lGARCH可能是由波动率偶尔的水平变化引起的。
(2)GARCH-M(均值GARCH)
证券的回报可能取决于其波动性,期望更高的回报补偿风险。M代表GARCH的均值。GARCH(1,1)-M模型为:
其中, \gamma 称为风险溢价参数。因此,风险溢价的存在是某些历史股票收益具有序列相关性的另一个原因。通常假设误差的正态分布,但在应用中也会使用一些非正态分布,例如student-t分布和广义误差分布(GED)。通常,student-t误差假设给出了更好的估计。对于股票来说,不对称很重要的。然而,正态分布和student-t都是对称的,模型无法产生偏态分布。
(3)GJR-GARCH(TGARCH)(非对称GARCH)
非对称波动率来源于:
通常,负收益冲击对波动性的影响大于正收益冲击。GJR-GARCH模型可表示为:
h_t = \alpha_0 + \alpha_1 a_{t-1}^2 + \gamma I_{t-1} a_{t-1}^2 + \beta_1 h_{t-1}
为了得到理论结果,假设归一化残差具有对称分布,有 E(I_t)= 0.5 且 I_t 独立于 e_t 。模型可以写为:
h_t = \alpha_0 + [(\alpha_1 + \gamma I_{t-1})e_{t-1}^2 + \beta_1] h_{t-1}
取期望得到:
E(h_t ) = \alpha_0 + [(\alpha_1 + 0.5\gamma)+\beta_1] E(h_{t-1})
得到:
\displaystyle \sigma^2 = \frac{\alpha_0}{1-(\alpha_1 +0.5\gamma + \beta_1)}
(4)EGARCH(指数GARCH)
对于正态的 e_t :
\displaystyle E(|e_{t-1}| )= \sqrt{\frac{2}{\pi}}
对于student-t的 e_t :
\displaystyle E(|e_{t-1}| )= \frac{2 \sqrt{v-2} \ \Gamma (0.5 (v+1)) }{\sqrt \pi \ \Gamma (0.5v) (v-1)}
g(e) 由两条在 e = 0 处连接的直线定义。对于 g(e) 的函数:
从经验上看, \gamma 为负,表明当市场下行时,波动性增加更多。对于非对称波动率,收益分布是非对称的,并且在实证上具有较长的左尾。从长远来看,中心极限定理将减少这种影响,收益将近似正态。根据不同的数据频率,可以选择不同的模型。
3. 模型应用波动率期限结构
从时间 t 开始的资产 h 周期的对数回报是:
r_{t,h} = \displaystyle \sum_{i=1}^h r_{t+i}
得到:
\displaystyle Var(r_{t,h}|F_t) = \sum_{i=1}^h Var(r_{t+i}|F_t) + 2 \sum_{i=1} ^{h-1} \sum_{j=i+1}^h Cov [(r_{t+i},r_{t+j} )|F_t]
其中 F_t 表示时刻 t 的可用信息。日对数回报率的自协方差通常接近于0。在有效市场假设下,自协方差为0。
作为一个合理的近似:
\displaystyle Var(r_{t,h}|F_t) = \sum_{i=1}^h Var(r_{t+i}|F_t)
对于GARCH模型,先验近似表明:
\displaystyle \sigma_{t,h}^2 = \sum_{I=1 }^h \sigma_t ^2 (I)
其中, \sigma_{t,h}^2 表示 h 周期对数回报率在预测原点 t 处的条件方差。可以从GARCH模型的波动率预测中计算 h 期对数回报波动率。
时变相关与贝塔
(1)时变相关。用单变量GARCH模型来研究时变相关性。考虑两种资产回报 x_t,y_t :
因此有:
\displaystyle Cov(x_t, y_t) = \frac{Var(x_t + y_t) - Var(x_t - y_t)}{4}
这个等式对于条件协方差仍然成立。因此,资产收益 x_t,y_t 之间的时变协方差可以通过 x_t + y_t 和 x_t - y_t 的波动率得到。设 \sigma_{x+y,t},\sigma_{x-y,t},\sigma_{x,t} 分别为 x_t + y_t,x_t - y_t,x_t 的波动率。资产收益率 x_t,y_t 的时变相关性为:
\displaystyle \rho_t = \frac{\sigma_{x+y,t}^2 - \sigma_{x-y,t}^2}{4 \sigma_{x,t} \sigma_{y,t}}
(2)时变贝塔。统计模型在金融领域最常见的应用之一是资本资产定价模型(CAPM):
r_t = \alpha + \beta r_{m,t} + e_t , t=1,...,T
贝塔为:
\displaystyle \beta = \frac{Cov (r_t, r_{m,t})}{Var(r_{m,t})}
因此, \beta 的估计值取决于样本和市场指数 r_{m,t} 的选择。事实上,人们普遍认为 \beta 可能是时变的。GARCH模型可以用来对时变贝塔进行建模。其中, Cov (r_t, r_{m,t}) 可以从 r_t + r_{m,t} 和 r_t - r_{m,t} 的波动率得到。
最小方差投资组合
GARCH模型的另一个应用是估计资产收益的时变协方差,用于投资组合选择。把马科维茨的均值方差分析看作是投资组合分析。为简单起见,我们关注最小方差投资组合。假设投资组合中有 k 种风险资产,以投资组合收益的标准误差作为风险度量。
最小方差组合的思想是选择权重 w_t 作为以下简单优化问题的解:
\displaystyle \min_w \ w'V_t w ,s.t. \displaystyle \sum_{i=1}^k w_i = 1
解决上述问题,就得到了最优权重(如果允许卖空):
\displaystyle w_t = \frac{V_t ^{-1} \bm1}{\bm1' V_t ^{-1} \bm 1}
其中 \bm 1 为1的 k 维向量。
在实践中,权重将取决于用于估计 V_t 的样本。可以使用上述程序来估计两种资产收益之间的协方差。然后使用这些两两协方差估计来构建投资组合中所有资产的 V_t 估计。这种协方差矩阵估计方法的一个可能缺点是,得到的协方差矩阵 V_t 可能不是正定的。然而,对于小 k 和大 T ,期望 V_t 是正定的。
对于给定的 t ,用GARCH(1,1)模型对单个资产收益及其和、差进行估计。然后得到最小方差的投资组合,并使用权重来计算t+1的投资组合收益。在时间t+1中重复估计过程,以计算t+2时的投资组合回报。即估计 V_t ,获得新的权重,每天重新平衡投资组合。
代码附录参考文献Ruey S. Tsay, Analysis of Financial Time Series, 3rd, John Wiley & Sons, 2010.继续学习
(完)
参考Engle, R. F. (1984). Chapter 13 Wald, likelihood ratio, and Lagrange multiplier tests in econometrics. Handbook of Econometrics, 775–826.(84)02005-5

发表评论