mahout的推荐主要是基于协同过滤,协同过滤是通过了解用户与物品之间的关系,也就是用户对物品的偏好来总结经验(无需了解物品的属性),从而进行推荐。
而协同过滤又分为基于用户和基于物品。
基于用户是寻找用户与用户之间的相似度,如A用户和B用户都喜欢a,b,c物品,那么可以认为A和B用户很相似,如果A还喜欢d物品,那么B很有可能也喜欢d物品,因此可以推荐d物品给B用户。
基于物品是寻找物品与物品之间的相似度。如a和b物品同时被A,B,C用户喜欢,则可以认为a和b物品很相似,如果D用户还喜欢a物品,那么D用户也很有可能也喜欢b物品。
mahout的推荐系统由多个组建混搭而成,我们可以根据自己的需求和场景选择最适合自己的组建来搭配。下面介绍基于用户的,通常包括如下组建:
数据模型:由DataModel的子类实现
用户间的相似性度量:由UserSimilarity的子类实现。
用户领域的定义:由UserNeighborhood的子类实现。
推荐引擎:由Recommender的子类实现。
下面开始介绍计算用户相似度的各种算法:
首先有数据如下:
横排是物品,竖列是用户,中间的是用户对物品的评分,5分是很喜欢,3分是一般,1分是讨厌。 没有得到用户对该物品的偏好。
1,101,5
1,102,3
1,103,2.5
2,101,2
2,102,2.5
2,103,5
2,104,2
3,101,2.5
3,104,4
3,105,4.5
3,107,5
4,101,5
4,103,3
4,104,4.5
4,106,4
5,101,4
5,102,3
5,103,2
5,104,4
5,105,3.5
5,106,4
1. 基于皮尔逊相关系数的相似度
皮尔逊相关系数是一个介于-1和1之间的数,它度量两个一一对应的数列之间的线性关系度量,也就是说,它表示两个数列中对应数字一起增大或一起减小的可能性。当接近于1时,表明他们数字变化趋势一致,当接近于0时,变化趋势没什么关系,当接近于-1时,变化趋势是相反的。
公式如下:
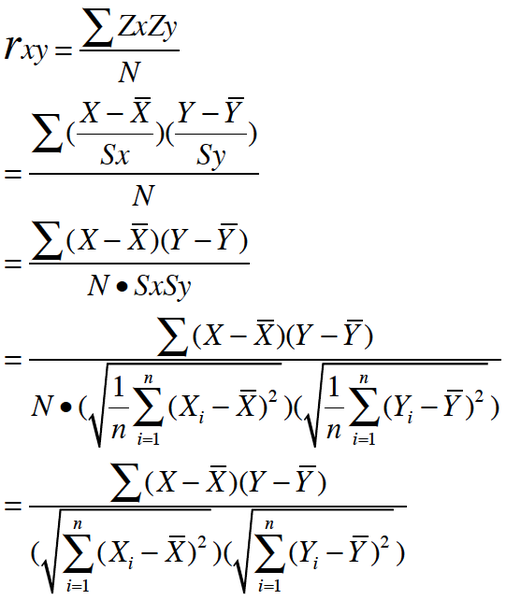
从最下面的公式能看得出来,pearson就是把两个向量减去他们的平均值后,计算他们夹角的cos。当然夹角越小,两个向量的方向越一致。
在基于用户的协同过滤中,我们把一个用户对所有物品的评价联合起来,看作向量。
如计算上面用户1和5的相似度。他们都评价了101,102,103,把这些评价组合成向量,则用户1的向量是(5,3,2.5),用户5的向量是(4,3,2),然后套入上面的公式,向量1的平均值是3.5,向量5的平均值是3. 分子是向量的点乘得出是2.5.分母是两个向量的长度相乘是2.64.再相除得到pearson相似系数为0.945。

用户1和3只共同评价了一个物品,所以不能得出他们间的pearson相关系数。
缺点:没有考虑两个用户同时给出偏好值的物品数量。如1和4只同时给出了两个物品的偏好,但他们的pearson相似度还高于5(5和1同时给出了3个物品的偏好),这跟直观感觉不一致。
1.不能计算两个用户只同时给出了一个物品的偏好值。2.如果一个用户给所有物品的偏好都一样,也不能算他与别人的相似度(代入上面的公式就知道)。因此在小的或疏松的数据集中,比较有问题。
为了解决上面的问题,可以加入权重(weighting),即基于较多物品计算相关系数时,使正相关值向1靠近,使负相关值向-1靠近。基于较少物品时,使相关系数向均值靠近。
2. 基于欧式距离定义相似度
可以将用户想象为多维空间的点(维数等于物品数),偏好值是他们的坐标。这种相似度量就是计算两个用户点间的欧式距离d。他们越远代表越不相似,越近越相似。
公式为:
可以先看看平面两点距离计算公式,就容易看懂了。实际应用中将1/(1+d)作为相似度,那么就是越接近于1越相似,越接近于0越不相似。

3.基于余弦相似性度量
和欧式距离一样,也将用户偏好值视为空间的点,不过这次不是计算他们的距离了,而是从原点出发,分别连接这两点,把他们看作向量,计算他们夹角的余弦。他们的夹角越小则越相似,夹角越大则越不相似。
可以看出来,余弦相似度就是两个向量的点乘除以他们长度的乘积。跟pearson相似度的公式差不多,只是没有减去他们的均值。
余弦相似度对数值的绝对值不敏感,例如A用户对两个物品的偏好是1,2。B用户的偏好是4,5。这时分两种情况,每个人都有自己的一套评分标准,有的人喜欢打高分,有的人喜欢打低分。那么如果这里A是喜欢打低分的人,B是喜欢打高分的人,虽然他们这里打的分有点悬殊,但实际上他们的评价还是比较一致的,那么他们比较相似。这是一种情况,另外的一种情况就是他们打分的标准都差不多,那么这里显然A用户是不喜欢这两个物品,而B用户是喜欢他们的。
但是这里的余弦相似度却高达0.98,因此需要对数据去中心化的处理,也就是对数值减去他们的均值,对于上面说的第一种情况,如果A用户给出所有物品的评分均值是1(因为他喜欢打低分),那么他对这两个物品的评分会调整为0,1,B用户给出所有物品的评分均值是4,那么他对这两个物品的评分会调整为0,1。这时候再计算余弦相似度就会达到1了,说明这两个用户确实很相似。对于第二种情况,如果A和B用户给出所有评分均值都是3,那么分别调整为(-2,-1)和(1,2)。这时他的余弦相似是-0.8了。这样就知道他们确实不相似了。
mahout会对数据输入进行中心化处理(也就是减去均值),因此mahout余弦相似度的实现和pearson相关系数是一样的。不过也同样给出了一个没有中心化处理的余弦相似度实现UncenteredCosineSimilarity。
4.斯皮尔曼相关系数
这个是pearson相关系数的一个变体,他根据用户的评分对该用户喜欢的物品做了个排序,然后用这个排序重写他的偏好值。如排最后一名的物品重新给偏好值为1.,倒数第二的重给偏好值为2,以此类推,最喜欢的偏好值最高。因此这种算法丢弃了用户偏好的具体值,而仅仅保留了其顺序。
然后再用spearson进行计算。如下:

这种计算方式性能很差,因为需要为每个用户进行排序,数据规模大的时候不理想,意义不大。
5.古本系数计算相似度
这个算法不关心用户对一个物品的偏好是高是低,他只关心两个用户一起评论了多少个物品。
他认为两个人同时评价了200部电影比同时评价了2部电影的相似度要高,哪怕他们给这两部电影的评分很一致,而给200部评分的不太一致。
他的公式如下:
分子是他们的交集的数量,分母是他们并集的数量。
如用户1和用户5,交集数为3个物品,并集数为6个物品,那么相似度就是0.5。

6.对数似然比
跟谷本相似度差不多,也不考虑偏好值的多少,只关心同时有的偏好。
不过它试图反映两个用户由于机缘巧合发生重叠的不可能性。也就是说两部电影两个用户评论了,但是就只有他们两个评论了,那么这是机缘巧合他们一起评论的可能性就很低,因为别人都没评论,也就相似了。如果这两部电影也很多人别人评论了,那么这是机缘巧合的概率就大了,因为大家都评论了,他们也就不相似了。
总结
使用GroupLens网站的数据做了实验,使用1000万的用户对电影的偏好数据。
下面是实验结果的数据:
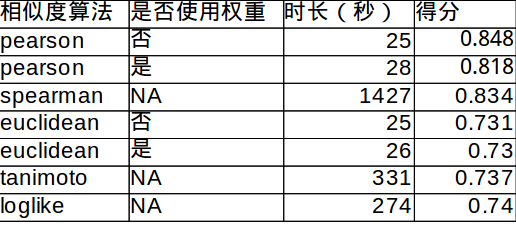
得分是推荐结果与实际结果的误差大小,数值越小,正确率越高。可以看出用了权重的欧式距离在这个实验中正确率最高。
使用的测试代码如下:
public class GroupLens10MEvalIntro
{
static DataModel model;
static RecommenderEvaluator evaluator;
static RecommenderBuilder recommenderBuilder;
static String similarityName;
@BeforeClass
public static void onStart() throws IOException
{
RandomUtils.useTestSeed();
model = new GroupLensDataModel(new File(FilePath.CF_10M));
evaluator = new AverageAbsoluteDifferenceRecommenderEvaluator();
}
@Test
public void pearson()
{
similarityName="PearsonCorrelationSimilarity";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new PearsonCorrelationSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void pearsonWithWeight()
{
similarityName="PearsonCorrelationSimilarityWithWeight";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new PearsonCorrelationSimilarity(model, Weighting.WEIGHTED);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void euclidean()
{
similarityName="EuclideanDistanceSimilarity";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new EuclideanDistanceSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void euclideanWithWeight()
{
similarityName="EuclideanDistanceSimilarityWithWeight";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new EuclideanDistanceSimilarity(model, Weighting.WEIGHTED);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void spearman()
{
similarityName="SpearmanCorrelationSimilarity";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new SpearmanCorrelationSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void tanimoto()
{
similarityName="TanimotoCoefficientSimilarity";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new TanimotoCoefficientSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@Test
public void loglike()
{
similarityName="LogLikelihoodSimilarity";
recommenderBuilder = new RecommenderBuilder()
{
@Override
public Recommender buildRecommender(DataModel model) throws TasteException
{
UserSimilarity similarity = new LogLikelihoodSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(100, similarity, model);
return new GenericUserBasedRecommender(model, neighborhood, similarity);
}
};
}
@After
public void evaluator() throws TasteException
{
double score = evaluator.evaluate(recommenderBuilder, null, model, 0.95, 0.05);
System.out.println(similarityName + ":" + score);
}
}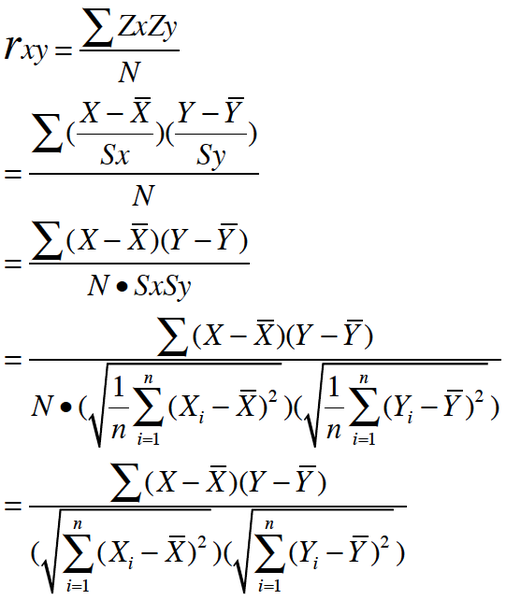
发表评论