
本文有视频版!更生动直观!
点这里→竟然有人质疑古人的智慧?农历到底怎么来的?且看神奇“四分历”!
系统梳理中华文化,给你真正文化自信
什么最能体现一个民族的文化水平?什么能称得上古代文明的标志?我个人首推历法。
为什么李约瑟曾称中国人为“全世界最坚毅、最精明的天文观测者”?他会不会吹过头了?我们的祖先真有这么厉害么?要想证明这些,只需了解一部最神奇的古代“四分历”。
关于“四分历”,什么是四分?春秋时代古人测出的平均回归年长,也就是从一个冬至到下个冬至的时间为365¼日,古称“岁实”,四分就是这个¼。为什么我刚说这是“神奇”的四分历?因为只要有了这一个小小的数据,我们就可以用各种巧妙的方法,推出历法其它数据,制定出所有完整的历谱!
诶,你可别觉得我在瞎吹,这事没那么难,现在我就可以手把手地带你制历。

准备制历——
因为历法是要调配年月日,一个太阳年的长度比十二个朔望月的长度要长11天多,三年就多了一个月,这就需要插个闰月,让一年四季与月亮运行周期大体相等。所以要想制定历法,还必须知道月亮的周期,也就是一个阴晴圆缺的朔望月长度。那如何用回归年长推出每个月的长度呢?
最方便的就是把时间线拉长求平均值。我们可以先设定一个最完美的年月日调和状态。在这段时间里,阳历和阴历的时间总长度完全相等。
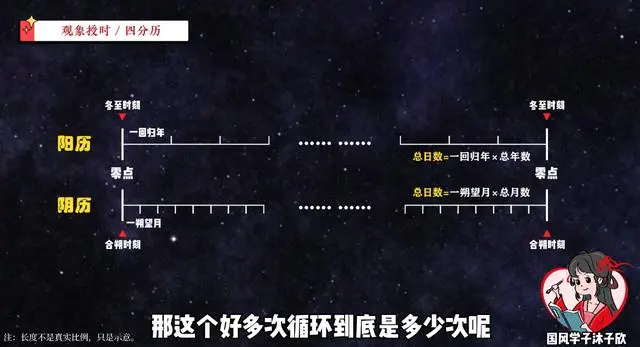
假设起点都是某天的夜半零点,我们先让冬至时刻,也就是太阳年的起算点,在经历了好多好多次循环后,再次回到了某天的夜半零点;然后让日月的合朔时刻,也就是朔望月的起算点,在经历了好多好多次循环后,也回到了这天的夜半零点,这样它们的起点和终点就能完全对齐,所经历的天数也都完完整整刚好相等。
接着我们就可以用已知的平均回归年长算出总天数,再除以总的朔望月数量,不就能算出每个月的平均长度了嘛!
那这个好多次循环到底是多少次呢?上一期讲到,春秋中期的古人就已经摸索出了19年7闰的规律,也就是说在19年里加7个闰月,就可以让阳历和阴历的总长度大体相等。所以我们来试一下19年7闰。
用每年有365¼日来算,19年一共有6939¾日,不是个整数,也就是说冬至时刻经过19年的循环,回到的不是零点,而是得再过¾天,在傍晚六点,这就无法整齐地对应上日数。那怎么把后面的分数消掉呢?
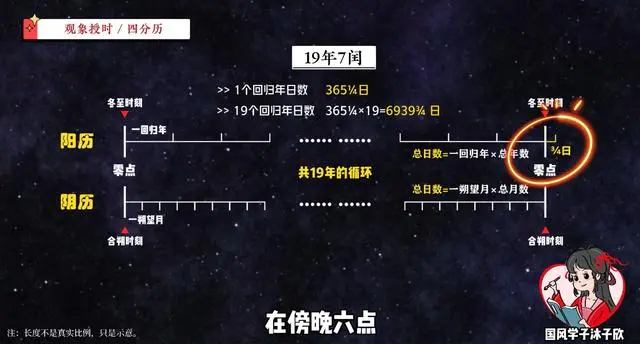
最简单的就是把这个循环再扩大4倍,这样回归年的天数就能取整。也就是说过了4个19年,即76年后,冬至时刻终于又回到了零点,这段时间里一共有完完整整的27759日。
那么对应的,这段阴历的时间也刚好经历了完完整整的27759日,而这76年里的总月份是,12x76=912个月,再加上28个闰月,一共是940个朔望月,于是总日数除以总月数,就得到了每个月的平均时间为29又499/940日,古称为“朔策”。
于是,我们就有了比较精准的回归年长和朔望月长,接着就可以开始制定历法啦!

开始制历——
第一步我们得先确定每个月的起点,其实很简单,既然每个月的长度都知道了,那只要不断叠加上去不就行了嘛!
我们先定第一个月的起点,因为最初历法起算点是冬至,而冬至所在月都是子月,所以我们把子月的朔日作为第一个月的第一天。这里解释下,子月就是夏历,即现在农历里前一年的十一月。关于子月和夏历以及三正的知识点,可以复习【探索时间】篇章的纪月法那期。(在这→《揭秘夏商周!迷惑世人千年的三正论!「中国天文史·探索时间」02》)

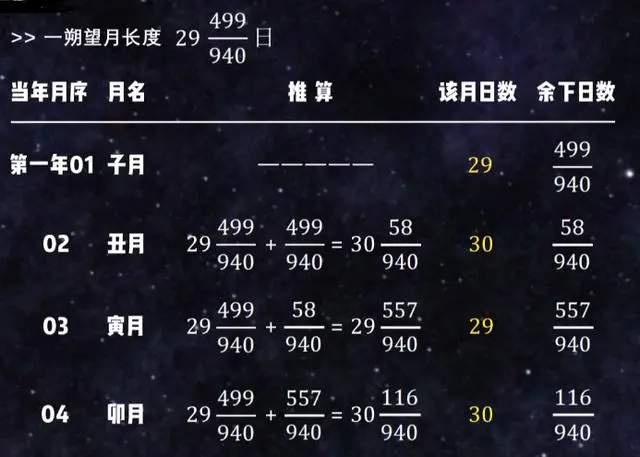
那这个月有多少天呢?因为朔策为29又499/940日,而天数又必须要取整,所以一般是小月29日、大月30日交替排布。我们可以设第一个月为29日,那这个月就还余下499/940日,需要放到第二个月里。
第二个月丑月的长度本身就是29又499/940日,再加上上个月余下的日子,就是30又58/940日,那么就取整,把这个月设为大月30日,余下的这58/940日,继续加到下个月。
第三个月寅月本身的日子,加上上个月余下的日子,就是29又557/940日,取整后这个月为小月29日,余下的继续加到下个月。
同理第四个月卯月算出来就是30又116/940日,取整为大月30日。这时我们已经可以看到是小月大月交替排布了。
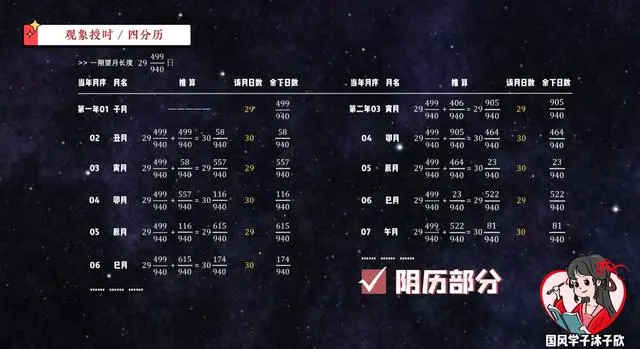
接下来都是一样不断叠加。一直加到第二年的第五个月辰月时,就会发现这个月是大月30日,而上个月也是大月30日,这,就是阴历里常有的连大月。
接着我们再照常把余下的日子加到下个月巳月,得出巳月为小月29日,就这么一直不断不断加下去,就可以排出历法的阴历部分了。
那阳历部分呢?中国的阳历就是二十四节气,所以下一步就是确定每个节气的时刻。其实也很简单。就像之前说的,按照平气的办法,只要把一回归年时间平均分成二十四份,就能得到二十四节气了。
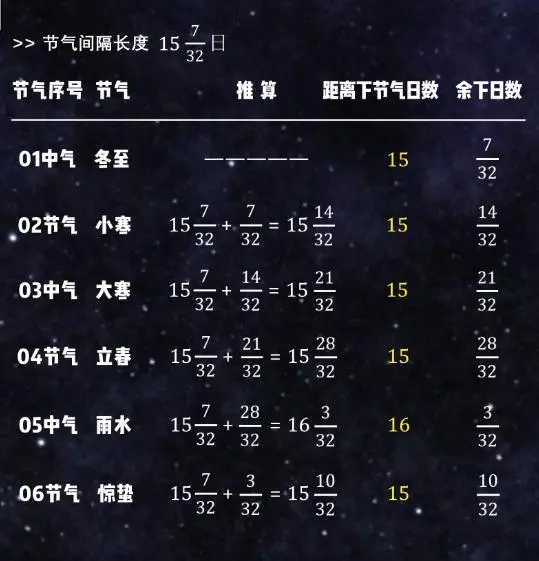
一回归年是365¼日,除以24,也就是说每过15又7/32日就交一个新的节气。而天数必须取整,所以每个节气之间不是15日就是16日。
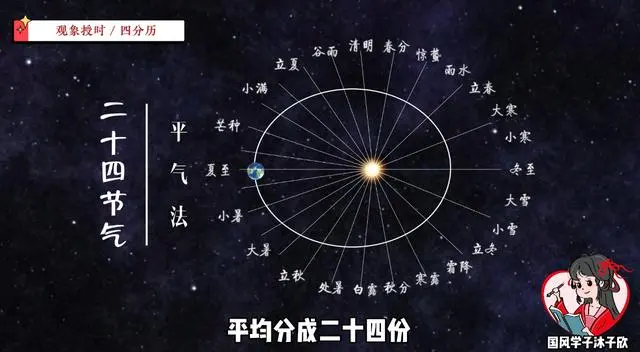
接下来就和算月份一样,我们把古代历法的起算点,也就是冬至点作为第一个节气,设定15日后为下个节气小寒,余下的7/32日就加到下个节气。
到下个节气本身就有15又7/32日,再加上前面余下的7/32日,就是15又14/32日,取整为15日,那么过15日后就是下个节气大寒。
这样再排两个节气之后,就会遇到16又3/32日,这时取整为16日,也就是说从雨水过后要经过16天才会到惊蛰。接着再这么一直不断叠加下去,就能排出所有的节气了。
就是这么简单,阳历和阴历的部分全都排出来了。下面最关键的来了,怎么调和年月,安插闰月呢?
其实也不难,上期说过,置闰的规则是“无中气置闰”,只要我们把阴阳两个历放在一起一对比,找出哪个月里没有中气就行了。

按照中国人的制历习惯,历法的起点必须很特殊,一般都是冬至(或立春)和日月合朔同时发生的时刻,这个时刻就定为“历元”。而我们刚刚推的两个历的起点正是冬至和朔日,所以只要把这两个历的起点对齐就是历元了。
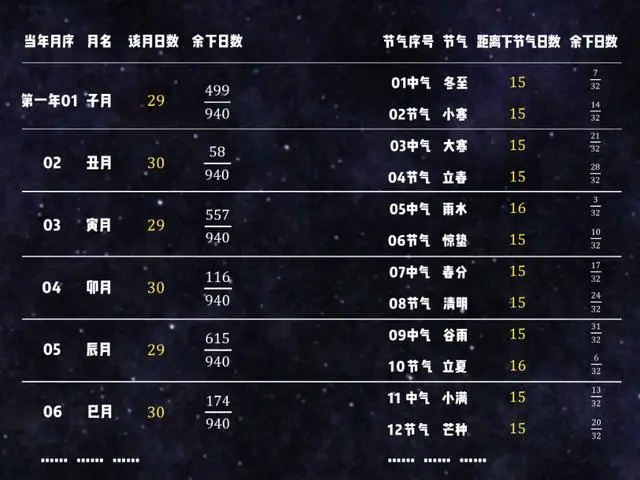
这样一个个对比着看,就会发现第三年的第九个月申月,大暑这个中气刚好在申月前一天,后一个中气处暑刚好在下个月第一天,申月里面只有一个节气立秋,并没有中气,所以这个月就要变成闰月,名字就取前一个月的名,叫做闰未月,下个月再设为申月。

好了,现在我们有了每个朔望月的时间点,每个节气的时间点,以及闰月的位置,最后还需要加上每天的日期,这就要用上我们的干支纪日。
60个干支为一周期,每个干支记一天。为了满足历元的特殊性,一般都是把干支的首日,也就是甲子日设为历元,然后再按六十甲子的顺序一天天排下来。
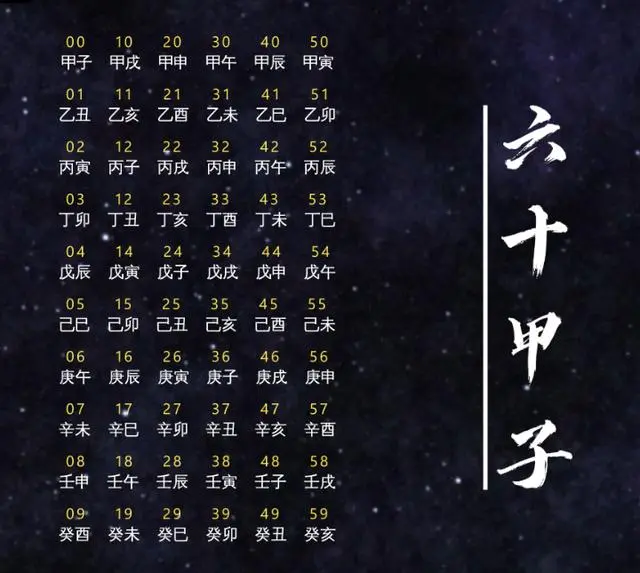
现在,我们把刚刚算的所有时间点都写上对应的干支日,为了方便,我就只写干支的序号,甲子日为0号,最后一个癸亥日为59号。至于为什么不是从1到60,这里先埋个伏笔。就这样,一份完整的历谱终于诞生了!
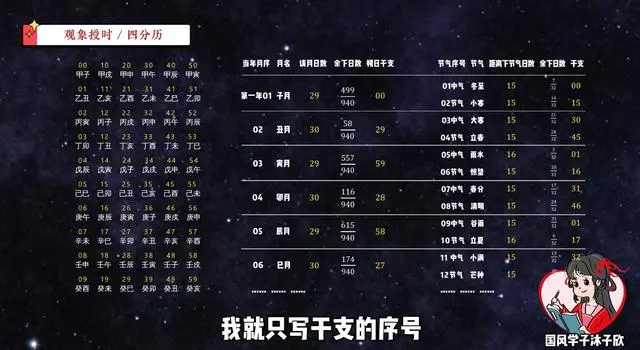
按道理,只要这样一直不断叠加下去,我们可以排出很多年很多年的历谱,可是这也太累了吧!如果能找出一个规律的周期,是不是就可以一直循环套用?那这样岂不是可以很方便推出十年百年甚至上千年的日历?
是的,这就是四分历所做的事情。古人把制历叫做推步学,就是这个意思。

寻找完美周期——
其实关于周期,我们刚刚已经得到了两个周期。
一个是19年7闰,古人称其“一章”。在这一章里,阳历和阴历的长度是能大体吻合的。假设历元是甲子日夜半零点,也就是甲子日甲子时,同时也是合朔冬至时刻,那么在一章过后,合朔日和冬至日都会走到同一天,但那天并不是甲子日而是癸卯日,也不会回到同一时刻。所以这并不是一个理想的周期。
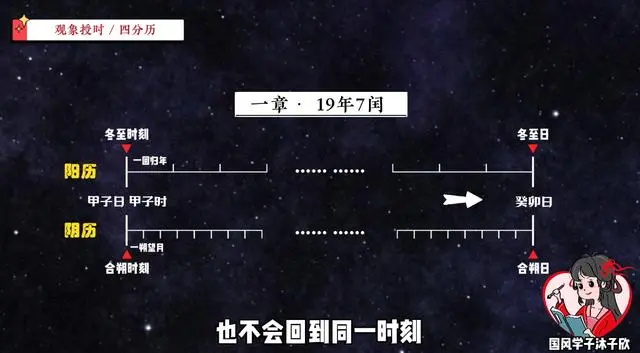
第二个周期是把章扩大4倍,也就是76年,古人称其“一蔀”,从历元开始,经一蔀过后,合朔时刻和冬至时刻都能回到夜半零点,这周期看起来行。
但古人制历都是用的干支纪日。一蔀76年里共有27759日,而干支是60日一周期,两个一除,又不是一个整数,还余下13/20个周期,也就是39日。这说明经一蔀之后,合朔和冬至虽然都回到了零点,但不是甲子日的零点,而是要再经过39个干支日,到了癸卯日的零点。
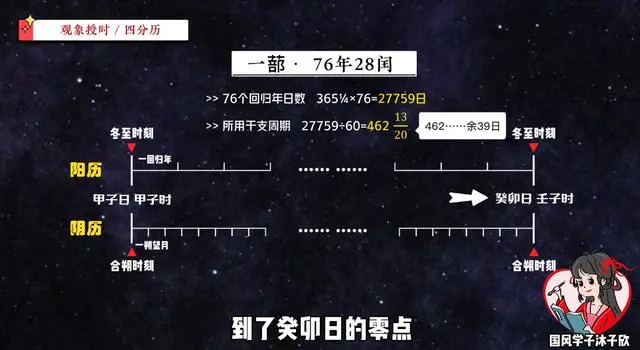
那到底要怎样才能在一个周期里,塞下完整的60干支这个套餐呢?其实很简单,道理跟刚才一样,把周期再扩大20倍,把后面的分数消掉就好了。
76年扩大20倍就是1520年,古人称其“一纪”,也就是说,经一纪之后,合朔和冬至时刻都回到了甲子日的夜半零点,即甲子日甲子时。
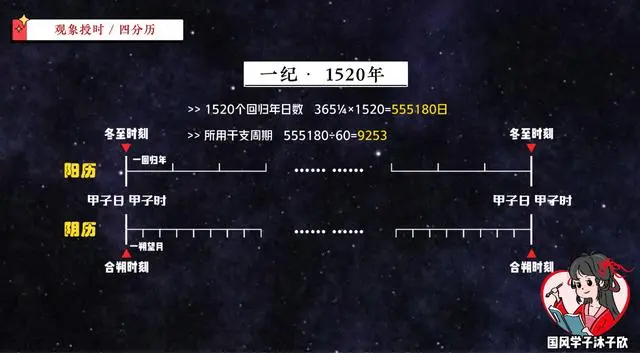
那能不能再完美一点,让它们的起点和终点都是甲子年甲子月甲子日甲子时呢?
诶,这时候可能懂点干支的人就要反驳我了,哪有这个时候啊!
按干支规律的五虎遁来看,甲年里只有丙子月,甲子月只有在戊年或者癸年里才有,根本没有甲子年甲子月!
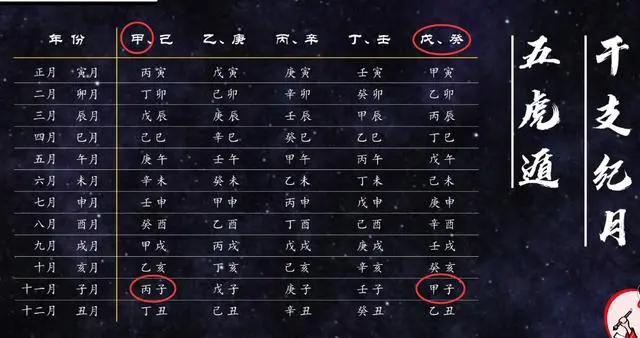
按常理来讲是没有,除了一种情况。这个五虎遁是用夏正排的,把寅月作为正月的话,确实是这样,但我之前也说过,春秋战国时代,也就是四分历行用那会,各国岁首不一,有所谓“三正”之说,如果我用的是子正,也就是把子月当做正月呢?甲子年的正月不就是甲子月了吗?
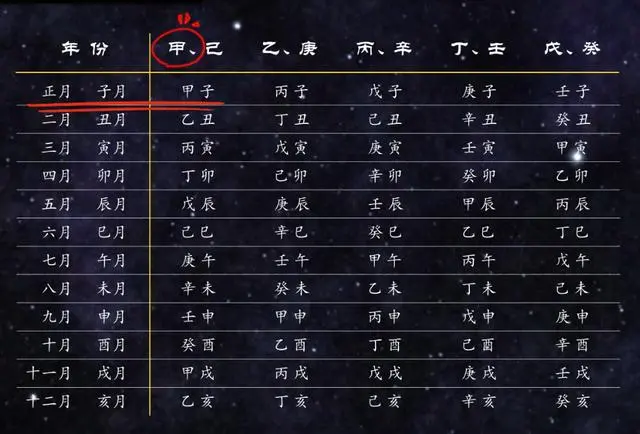
好的,那怎样的周期才能让合朔和冬至的起点和终点,都是甲子年甲子月甲子日甲子时呢?
刚才我们是要在一个周期里塞下完整的60干支日套餐,所以用总日数除以60,现在要在一个周期里塞下完整的60干支年和干支月套餐,那只要把总年数和总月数除以60就行了。
1520年里只能塞下25⅓个干支套餐,18800个月里只能塞下313⅓个干支套餐,所以只要把周期再扩大3倍,不就能把这两个分数都消掉取整了嘛!
1520年再扩大3倍就是4560年,古人称其“一元”,从历元起经过一元后,最完美的周期出现了!合朔和冬至时刻终于又回到了甲子年甲子月甲子日甲子时!

推千岁之历——
接着我们就可以用这几个周期来循环套出历谱了,具体怎么做呢?
可以先用小周期推出大周期,比如刚才的一蔀,虽然经过这76年后,合朔冬至回到的不是甲子日,但起码还是回到了零点,起码这段时间里是有完完整整的天数的,只是干支不同罢了。所以我们可以从一蔀出发,去推一纪。

刚才已经算出,一蔀的总日数除以60干支日套餐后,还有39的余数,这个叫“蔀余”。也就是说这个蔀的最后一日是第39位干支壬寅日,那么下个蔀的首日就是癸卯日。
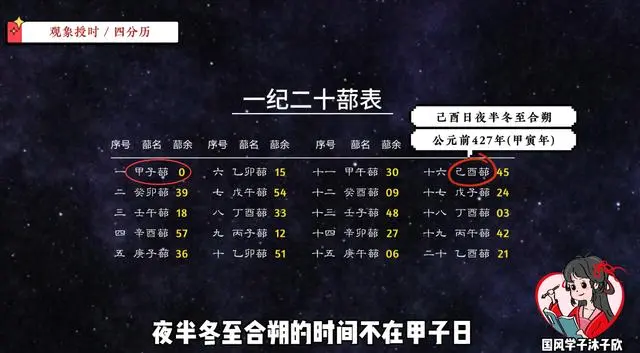
我们可以记录下来,把每个蔀首日的干支当做这个蔀的名字,后面记录上个蔀留下的蔀余,之后每蔀都把39这个余数叠加上去,满60甲子就进一位,这样就能排出一纪二十蔀每个蔀的首日干支了。
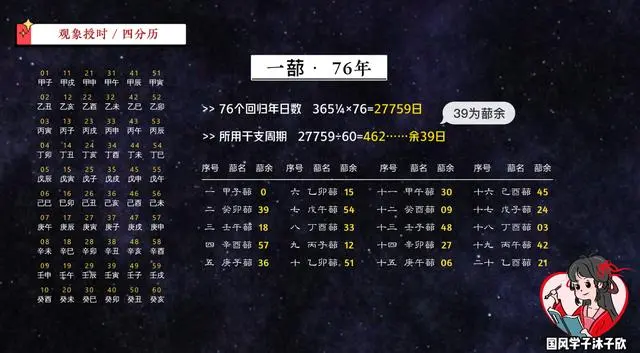
这时你会发现,每个蔀首的干支本身的位数都比后面的蔀余大一位,所以为了对照方便,我们把干支对应的序号都减一位。这也就是我刚才制历的时候,让甲子日为0号,癸亥日为59号的原因了。
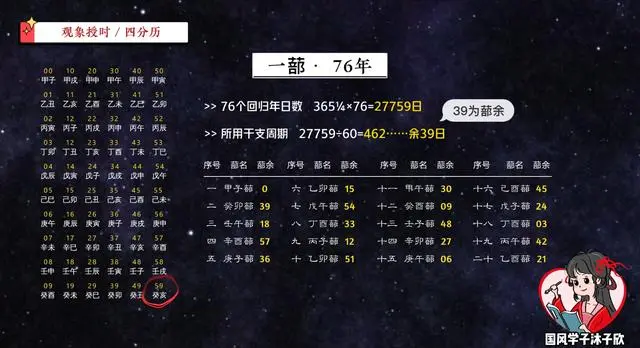
有了这个一纪二十蔀表,只要我们推算好第一个甲子蔀76年的所有历谱,那么其余十九个蔀的历谱都能照抄第一蔀,只是算具体干支日的时候,加上后面的蔀余就行了。那么同理,一元三纪也能照此推出。
于是,我们从一个小小的回归年365¼日,推出了朔望月和节气的长度,推出了一章19年的朔闰历谱,继而又推出了一蔀76年,一纪1520年,直至一元4560年的所有历谱!甚至我们还可以拿着这一元的完美周期,去推测更长远的过去和未来!

以四分之术,推一“章”之法,制千岁之历。为什么叫四分历?什么叫做“章法”?什么才叫“历法”?大家有目共睹。而这些竟然都是中国人在两千年多前就做到的!证据就是这份曾被埋没了千年的“天书”。

揭秘天书——
《史记·历术甲子篇》,虽然名字写着“历术”,但内容看起来却与历法毫无关系,而且又有一堆莫名其妙的字眼和数字,让后世甚为不解,导致这份本应成为“中华宝典”的资料,长期被埋没在历史的尘垢中。不过只要我们用四分历的角度去看,就能揭开这份“天书”的神秘面纱。

首先看它的名字叫做“甲子篇”,就是说这里记载的是第一部甲子蔀76年的推算过程。要想用其证明四分历,只要把它和我们刚刚算的数据对比一下就知道了。
它的格式是这样的,每年都只有短短的三行,我可以先告诉你,这第一行写的是年份以及这年的月数,后面两行大余小余写的分别是合朔的时刻和冬至的时刻。

这是第一年的原文记录,第一年作为历元比较特殊有四行啊。

“元年”,指四分历甲子蔀的第一年;“岁名焉逢摄提格”,这个其实我们在之前【纪年法】那期(这里→《解密纪年密码!啥是岁阴岁阳?生肖怎么来的?「探索时间」04》)里讲过,这些奇怪的名字就是干支的别名,我们对照表格就知道了,“焉逢”是甲,“摄提格”是寅,所以这年是甲寅年。

“月名毕聚”,《尔雅·释天》解释“毕聚”指甲子,所以这个月是甲子月; “日得甲子”指这天是甲子日;“夜半朔旦冬至”,“旦”字是后人妄加的,我们可以忽略,这句是说这天夜半子时零点合朔冬至。
所以这整句翻译过来就是甲寅年甲子月甲子日甲子时合朔冬至,是个比较完美的历元。
不过为什么是从甲寅年开始而不是甲子年呢?这点我也没找到原因,有知道的高手可以评论区讨论讨论。

第二行的“正北”,在二十四方位里指子位,对应的是零点子时。后面的“十二”指这年有十二个月,我们刚刚制历的时候第一年就是平年十二个月,没错,对上了。
那后面两行为什么写“无大余、无小余”呢?其实这个“余”跟刚刚说的“蔀余”差不多,都是上一个周期留下来的余数,因为这是历元,是历法的起点,当然就是无余数啦。
第一年数据都归零,我们也看不出什么,要想证明刚刚的四分历算法,重点得看后面的。

第二年原文写“端蒙单阏二年”,查表可知这是乙卯年,一共有十二个月,我们刚推的历第二年也是平年,对得上。
第二行写的是这年第一个月合朔的时间,“大余”看的是干支日,“小余”看的是时刻。刚刚算的数据里,第二年子月的第一天对应的序号是54,就如同二十蔀表里的蔀余一样,这个序号是指上一个周期的干支余数,而原文写的正巧就是“大余五十四”;再看“小余”,这是上一个周期留下来的时间,我们刚刚算的是348/940日,而原文里写的是“小余三百四十八”,正巧就是我们的分子!
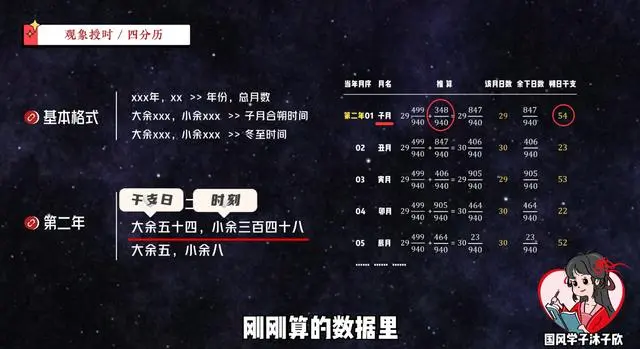
我们再试试下一行,这写的是这年冬至的时间。刚刚算的第二年冬至这天,序号是5,上个节气余下的时间是8/32日,而原文是“大余五,小余八”,又双叕对上了!
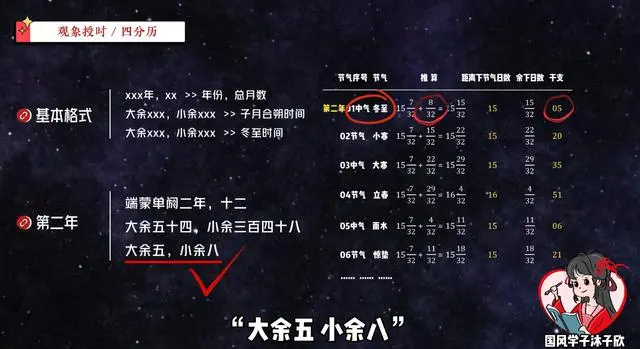
这难道是巧合吗?要不我们再来对一年吧。
第三年翻译过来是丙辰年,“闰十三”指这年为闰年共有十三个月,诶,我们刚算的第三年刚好就是闰年!

第三年的子月合朔日序号是48,上个月的余数是696/940日,原文写的也是“大余四十八,小余六百九十六”!
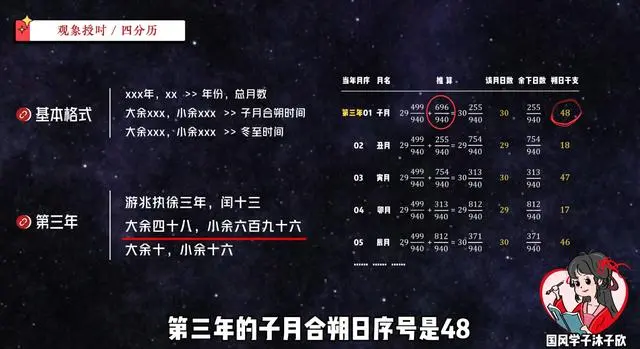
第三年的冬至日序号是10,上个节气的余数是16/32日,原文正正好就是“大余十,小余十六”!!!
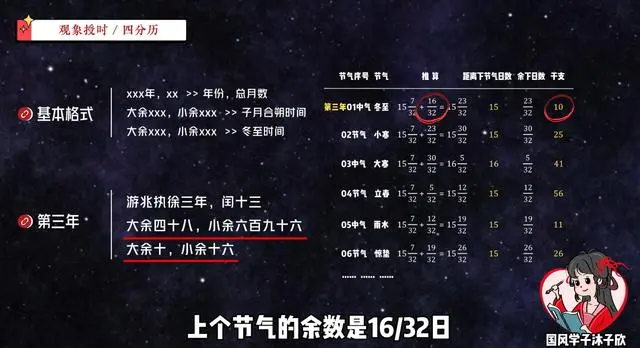
一两年可以算巧合,那三年还能算巧合吗?
有学者甚至把整个76年的数据全都核对了一遍,竟然发现所有数据都能对得上!历历分明,证据确凿,这份困扰了世人千年的“天书”,原来就是四分历的运算宝典!
那时的人们只要拿着这一蔀76年的数据,就可以推出一元4560年甚至更久更久的所有历谱!

说到这我就很好奇了,到底是谁创制了这么神奇的宝典?这书是出自《史记》,难道是司马迁?
实际上,四分历的创制比《史记》早多了。据天文大家张汝舟考证,四分历是从战国初期公元前427年开始施行的,正是甲寅年,但那年只是第十六蔀己酉蔀的首年,夜半冬至合朔的时间不在甲子日,显然不配称为历元。
于是四分历的创制者便以此为基点,运用四分术逆推得出的历元为公元前1567年,那时正是甲寅年甲子月甲子日甲子时冬至合朔。也许四分历从甲寅年开始算起就与这个有关吧。
可以想象,中华历法在积累了千百年的实践经验后,终于总结上升为系统的理论,并在公元前427年于某位或某几位天文大家的手里,汇成果于四分历,从此让中国进入了真正的历法时代。
如此优秀的历法一经创制,就必然会风靡各国。谁会舍弃先进的历法而去吃观象授时的苦头呢?况且战国的士大夫们一个个都朝秦暮楚,历法一经行用自然不受国界的约束。总有人认为战国时代各国历法不同,其实它们的内核都是四分历,只是岁首和建正不同而已。

所以,在司马迁写《史记》那会,四分历就已经广泛行用了三百多年,早已得到公认,司马迁只是采自史官旧牒,随文记录而已。不过也正是有了他这珍贵的一手资料,我们才能拭去历史的尘埃,亲眼见证到古代劳动人民的勤劳和智慧,见证到中国历法的生命力之所在。
孟子曾充满自信地说:“天之高也,星辰之远也,苟求其故,千岁之日至,可坐而致也。”这正是当时人们运用四分历推算年岁的真实写照。尽管后世还是因为各种原因选择了改历,但都始终无法撼动四分历作为中国天文史上第一部真正历法的奠基地位。

这会可能有人要反驳说这不是第一部历法,不是还有更古的古六历吗?那么下期我就来讲讲这所谓的古六历。
最后总结下这期的笔记,今天干货满满,建议循环食用。我是国风学子沐子欣,记得关注,一起为中华之崛起而读书!

温馨提示:本文为原创系列【中国天文史】之历法变迁第01篇:四分历。本文视频版的解析更直观清晰哦!放在开头了~

发表评论