我觉得最重要的是你的诉求是什么，是想去一个很好的大学，还是更想确保能考上。

如果是第一种，我的建议就是，哪个好考就考哪个吧。

既然你想考一个好学校，那我们可以看看2021年一二本学校各招考类别的录取率：

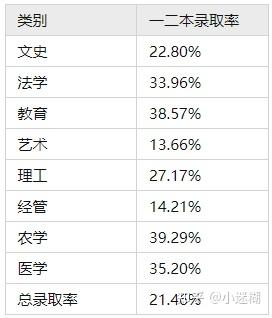
其实从总录取率来看，经管确实比文史好考。但是单从一二本的录取率来看，文史类上岸率是要更高的。

这主要是因为一二本的院校文史类会招的更多，而经管类三本院校会招的很多。

但是如果你更想确保能考上，我是更建议去报经管的，比较保险，就业面也大一些。

还有就是有些学校会对英语能力和专科时所学的专业有所限制，报名的时候要注意好好看一看。

总体来说，文史类的报考限制会更多一些，经管要少很多。

我的建议是报经管吧，理由如下：

1.投档线低。文史的投档线被称为魔鬼投档线，每年都非常高。但经管的投档线就低很多，偶尔的时候会非常低。这也就保证了你就算考不上特别好的学校，其他的选择范围会广很多。

2.数学提分快。语文成绩很难拉分，成绩相差不会很大，但想要提分真的很难。因为语文还要靠平时的积累，也不是背会了就能考好的。但是数学提分就挺快的，理解了细心点考高分还是比较容易的。不过也不排除很多同学就是学不会或者不想学数学，所以才去考文史的。如果你要不是这类同学的话，考数学还是不错的。

然后，开始划重点啦！！！

第一章：函数、极限与连续

1.求分段函数的复合函数;

2.求极限或已知极限确定原式中的常数;

3.讨论函数的连续性，判断间断点的类型;

4.无穷小阶的比较;

5.讨论连续函数在给定区间上零点的个数，或确定方程在给定区间上有无实根。

这一部分更多的会以选择题，填空题，或者作为构成大题的一个部件来考核，复习的关键是要对这些概念有本质的理解，在此基础上找习题强化。

第二章：一元函数微分学

1.求给定函数的导数与微分(包括高阶导数)，隐函数和由参数方程所确定的函数求导，特别是分段函数和带有绝对值的函数可导性的讨论;

2.利用洛必达法则求不定式极限;

3.讨论函数极值，方程的根，证明函数不等式;

4.利用罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒中值定理证明有关命题，如“证明在开区间内至少存在一点满足……”，此类问题证明经常需要构造辅助函数;

5.利用导数研究函数性态和描绘函数图形，求曲线渐近线。

第三章：一元函数积分学

1.计算题：计算不定积分、定积分及广义积分;

2.关于变上限积分的题：如求导、求极限等;

3.有关积分中值定理和积分性质的证明题;

4.定积分应用题：计算面积，旋转体体积等;

第四章：常微分方程

1.求典型类型的一阶微分方程的通解或特解：这类问题首先是判别方程类型，当然，有些方程不直接属于我们学过的类型，此时常用的方法是将x与y对调或作适当的变量代换，把原方程化为我们学过的类型;

2.求解可降阶方程;

3.求线性常系数齐次和非齐次方程的特解或通解;

4.根据实际问题或给定的条件建立微分方程并求解;

综合题，常见的是以下内容的综合：变上限定积分

第五章：无穷级数

1.判定数项级数的收敛、发散、绝对收敛、条件收敛;

2.求幂级数的收敛半径，收敛域;

3.求幂级数的和函数或求数项级数的和;

4.将函数展开为幂级数(包括写出收敛域);

第六章：空间解析几何和向量代数

1.计算题：求向量的数量积，向量积及混合积;

2.求直线方程，平面方程;

3.判定平面与直线间平行、垂直的关系，求夹角;

这一部分难度在数学中应该是相对简单的，找辅导书上的习题练习，需要做到快速正确的求解。

当然啦，要是需要学习资料的话也可以在下面评论哦~语数英我都有！