探索性因子分析与

验证性因子分析的异同

因子分析旨在通过少数几个潜变量（因子）解释观测题项间的相关性，被广泛应用于探索或检验量表的结构效度。根据是否具备理论基础，可以将因子分析分为探索性因子分析(Exploratory Factor Analysis, EFA)与验证性因子分析(Confirmatory Factor Analysis, CFA)。本文首先概述EFA与CFA在分析目标、统计原理以及基本假设方面的相似之处，再详细探讨EFA与CFA在理论依据、统计原理以及模型设定上的区别，旨在为读者提供清晰的理解和应用指导。

01

EFA与CFA的共同点

1.1 分析目标

因子分析是一种处理连续观测指标与连续潜变量之间关系的测量模型(Measurement Model)，主要目的是解释观测指标之间的相关性和简化数据。

第一，因子分析旨在发现能够解释观测指标间共同部分的公共因子。一旦这些潜在的公共因子被提取出来，观测指标间的相关性将不复存在，从而实现局部独立。

第二，通过将大量观测指标归纳为少数几个公共因子，因子分析简化了数据结构，便于后续变量关系的检验。

在学术研究中，抽象概念虽不直接存在于真实世界中，但可通过具体的观测指标间接反映。因子分析的作用在于，它能够将大量的观测指标简化为能够反映指标间共同成分的少数几个因子，而这些潜在因子便是相应抽象概念的表征。

1.2 统计原理

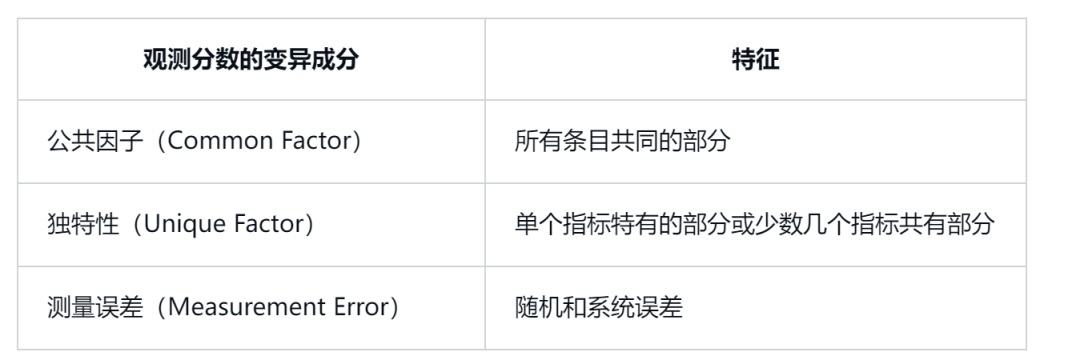
在统计原理上，因子分析将个体在观测题项上的分数变异分解为公共因子(Common Factor)、独特性(Unique Factor)、以及测量误差(Measurement Error）三个部分，详见下表。然而，在统计软件的设定中，独特性与测量误差往往被合并为误差项。

Example

探索性因子分析：

验证性因子分析：

x为观测变量，F为公共因子，ε为独特性与测量误差的合并项

1.3 基本假设

因子分析建立在四个基本假设之上，这些假设与统计分析中的模型设定紧密相关。

02

EFA与CFA的区别

探索性因子分析与验证性因子分析的区别总结于下表。

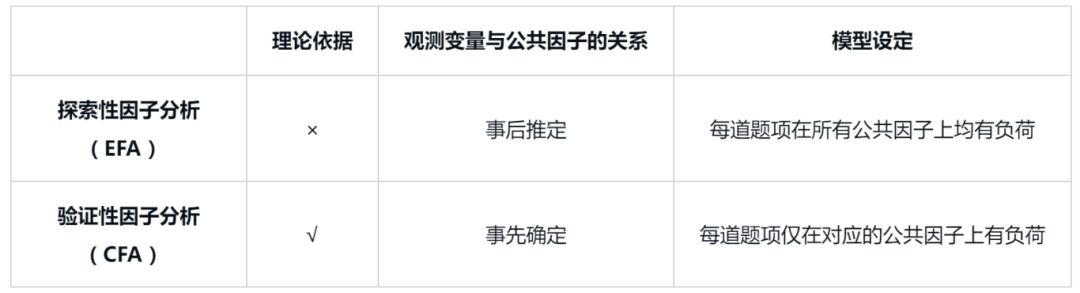
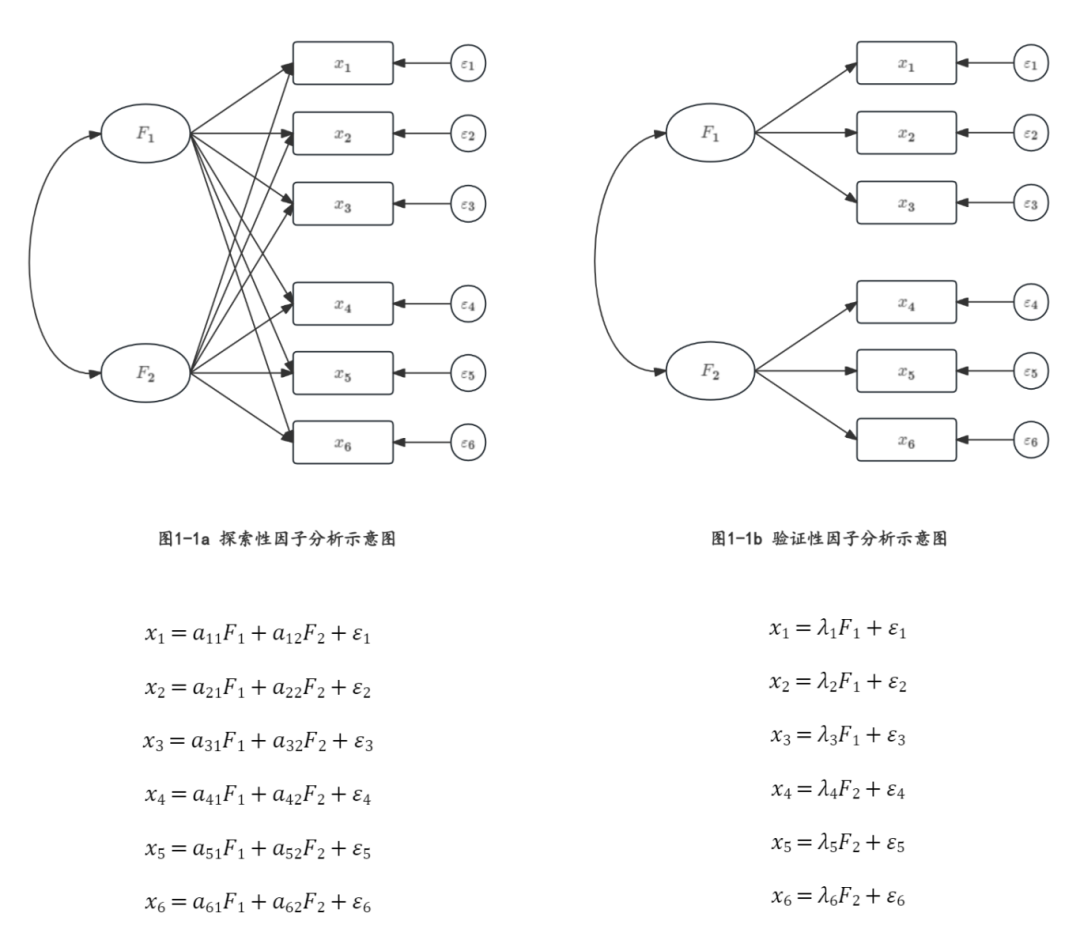
探索性因子分析(EFA)主要用于在无理论依据的前提下，初步探索量表的结构效度。由于缺乏理论指导，EFA不预设观测指标与公共因子(潜变量)之间的隶属关系,而是在分析过程结束后确定这些关系。因此，在模型设定中，假定每道题项在所有公共因子上均有负荷(见图1-1a)。

相反，验证性因子分析(CFA)依据已有的理论基础来验证量表的结构效度。由于具备理论基础，CFA在分析前就明确了观测指标与公共因子(潜变量)之间的隶属关系。因此，在模型设定中，假定每道题项仅在与其对应的公共因子上有负荷(见图1-1b)。

注：

a.椭圆形代表潜变量(F1-F2为公共因子，ε1-ε6为题项独特性与测量误差合并后的误差项)，矩形代表观测变量，双箭头代表公共因子之间的相关，单箭头代表公共因子/误差项对观测变量的预测；

b.探索性因子分析与验证性因子分析均假定公共因子(作为自变量)预测观测变量(作为因变量)；

c.两个测量方程均没有截距项，当x为观测题项的标准化得分时，a/λ代表的是标准化因子载荷；

d.由于CFA不允许存在指标跨负荷，这通常会令因子间的相关虚高(Marsh et al., 2009）

应用成熟量表：通过CFA检验量表的结构效度即可

自编量表：先使用EFA初步确定因子的个数、指标与因子间的关系，再根据EFA的结果在新样本中进行CFA验证(Gerbing & Hamilton,1996)

改编成熟量表：若调查题目增删较多、调查对象跨文化(国外 -> 国内)、或者调查内容跨情境(工作 -> 学习)，可能也需要考虑联合运用EFA和CFA来共同检验量表的结构效度。

03

总结

综上所述，EFA与CFA均旨在将大量的观测指标简化为，能够反映指标间共同成分的少数几个潜在公共因子。但是两类方法在是否有理论依据、观测变量与公共因子之间的关系，以及模型设定上存在着较大区别。