盒形图（Box Plot）包含了丰富的信息！

它展示了：

最小值（Minimum），最大值（Maximum），第一四分位数（1st Quartile），第三四分位数（3rd Quartile）和中位数（Median）。

​

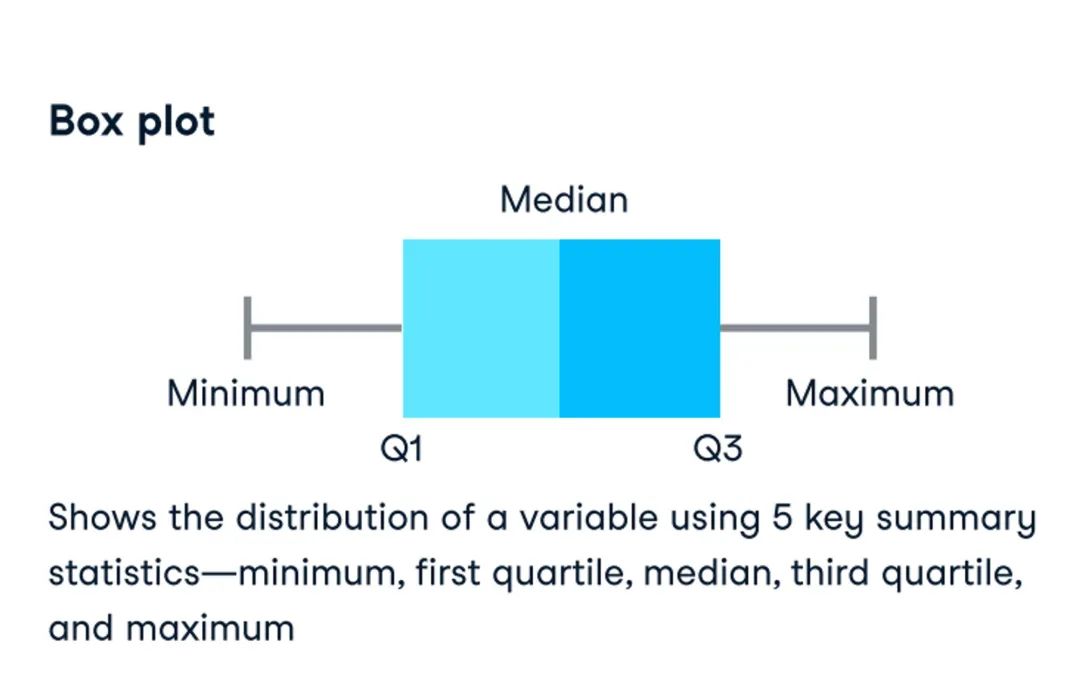
盒形图，也被称为箱线图或箱须图，是展示数据集分布和关键特征的绝佳方式。

它们提供了一个清晰且简洁的总结，包括：

> 中心趋势（Central tendency）

> 数据分散度（Spread）

> 异常值（Outliers）

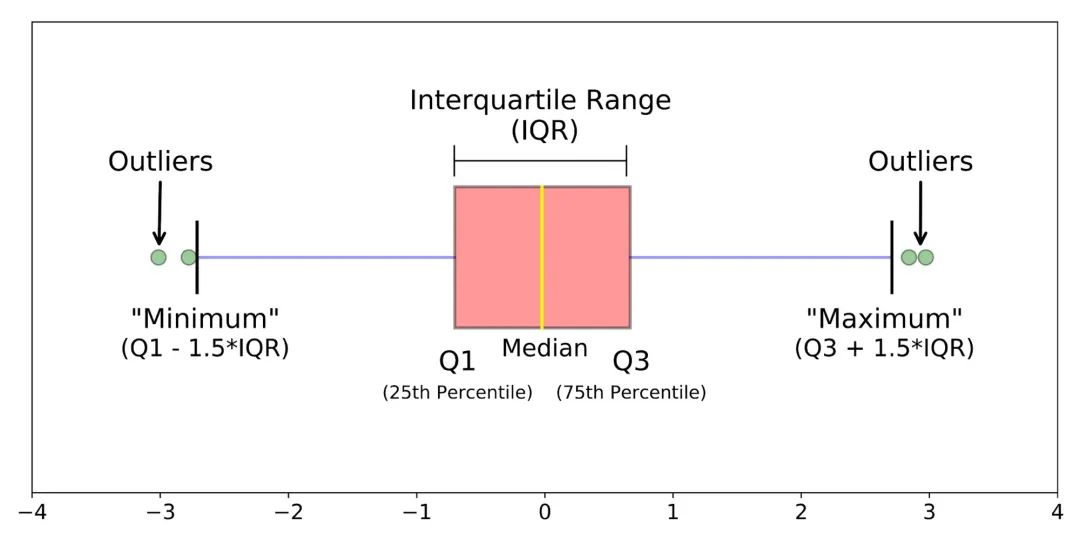
盒形图中的盒子代表了四分位数范围（interquartile range，IQR），包含了中间50%的数据。

盒子里的线代表了中位数（median），将数据分成了两个相等的部分。

盒形图的须（whiskers）从盒子延伸出来，代表了数据的变异性。

它们通常延伸至最小和最大的非异常值观测值。

作为个别点或符号显示的异常值（Outliers）位于须之外，突显了极端值。

​

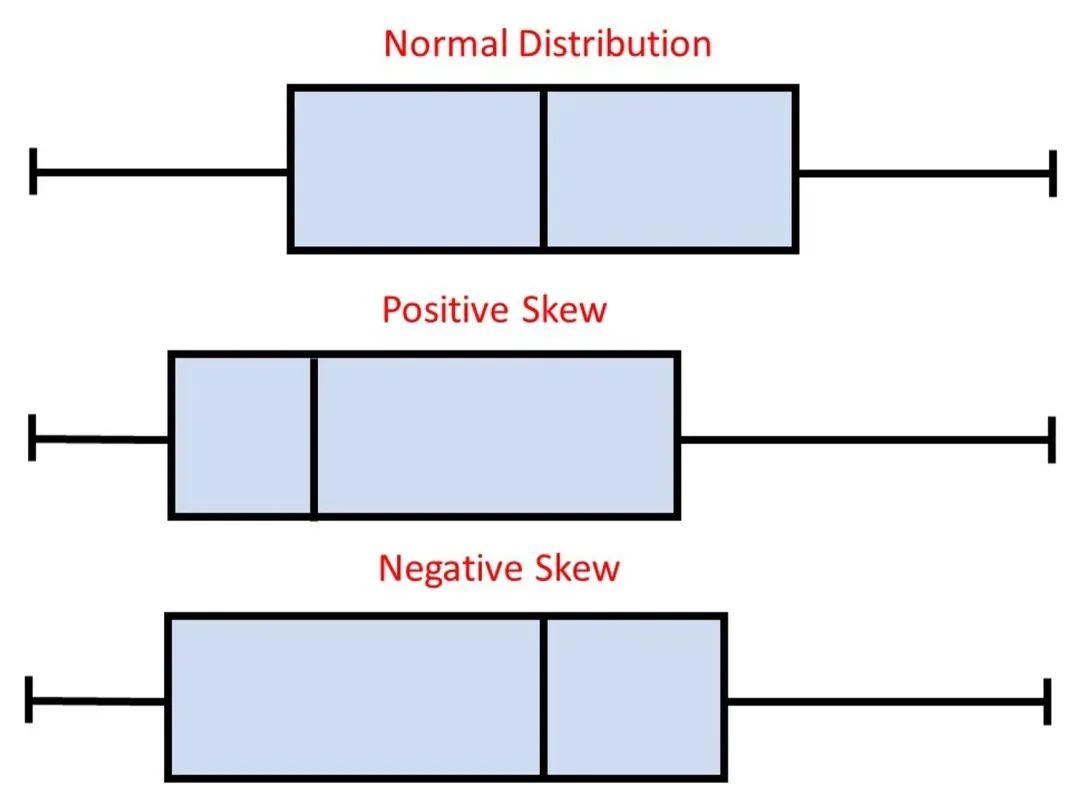
盒形图还可以提供数据分布的对称性或偏态的洞见。

如果中位数不在盒子的中心，它暗示了偏向较长须的偏态。

这有助于我们检测偏离对称分布的情况。

​

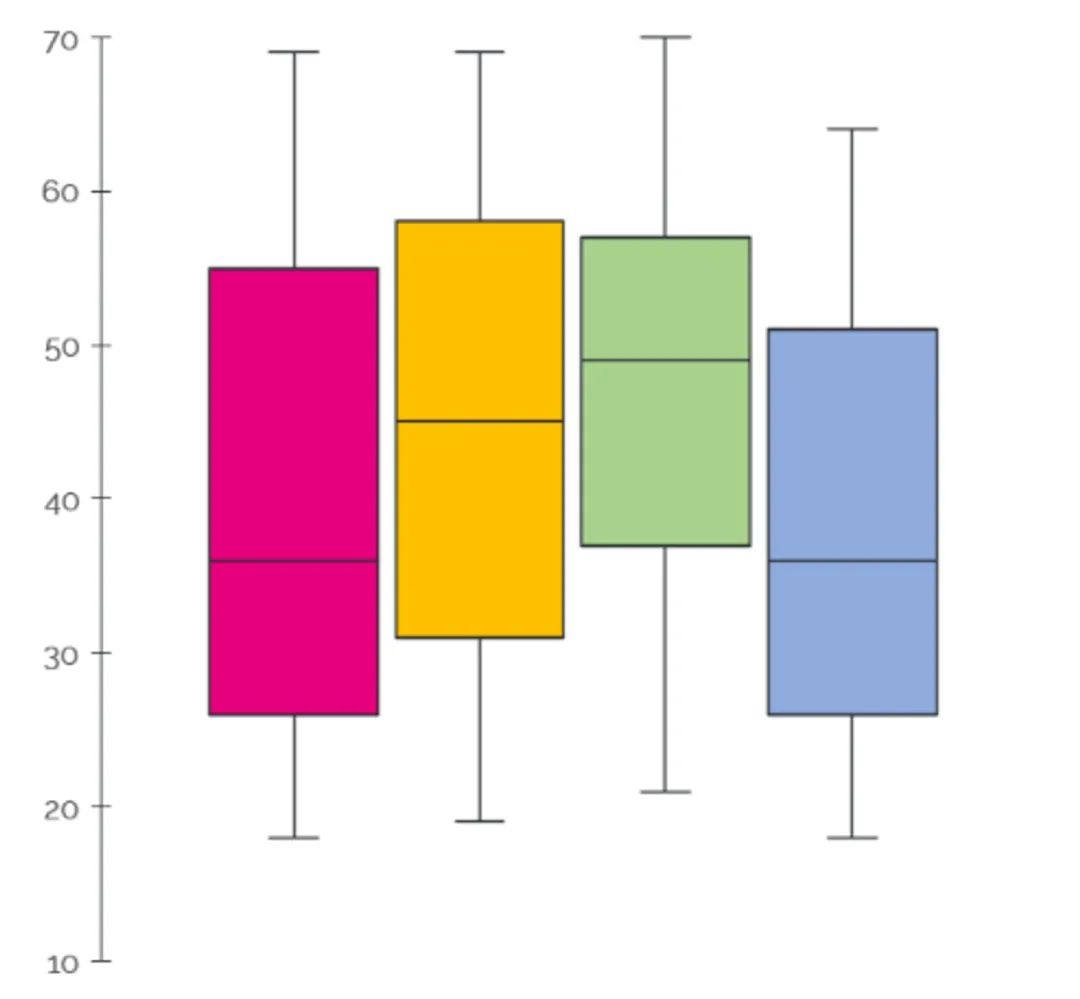
盒形图的另一个宝贵方面是它们比较分布的能力。

我们可以创建并排的盒形图来比较多个数据集，使得识别中位数、分散度和异常值的差异变得容易。

它非常适合于探索性数据分析！

​

什么时候使用盒形图？

它们在总结数据时非常有效，但同时也要考虑上下文。

它还可以描绘出一个特征中异常值的数量。

在比较分布时也非常有用。

盒形图在各个领域得到了广泛应用，包括数据科学、统计学、金融和社会科学。

它们提供了数据分布的快速快照，并为更深入的分析奠定了基础。

案例

盒形图的一个典型案例是比较不同学校学生的考试成绩分布。假设有三所学校，分别为学校A、学校B和学校C，每所学校有一批学生的数学考试成绩。我们想要比较这三所学校学生的数学成绩分布情况，看看哪所学校的学生表现最好，哪所学校的学生成绩最为稳定，以及是否有异常表现的学生。

优点:

1. 数据分布的直观展示: 通过三所学校并排的盒形图，我们可以直观地看到每所学校成绩的中位数，一目了然地比较哪所学校的学生整体表现更好。

2. 数据波动性和离散程度的对比: 盒形图展示了四分位数范围（IQR），让我们能够比较每所学校学生成绩的离散程度。如果某所学校的盒子比其他学校的更短，这意味着该校学生的成绩更为集中，波动性更小。

3. 异常值的识别: 盒形图通过须外的点展示了异常值，帮助我们快速识别出成绩异常高或异常低的学生，为进一步的分析提供线索。

缺点：

1. 数据细节的缺失: 盒形图虽然能够提供数据分布的概览，但它无法显示所有数据点的具体值，也无法展示数据分布的具体形状，如双峰分布或偏斜程度的精确信息。

2. 对大数据集的限制: 在数据点非常多的情况下，盒形图上的异常值点可能会非常密集，使得具体识别每个异常值变得困难。

3. 误解风险: 对于不熟悉盒形图的观众，盒形图的某些元素（如四分位数和异常值）可能会造成误解，需要额外的解释和教育。

总的来说，盒形图展现了其强大的数据可视化能力，能够快速直观地比较中位数、分散度和识别异常值，但同时也需要注意其在数据细节展示和大数据集处理上的局限性。