在介绍尺规作图三大问题的早期历史时，我们曾提到，古希腊几何学家梅内克缪斯（Menaechmus）据信是为了解决“倍立方”问题而提出了圆锥曲线。在他之后，很多其他数学家也对圆锥曲线做了研究，其中包括欧几里得和阿基米德。但圆锥曲线研究的集大成者，则是比阿基米德稍晚的希腊几何学家阿波罗尼奥斯（Apollonius）。

19世纪的版画中展示的阿波罗尼奥斯在亚历山大港演示几何学的场景

阿波罗尼奥斯最重要的著作是《圆锥曲线论》。将3种圆锥曲线命名为椭圆、抛物线、双曲线的做法便出自该书（分别出自第1卷的命题11、12、13）。经过两千多年的时光洗礼，这部总计8卷的著作的第8卷已不幸轶失。存世的7卷中，1～4卷尚有希腊文抄本，5～7卷皆源自阿拉伯文译本。《圆锥曲线论》的整理、翻译、评注者之中，包括了英国著名天文学家爱德蒙·哈雷（Edmond Halley）。哈雷甚至作了很大努力试图恢复第8卷。

与《几何原本》相似，《圆锥曲线论》也以体系见长，不仅成为长时间难以超越的经典，而且也造成了同类著作因无法匹敌而失传。相应地，《圆锥曲线论》的作者阿波罗尼奥斯同样是一位重量级人物。据公元6世纪的希腊数学家欧托修斯（Eutocius)“转发”的公元前1世纪的数学家杰米纽斯（Geminus）的记述，阿波罗尼奥斯被其同时代人称为“大几何学家”；美籍比利时裔科学史学家乔治·萨顿（George Sarton）则称阿波罗尼奥斯为阿基米德之后一个时期里唯一可与阿基米德比肩的几何学家。但阿波罗尼奥斯的知名度—尤其对现代读者来说—却远逊于欧几里得和阿基米德，我们对其生平的了解也相当贫乏。而且因知名度的逊色，后人对阿波罗尼奥斯的记述也很少。不过幸运的是，《圆锥曲线论》所含的几篇书信形式的序言在这方面稍有弥补作用，为我们了解阿波罗尼奥斯的生平提供了一些线索。

9世纪阿拉伯文《圆锥曲线论》抄本

据希腊数学史专家托马斯·希斯（Thomas Heath）介绍，《圆锥曲线论》的序言曾被德国语言学家乌尔里希·冯·维拉莫维茨-默伦多夫（Ulrichvon Wilamowitz-Moellendorff）列为古典希腊文的优美风格之典范。既如此，我们就摘译几段吧—这同时也是对全书内容的一个简介，至于“古典希腊文的优美风格”，在转译下自是无存，就不奢想了。

阿波罗尼奥斯问候欧德摩斯：

……我和你在帕加马相聚的时候，我注意到你热切地想要了解我在圆锥曲线方面的工作，因此我将修订过的第1卷寄给你。其余各卷一旦修订到令我满意的程度后，也会寄给你的。你肯定尚未忘记我告诉过你的，即我对这一课题的研究是几何学家纳格拉底来亚历山大港，与我在一起时，应他的要求而做的。当我将这一研究写成了8卷书之后，因他即将扬帆远行，我过于匆忙地全数交给了他。因此，那些书并未彻底修订过……也因此，我现在陆续将修订完的部分发布出来……

在8卷书之中，前4卷构成了一个初等介绍。第1卷包含了产生3种圆锥曲线及（双曲线的）反向分支的方式，及其所蕴含的基本性质，阐述得比他人的著作更完整和普遍。第2卷包含了圆锥曲线的直径、轴以及渐近线的性质……你可以从这卷中了解到我所说的直径和轴的各自含义。第3卷包含了很多有关轨迹和交点的精彩而有用的定理，这些定理中最漂亮的是新的，它们的发现使我意识到欧几里得并未解决相对于三条和四条直线的轨迹问题……因为缺了我所发现的新定理的辅助，那是不可能解决的。第4卷展示了圆锥曲线相互之间以及与圆周之间的相交可以有多少种方式，以及其他一些附加话题，这些在我之前全都没人讨论过……

其余各卷多为题外话：其中一卷比较全面地处理了极大和极小，另一卷是关于圆锥曲线的全等和相似，还有一卷给出了一些旨在确定极限的定理，最后一卷是关于确定圆锥问题。当然，等到所有各卷都发表之后，所有阅读这些书的人都可依照自己的口味，形成他们自己的判断。

以上是第1卷序言的主要部分。这篇序言是写给帕加马王国的一位名叫欧德摩斯（Eudemus）的教师的，虽只是第1卷的序言，却对全书作了总括。

《圆锥曲线论》第2卷的序言非常简略，只是说派儿子将该卷带给欧德摩斯，让后者与热爱这一课题的学生—尤其是菲洛尼底斯（Philonides）—分享。但尽管简略，这篇序言对了解阿波罗尼奥斯的生平却有不小的作用，因为其中提到的欧德摩斯的学生菲洛尼底斯被认为生于公元前200年，卒于公元前130年，且欧德摩斯是他的第一位老师。由此推断，这篇序言的撰写当在公元前2世纪的早期，此时阿波罗尼奥斯已有一个能替他送书的儿子，起码应是中年，学术生涯的活跃期则可推测为从公元前3世纪后期到公元前2世纪早期。

《圆锥曲线论》的第3卷没有序言，第4卷的序言则是写给一位名叫阿塔罗斯（Attalus）的人的。这位阿塔罗斯被认为很可能是帕加马国王阿塔罗斯一世（King Attalus I）—此人的统治时间是公元前3世纪后期到公元前2世纪初，与阿波罗尼奥斯学术生涯的活跃期重叠。下面摘译一些第4卷序言的片断。

阿波罗尼奥斯问候阿塔罗斯：

一段时间以前，我将自己有关圆锥曲线的8卷书中的前3卷寄给了欧德摩斯并作了说明。但由于他已去世，而您对拥有我的著作怀有热诚，我决定将余下几卷献给您。我这次寄给您的是第4卷……所有那些未曾在其他地方见过的内容，都需要用很多类型各异的新奇定理来解决，那些定理中的绝大多数我其实已在前3卷里给出了，其余则收录在本卷。这些定理对综合问题及交点问题都有很大用处……哪怕不考虑这种用处，仅仅出于展示其本身之故，它们也该被认为是值得接受的，就像我们也会仅仅出于这一原因而接受数学中的很多其他东西。

译文中的两处省略，一处是对第4卷内容的介绍—跟第1卷序言里的介绍相似，只是更详细些；另一处则是对前人工作的评述，大意是说前人虽做过一些工作，却不能令人满意。虽然第1卷和第4卷的序言都提到了对前人的超越，但一般认为，《圆锥曲线论》的前4卷有很大比例是承自前人—尤其是欧几里得和阿基米德。

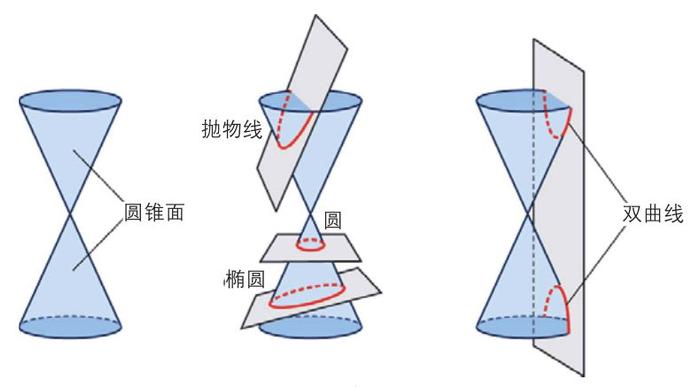
圆锥曲线是由平面通过不同角度与圆锥面相交得到的二维曲线，包括了椭圆（包括圆）、抛物线和双曲线，即阿波罗尼奥斯所谓的“3种圆锥曲线及（双曲线的）反向分支”。

《圆锥曲线论》其余几卷的序言也是写给阿塔罗斯的，其中第5卷的序言提到“确立了与最长和最短直线有关的命题”，并宣称有很高的原创度。这里所谓的“最长和最短直线”是指从不在圆锥曲线上的任意一点到圆锥曲线的最长或最短线段。第1卷序言里，针对“其余各卷”所提到的“其中一卷比较全面地处理了极大和极小”，指的就是第5卷对“最长和最短直线”的讨论。

第6卷和第7卷的序言都比较简单，分别对应于第1卷序言里针对“其余各卷”所提到的“另一卷是关于圆锥曲线的全等和相似”及“还有一卷给出了一些旨在确定极限的定理”。其中第7卷的序言表示“这一卷包含了关于直径及在直径之上构筑出的图形的很多新命题。所有这些命题都在很多类型的问题中有应用，尤其是在确定它们的可能极限方面”，对第1卷序言里含糊不清的“旨在确定极限的定理”稍有澄清作用—但所谓“极限”到底是什么，仍未明示，不过第7卷正文里的一些关于直径和轴的不等式可理解为确定了某种变化的界限，似为“极限”之意。第7卷的序言还特意提到了“第8卷……将要讨论并证明的有关圆锥曲线的问题中，有一类是很需要这些命题的”，从而在7、8两卷之间建立了关联，哈雷试图恢复第8卷的努力就在很大程度上基于这种关联。

关于阿波罗尼奥斯的《圆锥曲线论》就介绍到这里。对现代读者来说，这部著作早已不是学习圆锥曲线的有效读物了，解析几何、射影几何等的崛起为圆锥曲线提供了简单、强大并且深刻得多的表述工具。用萨顿的话说，“现在还通过阿波罗尼奥斯来学习圆锥曲线将是愚蠢的”。在这点上《圆锥曲线论》明显逊色于《几何原本》，阿波罗尼奥斯的知名度之远逊，很大程度上也是因为这个—当然，跟题材的专门性也不无关系。

但《圆锥曲线论》的影响却是深远的。后世的知名数学家如吉拉德·笛沙格（Girard Desargues)、布莱兹·帕斯卡（Blaise Pascal)、皮埃尔·德·费马（Pierre de Fermat)、詹姆斯·格雷果里（James Gregory）等都直接间接地受过它的影响。著名天文学家约翰内斯·开普勒（Johannes Kepler）更是用圆锥曲线奠定了行星运动定律的基础，并为牛顿万有引力定律的发现埋下了伏笔。阿波罗尼奥斯的《圆锥曲线论》虽久已淡出多数人的视野，却完成了很辉煌的历史使命。

本文选自《科学世界》2019年第12期