时间飞快，暑假即将进入尾声，最后的几讲，《暑假特辑》将为你带来更多数学史话，数学故事，让大家在探索发现中，迎接新的学期！

一、前言

首先，我们来看一张明信片．这是中国邮政为了纪念2002年8月，在首都北京举行的第24届国际数学家大会而专门发行的．

在明信片的左下角，出现了“勾股”“弦图”的字样，而在右上角，则是该届国际数学家大会的会标，这两幅图中，有什么联系呢？

其实，会标源自中国古代数学家赵爽为了证明勾股定理的而给出的一种辅助图．后来也被称作“赵爽弦图”，那么到底什么是勾股定理，赵爽又是如何借助他的弦图来证明的呢？

二、概念

勾股定理是一个基本的几何定理，即直角三角形两条直角边的平方和 等于 斜边的平方．

中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理(商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例)．在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派．

勾股定理用代数思想解决了几何问题，也是数形结合的纽带，它是人类早期发现并证明的重要数学定理．（以上摘自《百度百科》）

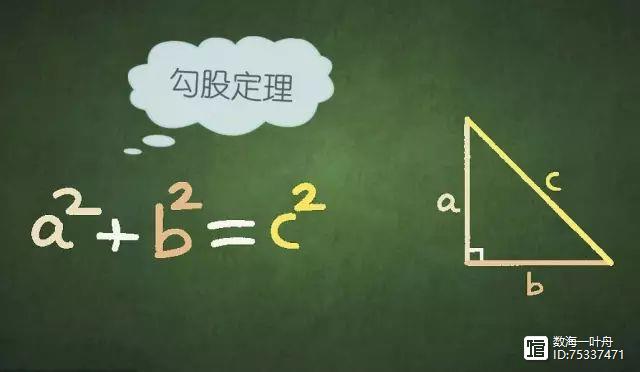
三、证明

现如今，勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一．下面我们一起来看看其中知名度较广的几种有趣证法．

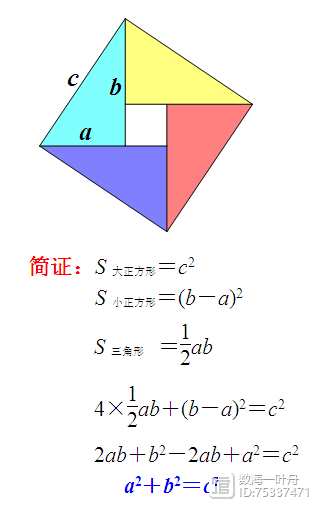
赵爽弦图

(东汉末至三国时代吴国人，我国历史上著名的数学家与天文学家)

邹元治证法

(很遗憾，网上找不到此人生平)

梅文鼎证法

(清朝数学家与天文学家，被世界科技史界誉为与英国牛顿和日本关孝和齐名的“三大世界科学巨擘”)

青朱出入图

(东汉末年数学家刘徽根据“割补术”证明)

欧几里得证法

(出自其作《几何原本》)

给出动态图加以演示：

如果你觉得以上证法还是停留在数学计算的领域，那么我们来个生活中的例子加以检验，来看看这个著名的数学定理是多么美妙！