一

因素分析的基本原理

1.因素分析含义

因素分析是基于相关关系对众多数据进行降维（即简化）的数据处理方法，目的在于挖掘出众多数据后的某种结构。因素分析分为探索性因素分析和验证性因素分析，笔者将重点来介绍探索性因素分析。

探索性因子分析含义：依据样本数据，根据变量间相关性的大小对变量进行分组，每组内的变量之间存在较高相关性，意味着这些变量背后有共同的制约因素，用这些公共因子来代替原始的众多变量的过程。

2.因素分析的条件

（1）所有变量须为连续变量，顺序变量与类别变量不能进行因素分析。

（2）样本量有一定的规模。实际上，对因素分析所需的样本数没有绝对的标准。但现在比较认同的有两个观点：

多数学者认为，受试样本数要比量表题项数多（如一个量表有20个题项，则在因素分析时，样本数要>=20。）

学者Gorsuch（1983）提出，题项与受试者的比例最好为1:5；受试总样本数不得少于100人，若研究主要目的为找出变量群中涵括何种因素，则样本数要尽量大。

（3）变量间的相关程度。因素分析要求变量间有适当的相关性，若相关程度太高，可能会发生多重共线性问题；若相关程度太低（一般绝对值

巴特莱特球形检验（Bartlett-test of sphericity），若其统计量较大且P值

KMO取样适合度检验：

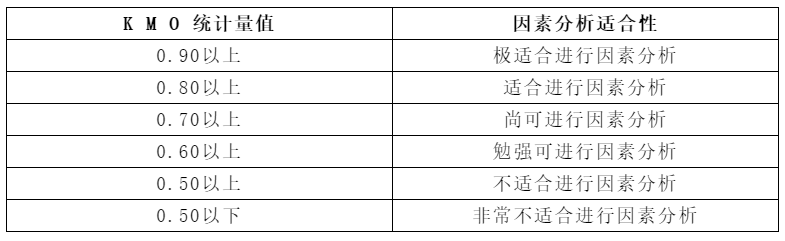
3.筛选题项

若题项间有明显的相关关系，则因素分析会构建成有意义的内容，若一个变量与其它变量相关性很低，在下一个步骤中可以考虑剔除一个变量，但实际排除与否，还要考虑变量的共同性和因素负荷量。若以原始资料做因素分析的数据时，电脑会自动先转化为相关矩阵方式，再进行因素分析。

4.确定公共因子的数量

（1）Kaiser's准则，选取特征值大于1的，这也是SPSS 默认标准。特征值反映了原始变量的总方差在各公共因子上重新分配的结果。特征值越大该公共因子就越重要。

（2）陡坡图检验法（scree plot test），将每个因素依其特征值的大小递减排列，根据陡坡图的形状，提取图中最大拐点前“碎石”的数量。

（3）累积贡献率原则。根据前几个成分累积贡献率达到的百分比来确定公共因子的数量（一般最少为50%以上的累积解释变异量），方差贡献率是指单个公因子引起的变异占总变异的比例，说明此公因子对因变量的影响力大小，贡献率越高说明该因子所代表的原始信息量越大。此方法可以保证较高的累计贡献率，但提取的公共因子的数量一般较多。

（4）若对于业务非常了解，可以事前定好因素数目。

5. 选择抽取共同因素的方法

（1）提取因子的方法有七种：

主成分分析法、主轴法、一般化最小平方法、未加权最小平方法、最大概似法、Alpha因素抽取法、映象因素抽取法。

（2）如何选取？

一是考虑因子分析的目的，二是对变量方差的了解程度。具体来说，如果因子分析的目的是用最少的因子最大程度解释原始数据的方差,则应用主成分分析法，主成分分析法（PFA）为最常用的方法;若因子分析的主要目的是确定数据结构,则适合用主轴因子法，因为主轴因子法符合理论要求，不过，二者的结果通常一致。

ps：主成分是以全体变异量为分析对象，主轴因素法是以变量间的共同变异量为分析对象。

6. 因素旋转

因素旋转后因子载荷将得到重新分配，因子载荷的差异变大，使得因素负荷量易于解释。

（1）常用方法：

最大变异法（Varimax）、四次方最大值法（Quartimax）、相等最大值法（Equamax）、直接斜交转轴法（Direct Oblimin）、Promax转轴法。前三种属于正交转轴法，即因素与因素间没有关联；后两者为斜交转轴法，表示因素与因素间有某种程度的相关。若为正交旋转，以旋转后因素负荷量矩阵为准；斜交旋转，建议以模式矩阵（即因素对项目的加权系数）为准。

（2）优缺点：

正交旋转能容易地解释和表示因子分析的结果，但有些因子可能不一定完全无关，违背了实际情况，与实际不符。斜交旋转则更接近实际情况，符合现实，但研究者必须探测出各因子确切的相关系数，确定斜交旋转的参数。

7. 公共因子的命名

根据因素负荷量将项目归类，参考因素负荷量绝对值>30的项目，认真思考总结各个因子下原始变量的共同特征，对因素加以命名。

因素分析操作步骤

因素分析是spss中一个重要的功能，他的作用是从多个变量中提取少数几个因子，达到减少指标的目的；有时候因素分析方法用在问卷编制中，可以从各个题项中提取中几个维度。

下图看到就是我们要分析的数据，进行因素分析。

Step1：在菜单栏上执行：[分析]—[降维]—[因子]，打开了因素分析对话框.

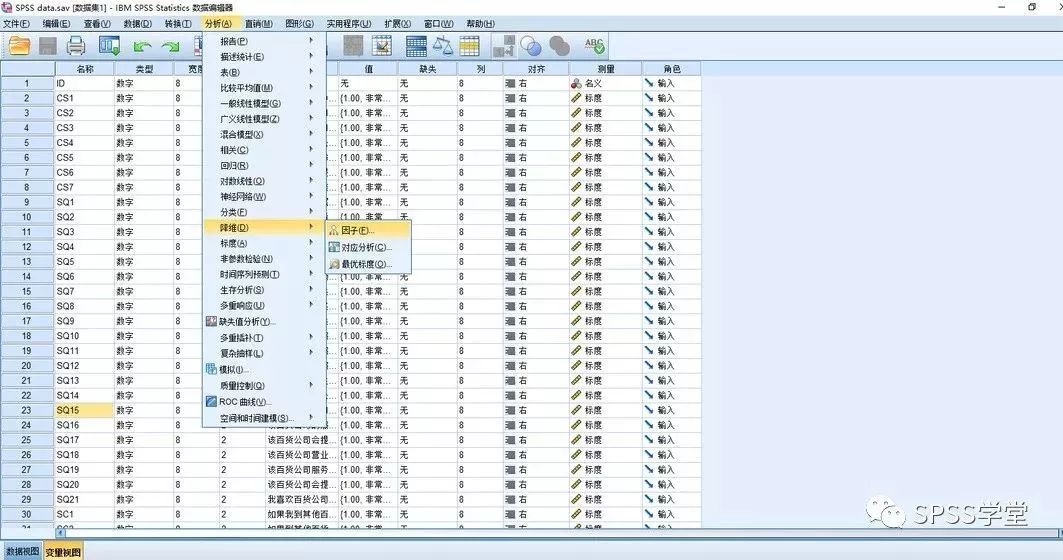
Step2：打开了因素分析对话框，将要分析的这变量放到[变量]框中，点击箭头按钮就可以添加变量。

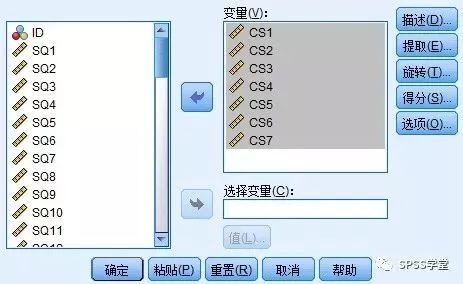
Step3：还是在因素分析的主对话框，点击【描述】按钮，打开描述统计的子对话框。在子对话框中，我们需要对因素分析是否合适进行检验，勾选如图所示的选项，点击【继续】返回到主对话框。

Step4：然后在主对话框中，点击【提取】按钮，打开子对话框。

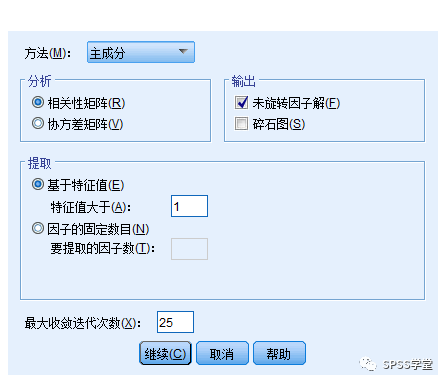
Step5：再在主对话框中，点击【旋转】按钮，打开子对话框，勾选如图所示的选项，点击【继续】返回到主对话框。

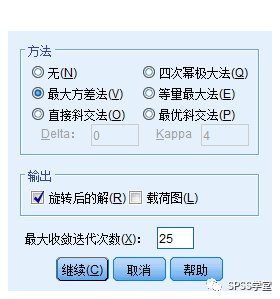
备注：如果使用者根据理论基础或文献探讨，认为因子之间没有相关，就采用正交/直接转轴法，正交转轴法中最常使用为最大变异法。如果因子之间有相关性，就应采用斜交转轴法，斜交转轴法中较常使用者为直接斜交法和或最优斜交法。在进行因素分析时最常用的方法是最大方差法。

Step6：在主对话框中，点击ok按钮，开始处理数据并输出结果

因素分析的结果解读

前面我们已经介绍了因素分析的基本原理和操作步骤，本部分介绍如何解读因素分析的结果。

举个栗子：现在要对30个省、自治区的经济发展状况进行排序，经济发展状况可通过6个指标进行衡量，分别是①GDP ②居民消费水平 ③固定资产投资 ④职工平均工资 ⑤商品价格指数 ⑥工业总产值。可得这是一个综合评价问题，各指标间存在数值关联，且各指标重要性也有所差异，因此我们通过因子分析找出能综合主要信息的少数几个随机变量并对其进行排序分析。

依次选择【分析】--【降维】--【因子分析】打开因子分析主对话框；

选择【描述】-【系数】和【KMO和Bartlett球形检验】回到主对话框；

选择【抽取】-【相关性矩阵】和【碎石图】回到主对话框；

选择【旋转】-【最大方差法】和【旋转解】回到主对话框；

选择【得分】-【保存为变量】【回归法】和【显示因子得分系数矩阵】回到主对话框；

选择【选项】-【按大小排序】和【取消小系数】回到主对话框；

在主对话框点击【确定】，分析结果及解读如下：

因素分析结果解读

1、图1 为六个原始变量之间的系数矩阵，可见变量之间确实存在一定的相关性，存在信息的重叠，进行因子分析有一定的必要性。

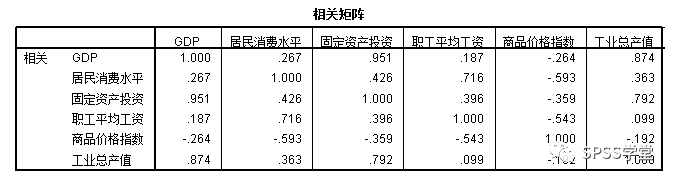
图1

2、图2为KMO和Bartlett球形检验结果，Bartlett检验表明，sig.为0.000，拒绝各变量独立的假设。KMO检验变量间的偏相关是否较大，KMO值大于0.7代表因子分析效果较好，小于0.5则表明不适合运用因子分析，此题KMO值为0.583，说明各变量间信息重叠程度不是特别高，可以尝试进行因子分析。

图2

3、图3给出公因子方差，表示原来六个变量中所含原始信息被提取的公因子所表示的程度，提取程度表明公因子对各变量的解释能力是较强的。

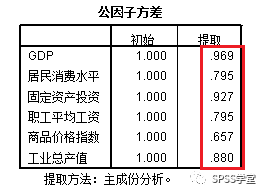
图3

4、图4为各成分的方差贡献率和累计贡献率，只有前两个主成分的特征根大于1，SPSS默认提取前两个主成分，前两个主成分的累计方差贡献率为83.730%，因此，选择前两个主成分可以对30个省市、自治区的经济发展状况进行描述和排序。

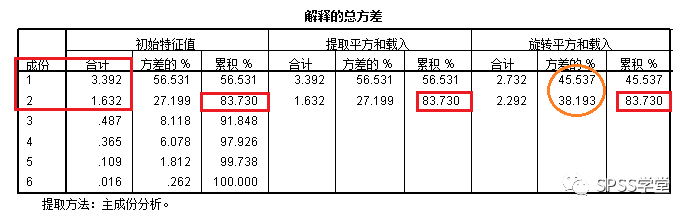
图4

5、图5为碎石图，可以帮助我们判断各因子的重要程度，纵轴为特征根大小，横轴为因子序号，由图可见前两个因子位于陡坡，作用明显，后四个因子形成平台，特征根小于1，作用较弱，因此考虑前两个公因子即可。

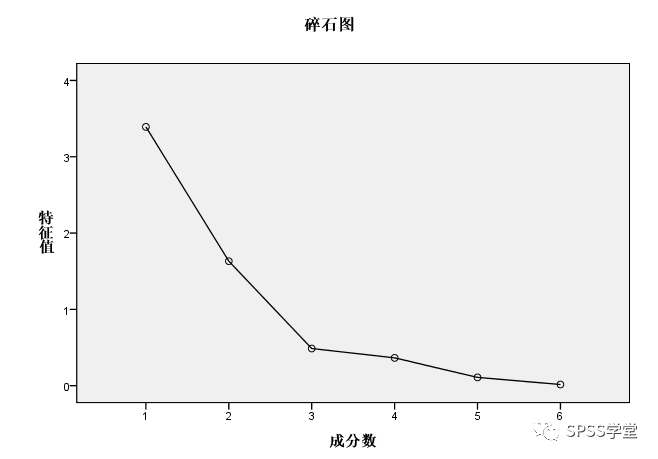
图5

6、图6为成份矩阵表，反映各因子在六个变量上的载荷，各因子对各变量的影响度依次为：

Zx1=0.844F1+0.507F2+ε1

Zx2=0.706F1-0.545F2+ε2

Zx3=0.913F1+0.306F2+ε3

Zx4=0.598F1-0.661F2+ε4

Zx5=-0.604F1+0.540F2+ε5

Zx6=0.791F1+0.505F2+ε6

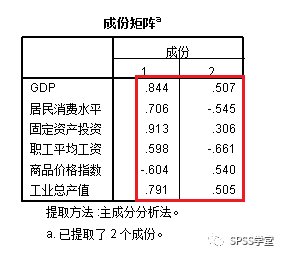
图6

7、图7为旋转成分矩阵。因子旋转是通过改变坐标轴位置，重新分配各个因子所解释的方差比例，使其载荷系数更接近1或0，能更好地解释和命名变量。旋转后的因子不改变模型对数据的拟合程度，也不改变各个变量的公因子方差，使因子结构变得更简单。由旋转成分矩阵可以看出，第一个公因子（Factor1）主要从GDP、工业总产值和固定资产投资来反映经济发展状况，可将其命名为总量因子；第二个公因子（Factor2）主要从职工平均工资、居民消费水平和商品价格指数来反映经济发展状况，可将其命名为消费因子。

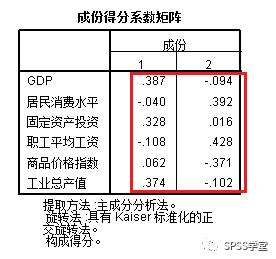
图7

8、图8为成份得分系数矩阵。据此得出各公因子的表达式为：

F1=0.387Zx1 - 0.040Zx2 + 0.328Zx3 - 0.108Zx4 + 0.062Zx5 + 0.374Zx6

F2=-0.094Zx1 - 0.392Zx2 + 0.016Zx3 - 0.428Zx4 - 0.371Zx5 - 0.102Zx6

图8

9、依次选择【转换】-【计算变量】,考虑各公因子对应的方差贡献率比例为权数计算综合得分（见图4），生成一个新变量“Score”，代表各地经济发展状况的总体水平，如图9所示。再将“Score”进行降序排列，如图10所示。可得到30个省、自治区的经济发展情况排序，经济发展状况的前五名如图11所示。可以看到广东综合得分最高，排名第二的上海主要依靠消费因子在拉动经济水平，排名三四的江苏、山东则主要依靠总量因子拉动，各个因子有明确的含义，综合比较结果可以很好的解释各地区整体经济发展的优点和劣势，有利于各区域有针对性的确定发展方向和目标。

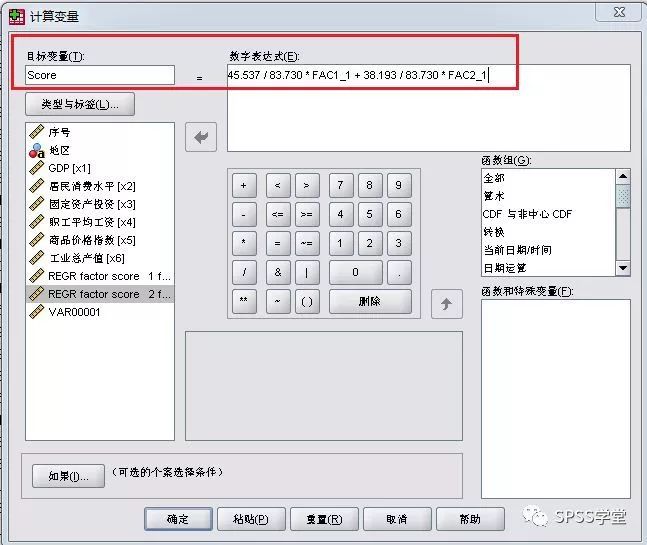
图9

图10

图11

注：本文授权转载自SPSS学堂，感谢作者Jingle、红豆牛奶、晃晃悠悠。