摘要:社会舆论的形成是个体行为及其关联与社会环境影响共同作用的结果. 在受到环境因素影响的同时, 个体行为也反过来影响社会环境, 从而呈现出耦合演化的特点. 本文在Ising模型的基础上, 建立了一个包含社会张力累积和消解过程的舆论形成模型, 研究了个体行为和社会环境的耦合演化行为. 利用朗道的平均场理论, 重点分析了在不同舆论疏解系数下系统演化的定态解及其稳定性, 以及系统定态解随参数变化的分支行为. 同时使用计算机模拟方法对平均场理论的结果进行了印证. 研究结果表明, 将系统与环境的耦合演化机制加入Ising模型后, 系统会展现出一定的自组织特性. 当疏解系数较小时, 系统会出现不同程度上的整体一致舆论, 产生宏观有序状态; 当疏解系数较大时, 系统则稳定在无序状态. 同时, 存在一个临界参数, 使系统从任何初始状态出发均自发演化到临界的分支点状态.

关键词:/

English Abstract

Opinion formation model with co-evolution of individual behavior and social environmentLiu Xiao-Hang1,

Wang Yi-Ning1,

Qu Zi-Min1,

Di Zeng-Ru2

1.School of Governance, Beijing Normal University, Beijing 100875, China

2.School of Systems Science, Beijing Normal University, Beijing 100875, China

Corresponding author:Di Zeng-Ru, zdi@bnu.edu.cnFund Project:Project supported by the National Natural Science Foundation of China (Grant Nos. 71731002, 61573065) and the National Key Research and Development Plan, China (Grant No. 2017YFC0804000).

Received Date:23 December 2018

Accepted Date:20 March 2019

Available Online:01 June 2019

Published Online:05 June 2019

Abstract:Entering the information era, the formation of public opinion is largely associated with the complex system constructed by the Internet, thereby possessing new characteristics。 The formation of public opinion is the result of the interaction of individual behavior with social environment。 In reality, the environmental factor and the individual behavior are usually related to each other and co-evolve with time。 Based on the Ising model, in this paper established is an opinion formation model that includes the process of the accumulation and digestion of the social tension。

In the model, a parameter named effective dissolving factor c is designed to represent the extent of the interaction between the system and the social environment。 A two-dimensional dynamical system is involved in the model to describe the dynamics of individual behavior and social tension。 The co-evolution behavior of the system is studied。 Based on the Landau mean field theory, the stationary states of the dynamical system under different parameter values, i。e。 the value of effective dissolving factor c, their stability and bifurcation of the system, are analyzed。

Finally, the computer simulation method is used to verify the results。 The research shows that with the co-evolution mechanism of the system, our model exhibits certain self-organization characteristics。 When the effective dissolving factor c is smaller than the threshold value, the system will reach final consensus opinion, resulting in a macroscopically ordered state。 Otherwise, when the dissolving factor c exceeds a threshold value, the system is stable in the disordered state。 It is interesting to find that there is such a critical value of the parameter that it leads the system to be self-organized into a critical state from any initial state。

The future detailed investigation on the criticality of the co-evolving system is also suggested, such as testing whether the system has evolved into the critical state according to the finite-sized scaling theory and calculating the critical exponent of the system。 In addition, in this paper provided is a new perspective to tackle practical problems in public opinion。 Based on the mechanism of the formation of public opinion revealed by our model, researchers are encouraged to conduct studies on how to monitor the state of public opinion more precisely and to predict the tipping point of the system evolution。

Keywords:/

全文HTML-->-->-->1.引言进入21世纪以来, 信息网络技术的飞速发展, 深刻地改变着社会经济形态, 使得我们的社会成为一个强关联的复杂系统. 社会舆论形成也因此与网络上的信息传播紧密地联系在了一起, 网络社会所特有的实时互动和虚拟性等特点, 使得社会舆论的形成和发展具有了新的特性, 迫切需要我们利用复杂性研究的视角和方法, 认识和理解其中的核心科学问题.

实际上, 对社会舆论形成机制和演化规律的研究早已成为科学探索的一个重要议题. ****们从不同的角度提出了多种舆论动力学模型[]. 其中, 统计物理中的Ising模型, 由于其中自旋粒子向上或向下的两种状态, 可以自然地刻画人们观点的左右区分、或支持与反对的态度, 因而被广泛应用到舆论形成的研究中[]. 在这一类模型中, 研究者将个体抽象为系统中的粒子, 粒子的状态表示个体持有的观点, 定义粒子间的微观交互规则及粒子状态转变规则, 在给定的初始状态分布下, 个体按模型规则进行交互, 推动着宏观舆论的演化, 最终可能演化到所有个体的观点出现统一、极化和分裂现象. 类比于Ising模型对铁磁物质相变的理解, 舆论形成也被描述为通过相变产生有序现象的过程. 在Ising模型的基础上, 研究者们又提出了一系列经典的舆论动力学模型, 例如: 投票者模型[]、多数决定模型[]、Sznajd模型[]、Deffuant模型[]以及Krause-Hegselmann模型[]等. 随着复杂网络研究的兴起, 社会个体之间相互作用的网络结构对舆论形成的影响也成为广受关注的一个重要主题. 人们发现在复杂网络的框架下, 能够更好地理解舆论形成现象[-], 而网络结构和舆论行为的共同演化模型[]、羊群现象与种族分割等的讨论[,], 则更全面地描述了结构和行为的相互关系. 我国许多研究团队也在这一方向上开展了卓有成效的工作. 程洁和狄增如[]研究了舆论形成和网络结构的耦合演化, 并利用社会层次熵描述了最终舆论分布的结果; 罗植等[]研究了网络空间结构对舆论形成的影响; 李振鹏和唐锡晋[-]则利用多主体模型以及数学分析, 深入研究了平衡结构等微观结构性质对舆论形成的影响.

考查已有基于Ising模型的舆论形成模型, 可以发现大部分工作对主体行为的适应性以及系统与环境的相互作用关系刻画不够. 相关研究关注的是系统在一定外界环境下(相当于热力学系统的温度)演化的平衡态, 虽然随后发展的Majority Vote Game等模型已拓展到非平衡系统的定态[-], 但这些模型没有考虑系统状态对环境的反馈影响, 也没有强调个体的适应性行为. 因此, 我们需要改进模型以刻画系统个体行为与环境之间的耦合演化行为, 更好地揭示社会系统舆论形成的机制和演化规律. 实际上, 随着多层耦合网络研究的深入和发展, 通过网络耦合讨论系统协同演化的研究已经越来越受到科研工作者的关注[-].

以经典Ising模型为代表的热力学系统, 热浴所给定的环境温度并不受系统与环境交互的影响. 但社会系统有所不同, 系统中个体的行为不仅受社会环境或氛围的影响, 反过来还会作用于社会, 导致社会整体环境的变化. 具体到舆论形成过程, 个体所组成的社会系统所处的政治、经济、文化等各种环境因素可以用一个社会张力指数来刻画, 它对应于Ising模型中的逆温度参数$ \beta \left( {\beta = \displaystyle\frac{1}{{kT}}} \right)$

, 社会张力指数越大, 人群的非理性和从众行为的倾向越显著, 从而越容易发生舆论的极化行为(类似于Ising的有序相变), 产生舆论的一致性. 同时, 个体的行为, 特别是与舆论相关的现实世界和网络虚拟世界中的集群行为, 会在很大程度上反馈于社会, 影响和改变社会张力指数.

本文建立了一个包含社会张力累积和消解过程的舆论形成模型, 研究个体行为和社会环境的耦合演化行为. 类比于具有自组织临界行为的沙堆模型, 我们将引入社会张力的缓慢增加以及通过舆论集群行为的形成而产生的消解过程, 探讨系统与环境的相互作用关系所导致的系统演化以及有序结构的涌现行为. 在第节中, 我们将首先介绍模型建立的基本思路, 然后在Ising模型平均场理论的基础上, 通过非线性动力学方程来刻画系统演化的自组织行为, 对系统与环境的耦合机制进行模拟分析.

在动力学模型中, 系统仍将依据朗道平均场理论给定的自由能函数, 具有演化到势函数最小的性质, 同时, 我们引入环境逆温度的自积累机制, 以及集群行为对社会张力的疏解机制, 探究不同参数条件下系统演化的稳定状态, 得到系统定态随参数变化的分支图. 我们发现, 当社会疏解等效系数等于1时, 系统从任意给定的初始状态出发, 都会自发演化到临界的分支点状态, 产生类似于沙堆模型的自组织临界演化性质. 在第节中, 我们使用Monte Carlo方法得到了上述机制的数值模拟结果, 与平均场中的分析结果进行互相验证, 并探察系统存在随机性时的演化特征. 第节对研究结果进行了总结和讨论.

2.耦合演化模型及其动力学分析以沙堆模型为代表的自组织临界性理论为理解现实世界中普遍存在的临界现象提供了新的角度[,], 被广泛应用于自然、社会和工程等领域. Brunk认为, 其基本思想同样适用于理解社会. 他基于自组织临界性概念, 提出了社会崩溃理论[,]: 能量缓慢积累; 局部失去稳定性, 累积和雪崩所造成的耗散过程, 共同驱动着系统达到自组织临界态. 显然, 这一过程对于我们正确认识和理解社会舆论的形成机制和演化规律富有指导意义. 在我们的耦合演化模型中, 个体的舆论取向以及个体之间的相互作用仍由Ising模型描述, 模型中节点的自旋方向代表节点的不同态度, 逆温度$ \beta \left( {\beta = \displaystyle\frac{1}{{kT}}} \right)$

就对应于环境的社会张力指数. 但与Ising模型给定β不同, 我们类比于沙堆模型引入社会张力的累积效应和释放过程. 首先, 类似于沙粒的不断增加, 引入一个社会张力指数的累积过程(对应于温度的逐步降低), 同时, 假定系统由于自发涨落或外界刺激而产生一个或几个舆论集团时, 就会释放情绪并通过社会治理导致社会张力指数的疏解(对应于温度的升高). 显然, 在已有的Ising模型的基础上, 社会张力累积和疏解过程之间的竞争将大大丰富模型所能展示的系统演化行为. 下面首先构建基于平均场理论的系统演化动力学模型.

22.1.耦合演化的舆论生成模型 -->2.1.耦合演化的舆论生成模型在模型建立和讨论部分, 为了方便起见, 仍然选取温度T作为模型参数和变量. 由朗道1937年提出的平均场理论, Ising模型在不同温度下的热力学势如所示.

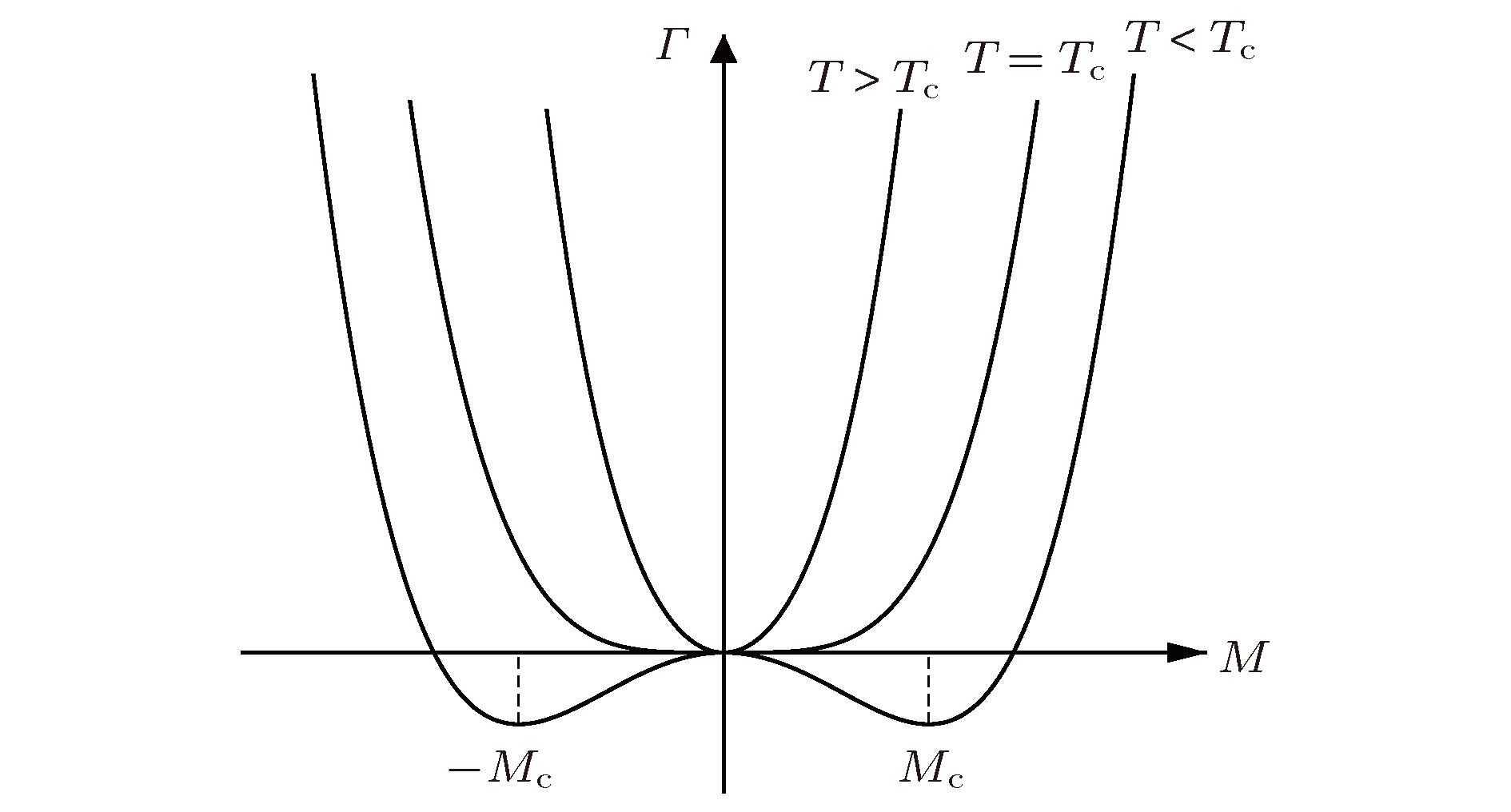
图 1不同温度下的热力学势

Figure1.The Landau potential under different temperatures.

从中可以看到, 当T > Tc时, M0 = 0是稳定的解, 在T = Tc时成为临界点, T < Tc时, M0 = 0解失稳, 出现 ± Mc两个新的非0的稳定解.

考虑一个单轴各向异性的铁磁体系统. 系统的初始温度为T(0), 初始平均磁矩为M(0). 由于势函数Γ的存在, 磁矩随时间的变化可由以下梯度系统描述:

$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = - \nabla \varGamma = - \frac{{\partial \varGamma }}{{\partial M}}.$