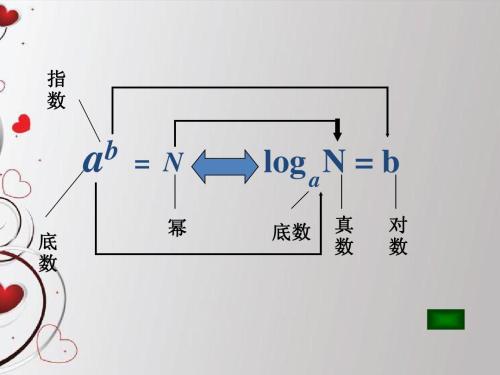
真数和对数的关系：如果a的x次方等于N（a>0，且a不等于1），那么数x叫做以a为底N的对数，记作x=logaN。其中，a叫做对数的底数，N叫做真数。

利用对数，可以把乘、除、乘方、开方分别分为加、减、乘、除。因此，对数能用来简化计算。在16世纪，商业、航海学与天文学得到迅速的发展，为了适应简化复利、天文与球面三角计算的需要，形成了对数的概念。

恩格斯高度评价了对数的作用，把它与解析几何、微积分并称为近代“最重要的数学方法”。由于对数能大大简化计算，历史上曾把它当成计算的法宝，但至今，它的地位已被计算机(器)所取代。

扩展资料：

对数的应用：

1、对数在数学内外有许多应用。这些事件中的一些与尺度不变性的概念有关。例如，鹦鹉螺的壳的每个室是下一个的大致副本，由常数因子缩放。这引起了对数螺旋。Benford关于领先数字分配的定律也可以通过尺度不变性来解释。对数也与自相似性相关。

2、例如，对数算法出现在算法分析中，通过将算法分解为两个类似的较小问题并修补其解决方案来解决问题。自相似几何形状的尺寸，即其部分类似于整体图像的形状也基于对数。对数刻度对于量化与其绝对差异相反的值的相对变化是有用的。

3、此外，由于对数函数log（x）对于大的x而言增长非常缓慢，所以使用对数标度来压缩大规模科学数据。对数也出现在许多科学公式中。