要了解滤波器，我们就不得不深入一下振荡器产生的波形们的真面目。从解构波形的角度出发，我们才会知道：为什么把低通滤波器的截止频率调低，合成器的声音变柔和了，示波器上的波形也磨去了棱角，向正弦波的样子靠近；为什么把滤波器的“共振”调高，合成器的声音又向着“变压器”的声音发展，示波器里的波形开始“扭曲”、“长毛”。如果仅仅是进行“把信号输入、输出连接上滤波器，调调旋钮，声音好听了，去看看下一个模块吧。”这样的简单了解，或许有些人的合成器探索之路会和我最初的状态一样——只知其然不知其因。

百年前，数学大佬傅立叶就提出“任何复杂波形都能分解为一系列不同相位，不同振幅，不同频率的正弦波”。学习过三角函数的我们或许能想到，正弦波的一种绘制方式就是将一个进行圆周运动的点在一条匀速移动纸面上投影。所以从原始信号里分离出的不同正弦波也可以单独理解为一个个始终在旋转圆上的一点。旋转圆的大小决定波的振幅，圆的旋转速度决定波的频率。

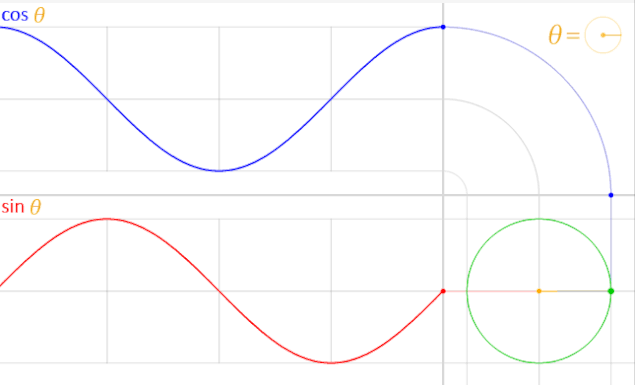
使用旋转圆进行投影的正弦和余弦

现在深入一下，当我们对比起两个同大小，逆时针同转速旋转圆的状态。A圆的点从X轴出发，旋过了90度到达了Y轴上时，B圆的点才从X轴出发。让它们继续旋转一会在纸面上留下投影，这时候两个圆绘出的两道正弦波看起来参差交错，实在想让强迫症们把A和B“攒”在一起。可是如何称呼它们之间的“交错“呢？细细观察波形，它们在一段时间内都有着相同的形状，是不是可以找它们相似的地方来进行对比？是的。既然正弦波的波形在最大和最小值之间规律地来回横跳，我们可以称A正弦波与B正弦波的两个波峰距离为相位，并且它们互有90度的相位差（当然，从波谷或其它地方比对它们间的区别也是可以的，得看选取的点是否方便对比）。以此类推，我们拥有了从0度到360度，对比数个同振幅但不同相位波形不同之处的能力。同时我们也知道了，为什么相位的单位是“度”。

两个振幅相同，但互相偏移90度的正弦波及两者叠加后的波形

那么把它们叠加呢？是不是“峰对峰变大”，“峰抵谷变小”？

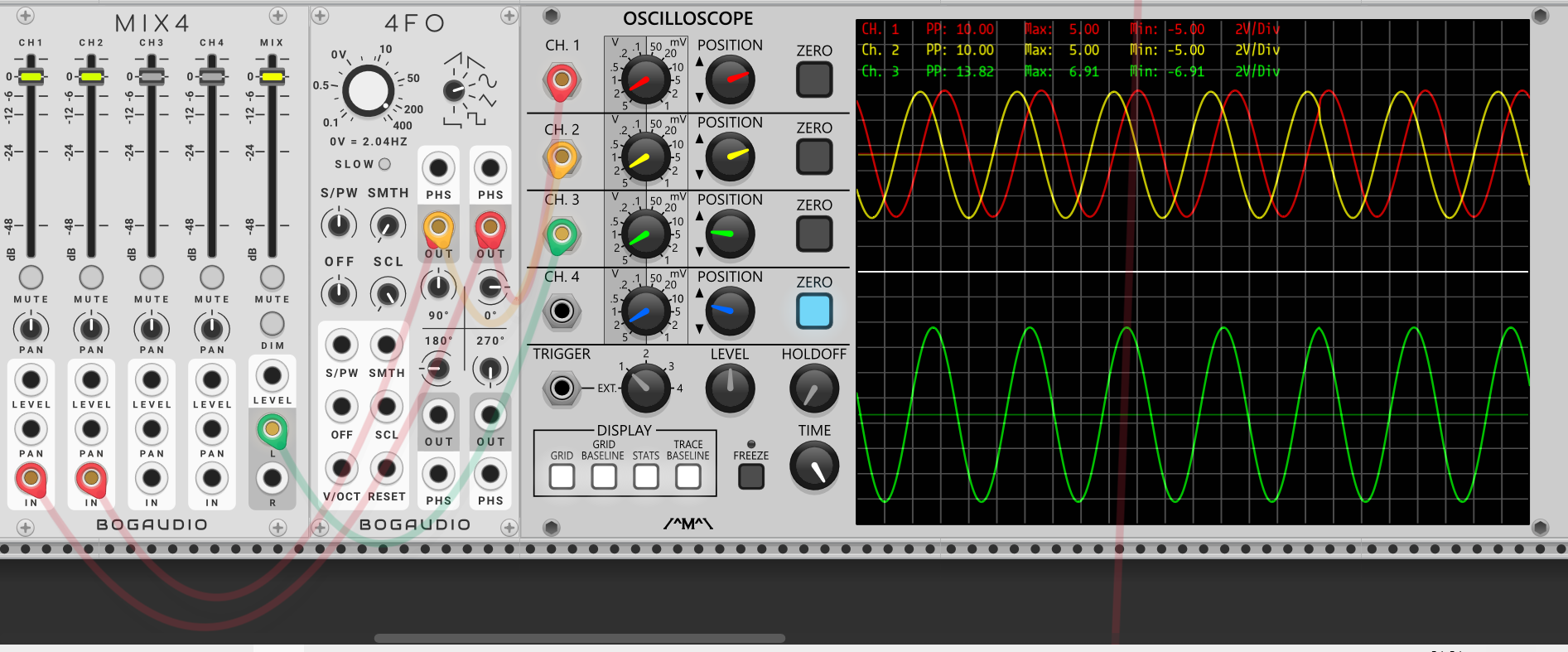
猜对了！就像我使用“Bogaudio”的相位可调低频振荡器“4FO”演示的一样，同相位（两个波形贴合得严严实实）情况下，两波形的和是原波形的两倍（绿色标记的“电压”大小处9.48V的电压也印证了这一点），并且相位不变；相位相差180度的两个波形相抵消了（无论是绿色的波形还是“电压”的显示都毫无波澜）。

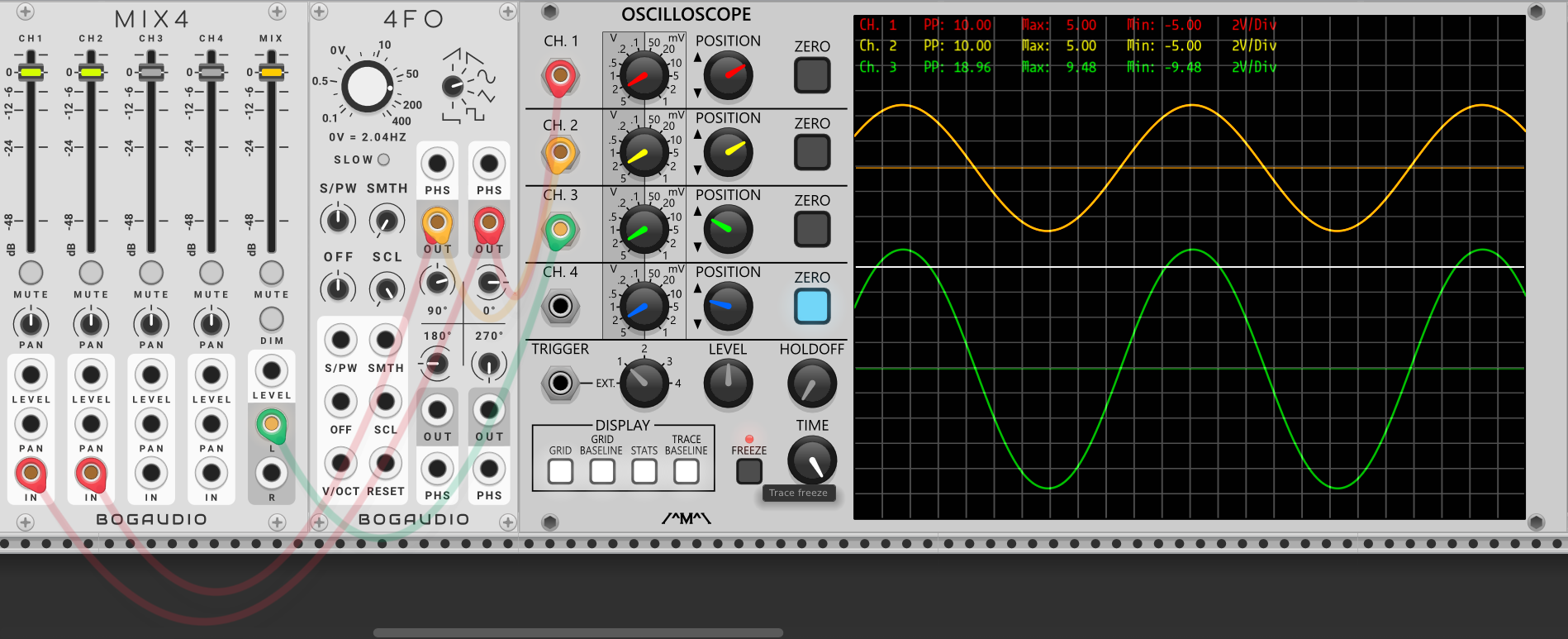
两个同相位、振幅的波形相叠加

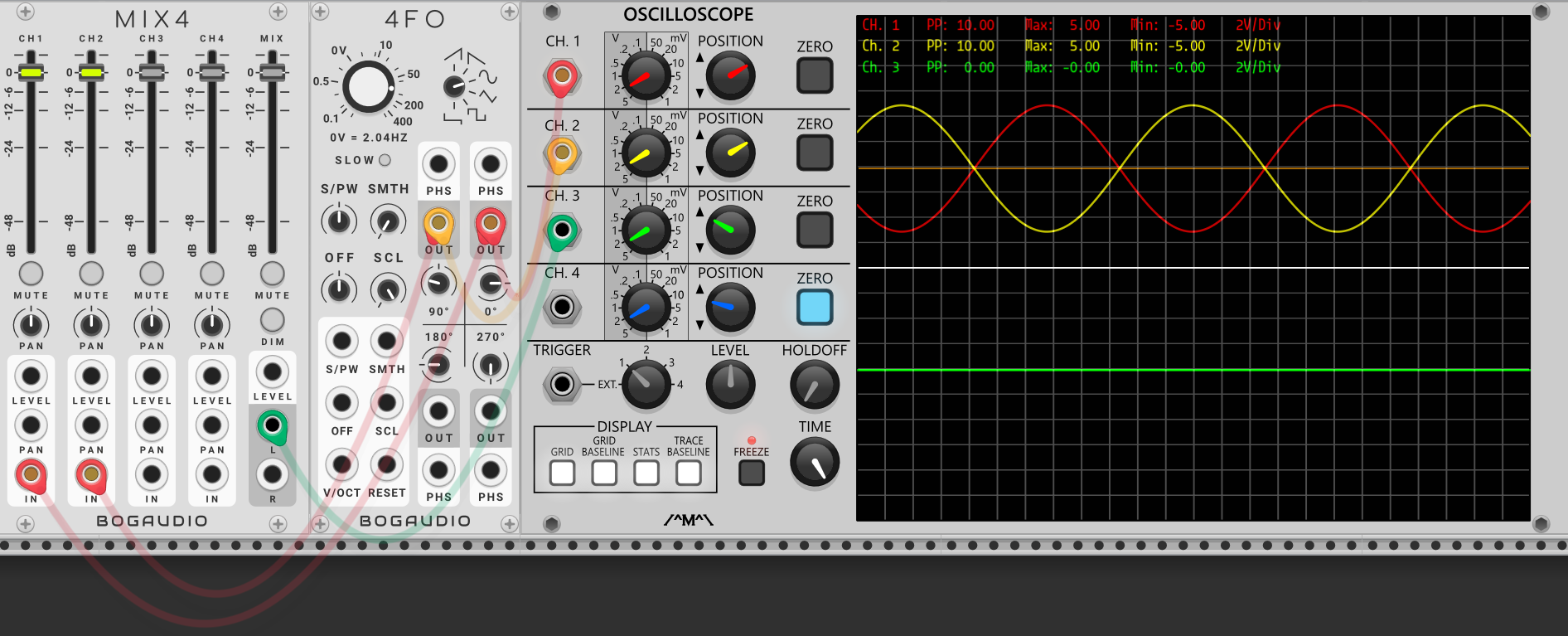
两个相位相差180度的波形相叠加

这下子我们就可以发现，对具有一定振幅的正弦波是可以使用另一个等大振幅，但不同相位的正弦波与它相加来对它进行抵消或者增强的。只不过现实生活中的模拟电路“牵一发而动全身”，波形“你中有我我中有你”，很难产生纯净的正弦波和完完全全的相位相消。芯片则能够直接对波形进行模拟和计算，最后产生“干净”的波形。现代有些数字信号合成器或是数-模结合合成器引以为傲的功能诸如：相位调制、相位失真、相位相消、梳状滤波器……都因对相位和振幅的研究而生。

回到其他被分解出来成了振幅大小不一，相位不同的正弦波信号中，那些分解出来，频率高于原始信号频率的正弦波，我们以“谐波”这个词称呼它们。傅立叶也据那些信号分解后谐波的频率和大小及它们的相位进行研究，最后提出了数套恐怖的理论和计算法则：傅立叶变换和傅立叶分析。

只不过得益于科技的发展，我们在这里并不用继续深入这套理论并搞出数页的运算过程。记住上面傅立叶的那段话，借助VCVRack模块库里“Bogaudio”制作的模块“ANALYZER”。我们即可直观地看出一个被分解后的波形在谐波分析仪显示出各个频段上正弦波的量。将振荡器200Hz的锯齿波信号直接输入给它，仔细看看它是如何显示那些谐波们的。（要学习傅立叶那套理论，去其他UP主那里找找看吧！也许那个叫“一块电鹿板”的家伙正在找合适的内容编写胎教文案——Doge）

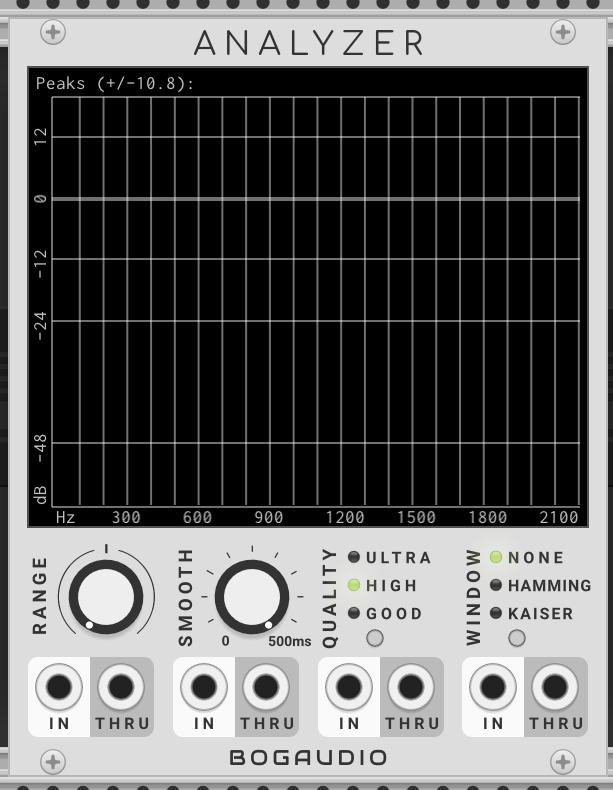
Bogaudio的分析模块ANALYZER

显而易见，不同量的谐波在分析仪上折出了不同高度的“刺”。把它们与下方的横坐标“频率”对应起来，锯齿波的谐波们原形毕露。从200Hz开始，400Hz、600Hz、800Hz……锯齿波包含的所有谐波一直延伸到了分析仪的频率极大处并渐渐消失。调整一下振荡器的频率，把它减到100Hz，分析仪上的“刺”全体向左移动，但“刺”与“刺”的间距更近了。这是因为锯齿波的谐波们遵循“锯齿波原始频率的正整数倍分布”（锯齿波谐波存在频率=锯齿波频率xA，A为正整数），频率降低后谐波的数量毫无明显的增减，而是谐波间的频率一齐降低。由于高频率的谐波于原始锯齿波的频率有较大的倍数乘积，所以降低锯齿波频率时，它们也移动得最快。锯齿波听起来“粗糙”、“丰满”、“变压器”，和它本身满满的谐波不无关系。

让我们换一个插孔，把200Hz的方波信号输入分析仪。(由于VCV Rack里自带的振荡器“VCO”基于模拟信号建模，所以它的锯齿波、方波并不是很多人想象中的那么“规整”，这也许就是模拟信号合成器的特点之一吧！)

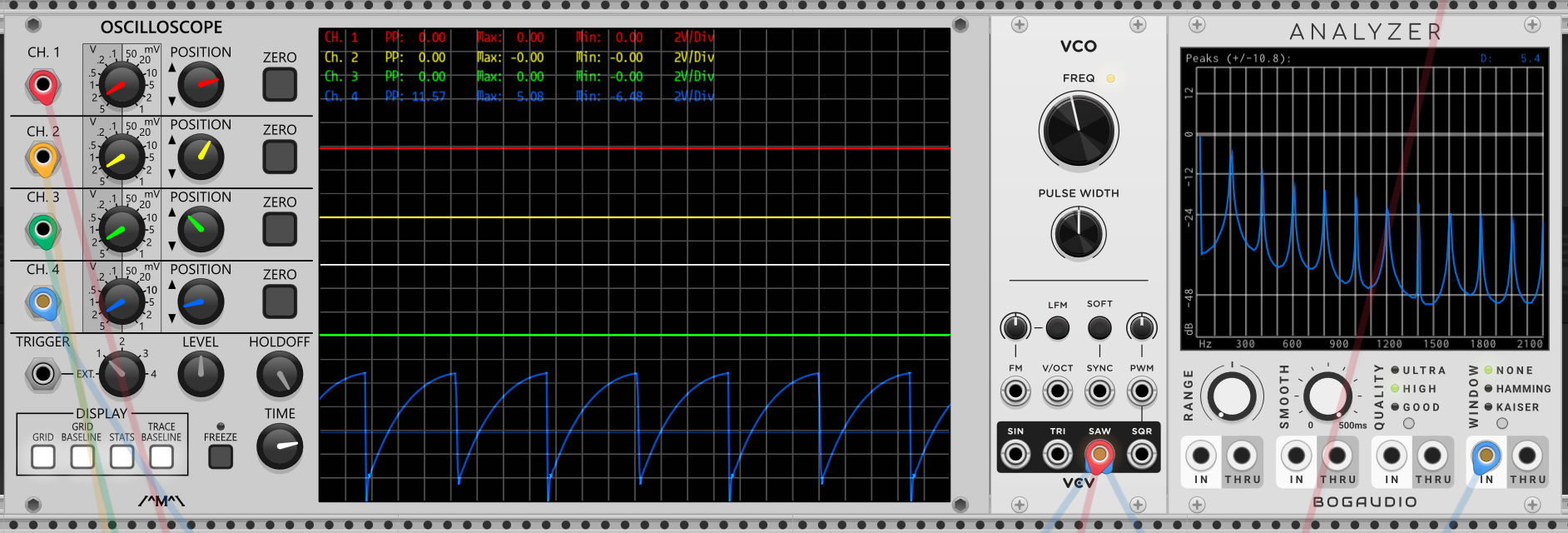
200Hz锯齿波信号分解后在分析仪上折出的“刺”

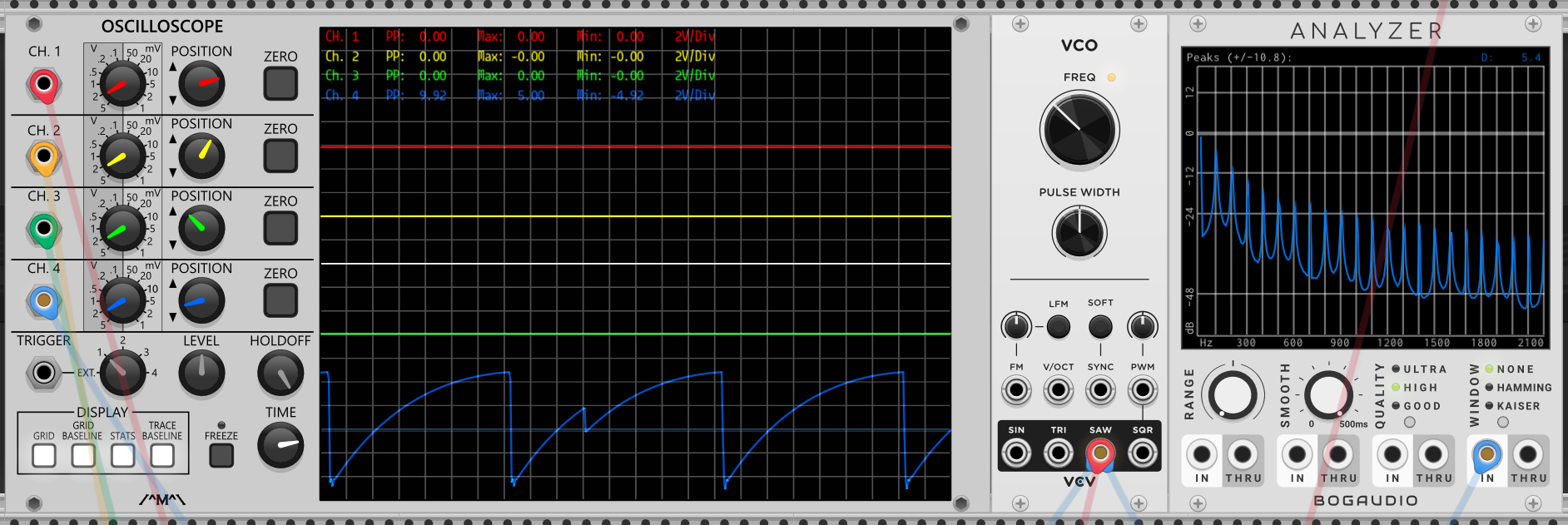
100Hz锯齿波信号分解后在分析仪上折出的“刺”

这一次，分析仪上仍然显示出了由高到低的“刺”，但是细看横坐标，“刺”生长在了200Hz、600Hz、1000Hz、1400Hz……这些坐标上唯独没有刚才400Hz、800Hz、1200Hz……等等频率的谐波。降低振荡器的频率至100Hz，分析仪上的“刺”又一次向左移动。谐波们依然只在100Hz、300Hz、500Hz、700Hz……这样有些“奇数列”的频率上存在（方波谐波存在频率=方波频率x（2A-1），A为正整数）。这下子我们就能得知，相较于锯齿波，方波原始频率偶数乘积的谐波缺乏造就了方波独特的波形和“空洞”的声音。凭借着硬件算力的提升，现在的合成器对一份复杂波形进行这样的分析、模仿，增加不同部分谐波的量，也是另一种合成声音的方法，这就近似于很久以前电子管风琴就在使用的合成思路(电子管风琴面板上那么多的推子，每推移一个，就为其振荡器输出的波形增加一个特定频率的谐波，推子移动的多少决定添加谐波的量)，这就是“加法合成”。接下来，我就选取“Bogaudio”的数个小型振荡器“Sine”来印证这个奇妙的合成思路。

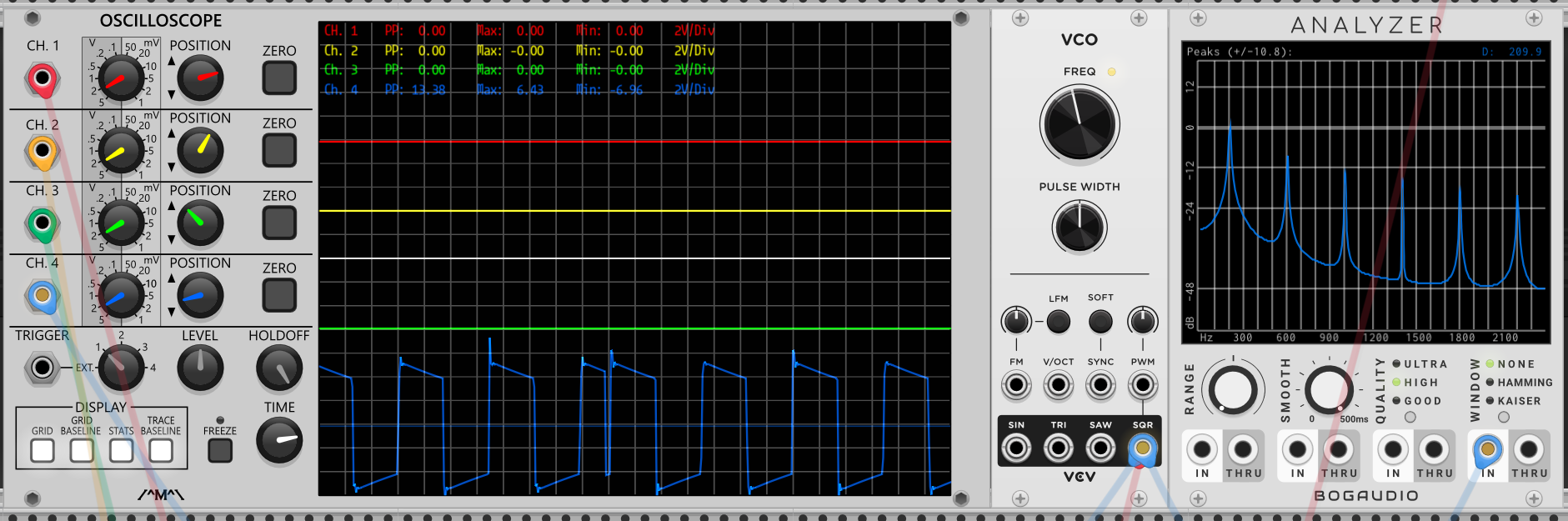
200Hz方波在分析仪上折出的“刺”

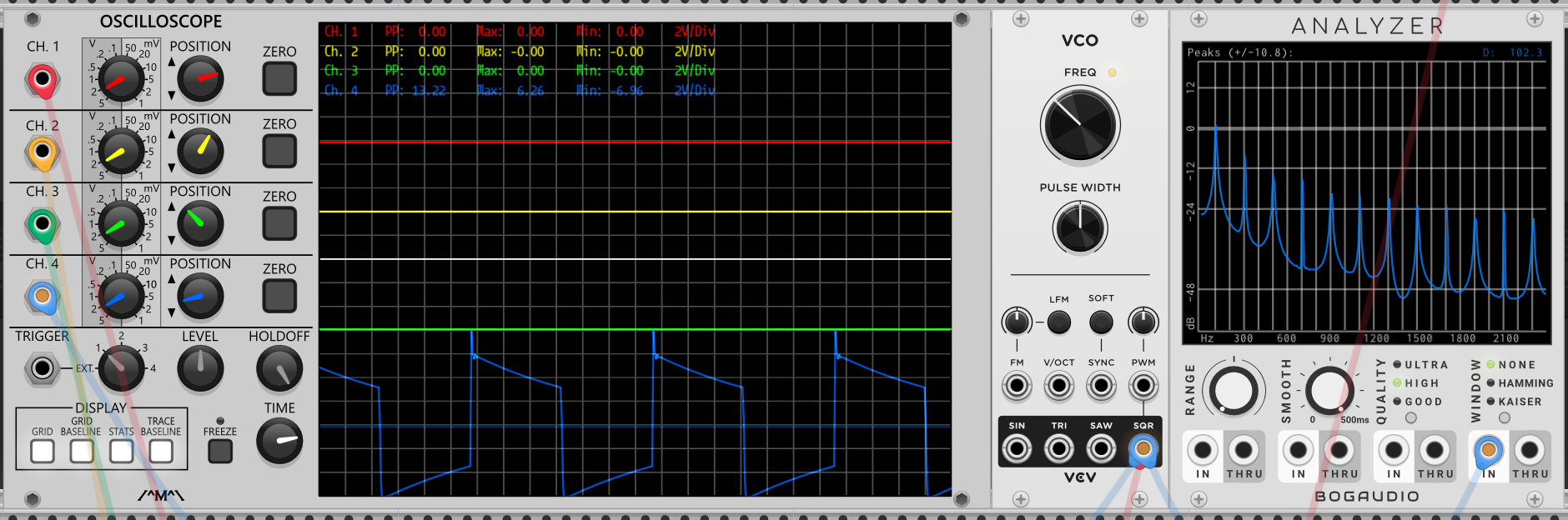
100Hz方波在分析仪上折出的“刺”

我们现在使用的“Bogaudio”振荡器“Additator”就是“加法合成”型的，右上角有旋钮“Partials”（偏音）可以调整从1到100的谐波数量。为了减少工作的难度，我们将它的谐波数量调为“8”，再使用8个产生正弦波的振荡器“Sine”和8个通道的混音器“MIX8”来一一从频率的角度，信号量的强度来模拟出这八谐波的类锯齿波，因为真正的锯齿波谐波极其丰富，在分析仪上的“刺”也消失在了无穷远处，用数十个手动调整的振荡器和混音器去模拟它，必定是一种折磨。

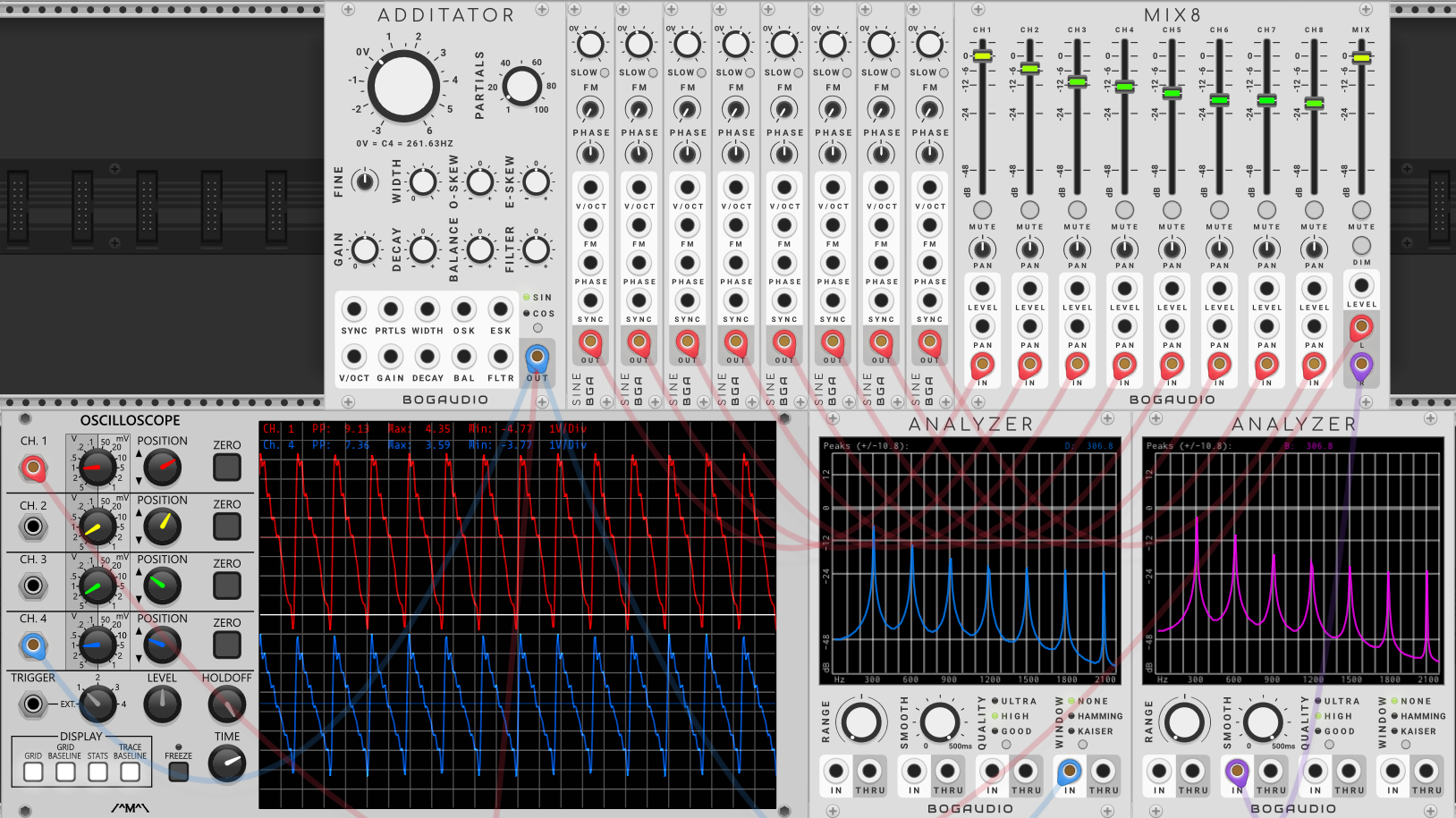
使用八个振荡器对锯齿波进行模拟

现在对比左右两个分析仪，看看示波器，听听两者的声音——几乎无法分辨！这时候，我们就学会了与传统合成器“减法合成”截然不同的合成思路“加法合成”，可喜可贺！同样得益于信号处理技术的发展，刚才拼手感的“加法合成”过程，那些黑乎乎的芯片们能以秒杀我们的处理速度和吊打眼、手的精确度叠加出谐波更多的波形，像用来演示基于谐波处理的振荡器“Additator”一样，在模块内部就把谐波处理得游刃有余，没有它“捏”不出来的波形，只有使用者没试到的谐波处理方法。

现在联结下上文讲述过的“相位”，两个相位差达180度的正弦波加在一起，两个波形相抵消了，是吧？那么放眼谐波们呢？

如果我们再编辑出另一组拟合锯齿波的振荡器，但是它们的相位与第一组一一相反，把两组振荡器产生的波形叠加在一起，结果如何？叠加后的波形在分析仪上折出的“刺”又有了什么样的变化？为了方便对比，我使用“Bogaudio”的可调相位低频振荡器“4FO”输出200Hz的锯齿波来进行测试。

是的，猜一猜也能知道，第一组振荡器的信号被第二组振荡器产生的信号削弱了不少，信号在示波器上的波形也降低了不少高度，但仍未能将谐波丰富的锯齿波完全抵消。甚至600Hz、1200Hz、1800Hz……的谐波还得到了增强——也就是说，叠加后的新波形成了频率为600Hz的锯齿波！正是因为两个锯齿波丰富的谐波在相位改变时互相产生了抵消、叠和等一系列复杂的过程，因此新的波形将面临着波形和频率的改变，特别是拥有多个谐波的复杂波形。

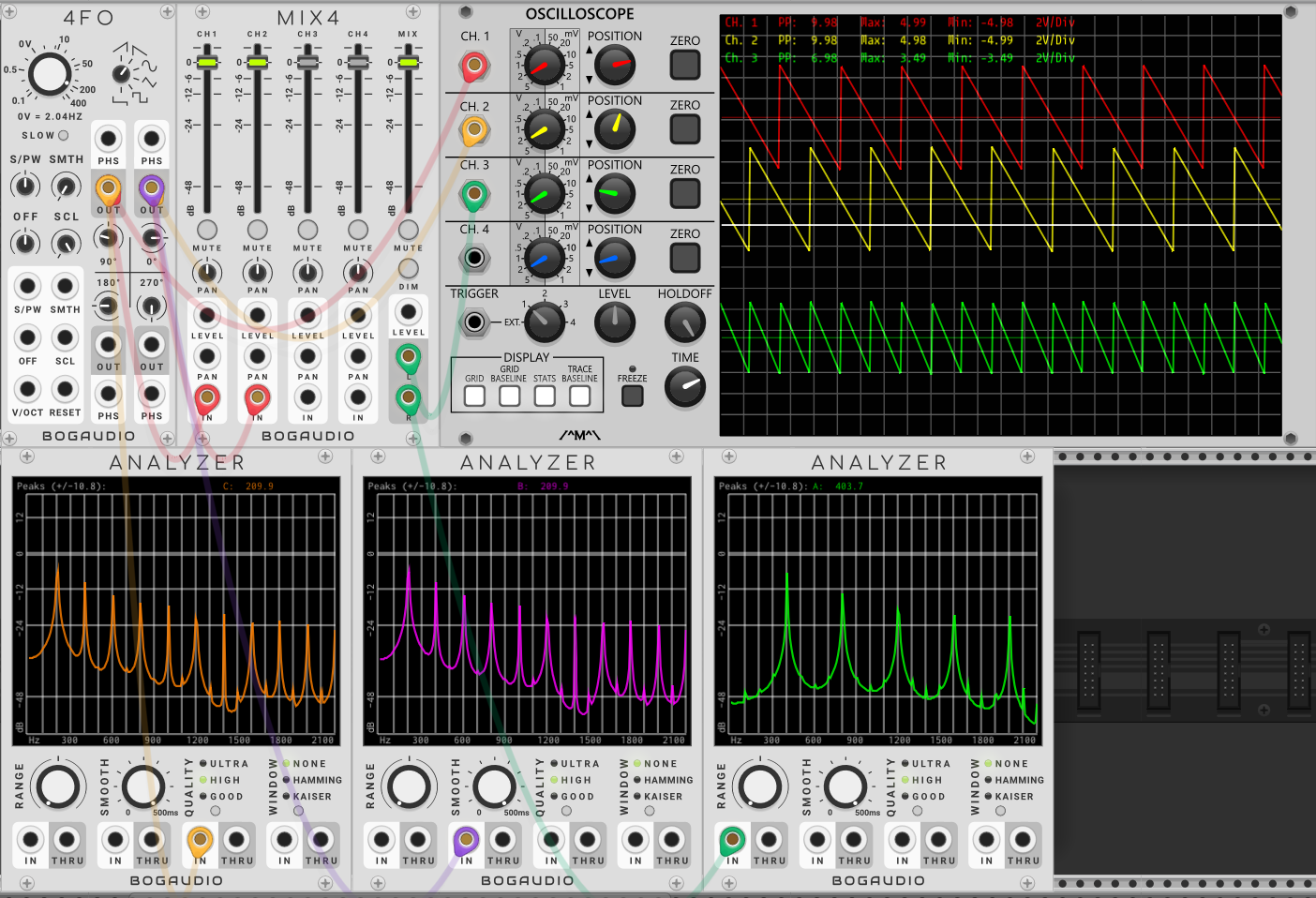
相位差达180度，同频率的两个锯齿波叠加

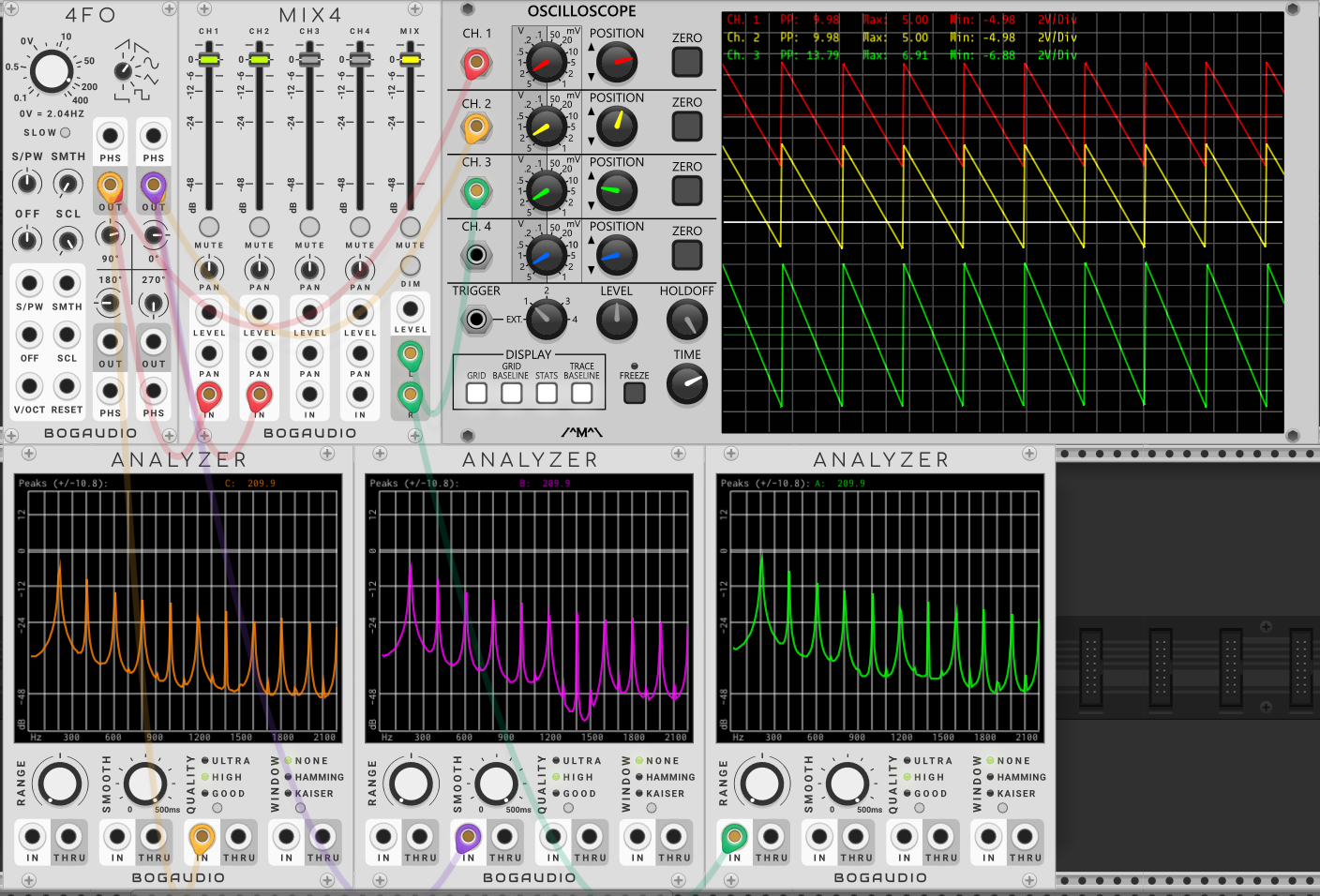
同相位、频率的两个锯齿波叠加

换句话说，当除了相位偏移之外其他方面完全相同的两个波形叠加在一起时，两个波形的谐波相位差导致了滤波。回想起分析仪上连续的“刺”，它们的形状与梳子十分形似。使用谐波相消的滤波时，这在分析仪上像极了断了数根梳齿的梳子，所以使用这一技术的滤波器被称为“梳状滤波器”（Comb Filter）。梳状滤波器在合成器中被广泛运用，从经典的模拟信号合成器到基于数字信号的合成器上都可以找得到到梳状合成器的身影。只不过有些时候，因为它处理后的声音可以混乱而疯狂，它也用作效果器。

了解了关于相位的的知识之后，不难看出相位与滤波之间关系密切。但再仔细思考一下，相位变化可以导致滤波，那么滤波能否导致相位变化呢？答案是：当然可以！

谐波的聚合造就了锯齿波、方波这样各具特色的波形，这其中也包含着谐波相位的叠加。滤波器对于谐波的削减也是对相位的削减，结果在最终生成的波形上往往会起到“一着不慎，满盘皆输”的影响。

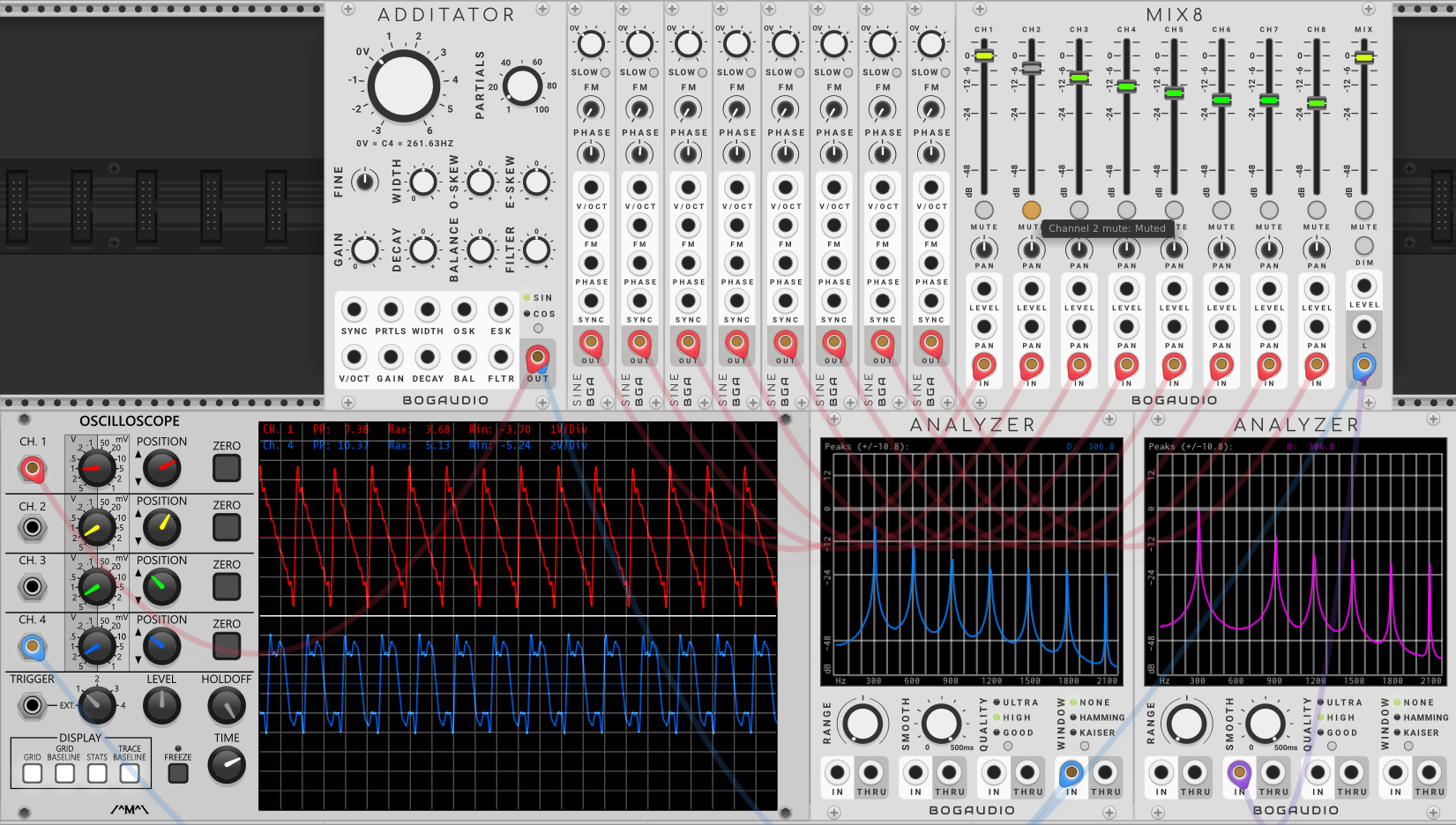
失去了600Hz谐波的基频为300Hz的拟锯齿波波形和300Hz八谐波的拟锯齿波波形

虽说了解一个波形的本质并不在介绍VCVRack基础模块的范畴里，但那些模块们对波形施展的奇妙“魔术”，究其原因就是对谐波的处理。从经典的“减法合成器”开始，滤波器的使用就开启了对波形谐波的探索，并以此衍生了数种处理谐波的方式：从高频到低频削减谐波——低通滤波；从低频到高频削减谐波——高通滤波；从高低频之间的中频削减谐波——带阻滤波（陷波滤波）；同时从高低频削减谐波——带通滤波……这与下一篇介绍滤波器的种种不无关系，也会为后续理解一些塑形器、效果器的工作原理给予不小的帮助。至于分析滤波器的工作情况，和它们为什么有的以“24db/oct”分类，或是以“4-Pole”分类，就留到下一章再去深入吧！最后，我希望和我同样喜爱合成器的读者们能够在波的海洋里积极地“畅游”。