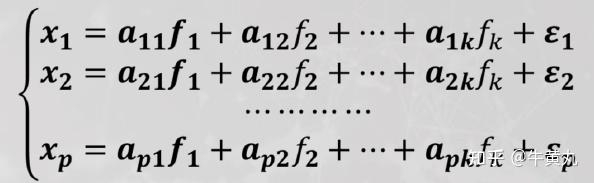
因子分析的模型

1、设原始变量为x1,x2…xp

2、因子为f1，f2，…fk

3、原始的p个变量可以表达为k个因子的线性组合变量。

因子分析的数学模型基本的概念

1. 公因子： 因子 1, 2 ⋯ 由于出现在每个原始变量与因子的线性组合中，因此也称为公因子。

2. 因子载荷：系数 如 11、 12等就是因子载荷。反映了变量与因子之间的相关程度，相当于回归系数。绝对值越大，该因子与变量的关系越强。

3. 变量共同度：所有公因子对该变量信息的解释程度。/> \sum_{j=1}^{k}{a_{ij}^{2}} = ( = 1， 2 ， ⋯ ， )如果大部分变量的共同度都高于0.8，则表示提取出的公因子可以反映原始变量80%以上的信息。

3. 方差贡献：因子 对于所有原始变量总方差的解释能力。反映第j个公因子的相对重要程度,其值越高，说明该因子的重要程度越大。r/>

因子分析的步骤

1. 检验数据是否适合做因子分析： 相关系数矩阵、巴特利特球度检验、KMO检验。Bartlett球度检验

以变量的相关系数矩阵为基础，假设相关系数矩阵是单位阵(对角线元素不为0，非对角线元素均为0)。如果相关矩阵是单位阵，则各变量是独立的，无法进行因子分析KMO检验

用于检验变量间的偏相关性，KMO统计量的取值在0～1之间；

如果统计量取值越接近1，变量间的偏相关性越强，因子分析的效果就越好；

KMO统计量在0.7以上时，因子分析效果较好；KMO统计量在0.5以下时，因子分析效果很差。