01引言

在圆锥曲线题目中，我们有时会遇到一类需要求出焦半径的值或表达式的题目。解决这类题目，我们最常用的是用半长轴、离心率和横坐标（以焦点在x轴上为例）来表出焦半径的“±a±ex”。例如，在图1（见02部分）中，F为左焦点，A为椭圆上横坐标为x的一点，我们即可确定AF=a+ex。这个公式是熟知的，其证明也不依赖圆锥曲线第二定义，甚至对人教版教材上圆锥曲线方程的推导过程中挑选其中一步加以整理就能得到，因此这里略去，读者朋友可以自行完成。

然而，点的坐标并不总是非常好求。当题给条件是焦点弦的方程时，如果我们试图硬解其与圆锥曲线的交点，运算量是相对可观的。如果里面还带有参数，最终即便运算完全正确，表达式同样也是很大概率“不堪入目”的。这时，我们想问这样一个问题：是否存在一种不需要求交点坐标，只根据焦点弦方程和圆锥曲线方程就可以给出焦半径的方法呢？答案是肯定的。

02公式的推导

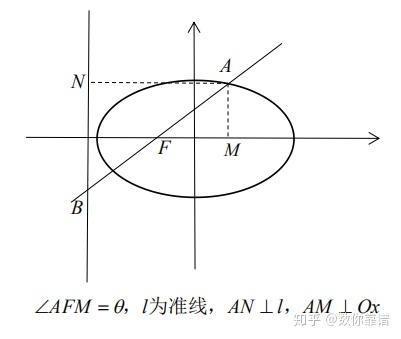
建构起这样一个可以应用第二定义的体系后，我们来推导焦半径公式。

这样，我们就得到了想要的焦半径公式，下面我们利用这个公式给出几个直接推论。

03直接推论

推论1：另一侧焦半径，通过类似方法我们可以得到

推论2：焦点弦长为两半径之和

推论3：两焦半径之比

推论4：当焦点弦过右焦点时，类似方法可知我们只需要将焦半径公式分母中的“c·cosθ”项前的正负号改变即可，读者自证不难。

04简单应用

对于文中推出的公式，我们举出两个例子展示其应用。

例1：已知焦点弦的比例关系求离心率

由推论3可以立即得到，因此证明从略

例2：焦点弦的中垂线

04下期预告

在这期推送中，我们初步探究了焦半径的表达、推论与两个简单的应用。但是，这还不足以充分地展示出这种焦半径公式的魅力。在后面的推送中，我们还将再回到这个主题，利用本文给出的焦半径公式，处理一些更复杂的问题，也尝试探索一下这一公式的本原形式，敬请读者朋友们期待。

最后感谢大家的阅读，我们是“数你靠谱”公众号，欢迎各位批评指正，我们期待您的关注和支持！