二、验证性因子分析（Confirmatory Factor Analysis, CFA）

前面我们也分析过EFA和CFA的区别，我再重新总结一下（找到一个简洁的）：

CFA的进行必须有特定的理论观点或概念架构作为基础，然后借由数学程序来确定评估该理论观点你所导出的计量模型是否适当、合理，因此理论架构对CFA的影响是在分析之前，其计量模型具有先验性，理论是一种事前的概念。（邱皓政，2005）

简单来说（说人话）：如果你的模型是别人的已经研究过的模型，同时，你的各变量的题项是确定的（参考别人的），各变量的维度也是被验证过的，同时各维度的题项也是已知的，通过检验的（有人用过的），那就要用CFA

关于CFA我们采用的工具是AMOS或者是Mplus，我们主要讲AMOS，因为比较简单基础，如果有时间，后续会更新Mplus的操作过程和结果解读。

AMOS具体操作过程：

打开AMOS软件，我们会有这样的画面：

刚使用的朋友可能没有感觉，但是使用过的朋友，特别是我这类的美术功底不怎么样，又没有耐心的朋友，一般都会有这样的烦恼：这操作界面（纸）太小了，不够画。。。盖亚。。。所以在操作之前，我建议大家把纸张调大一点，这样既美观，也方便最后的复制。具体操作如下：

View→ Interface Properties

然后根据需要调节就行了，我一般选择A4。。作为灵魂画师的我感觉够画了。。

主要讲解一个核心内容：

方框和圈圈的区别：方框代表观测变量，椭圆代表潜变量，小圆圈代表误差。

在行为科学领域，有许多假设构念是无法直接被测量或观察到的。如焦虑、态度、动机、压力、满意度等等。这种假设构念知识一种特质或抽象的概念，无法直接得知，要得知人们在这些构念上的实际情况，只能间接以量表或者观察到的实际指标数来反应该构念的特质。举个栗子：“工作满意度”是一个构念，也就是潜变量，他对工作是否满意取决于很多方面，比如“对工作环境是否满意”“对薪酬是否满意”“对工作中的人际交往是否满意”等等。上述具体的满意指标就是工作满意度的指标变量，或者成为显著变量、观测变量。如果具体的满意指标越多，那么对一个人的工作满意度判断的正确性会越高，可信度也越好。

观察变量与潜变量的关系如下：

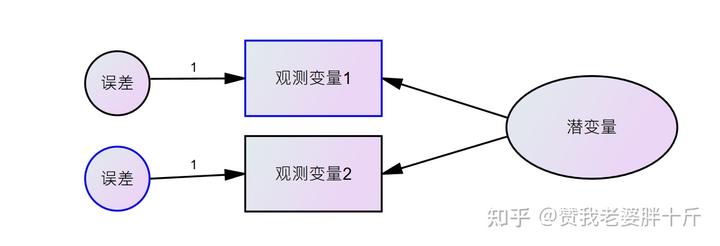
注意：一个潜在变量必须以两个及以上的观测变量来估计，成为多元指标原则。在SEM分析中，观察变量一定存在，但潜变量不可能单独存在

例子：

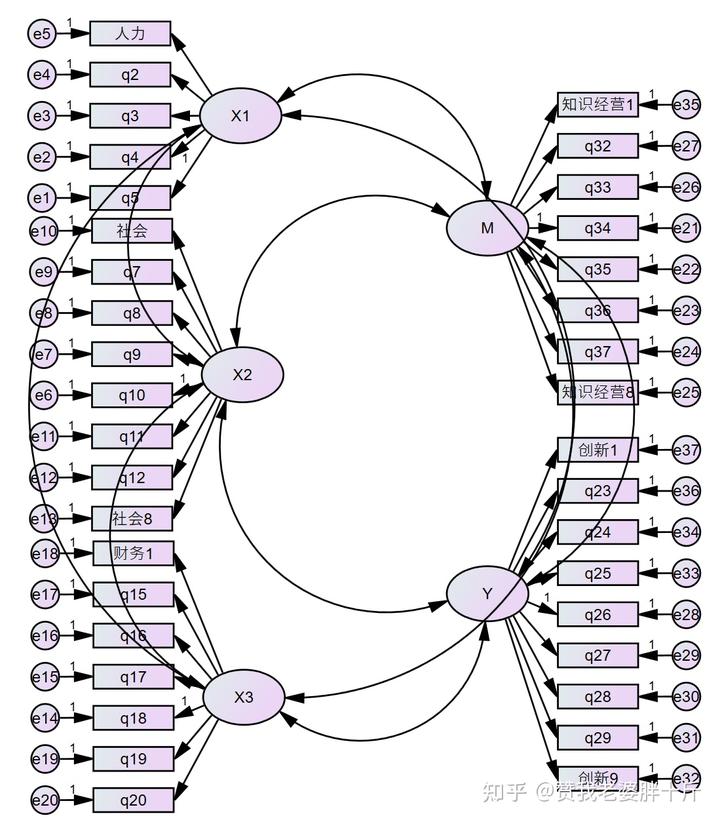
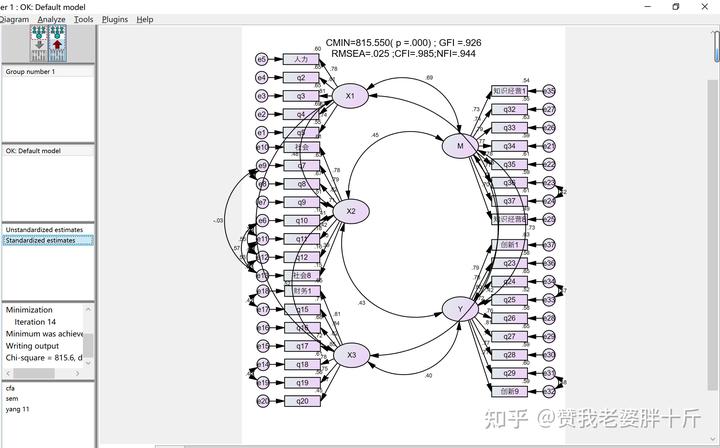
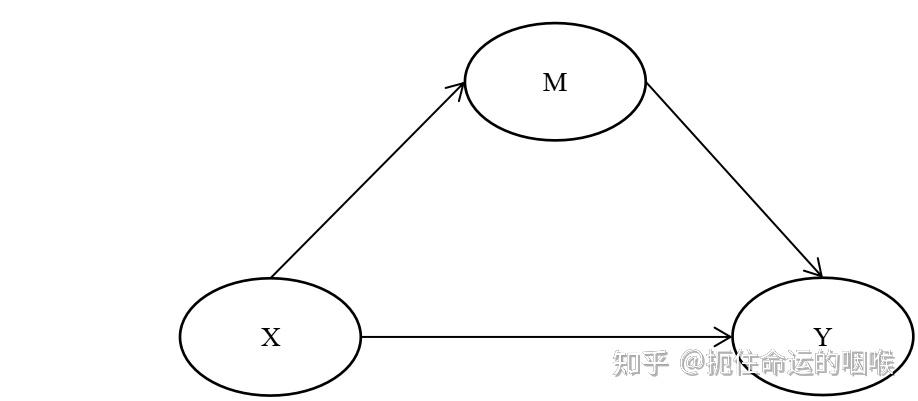
已知，X1,X2,X3是三个不同的自变量，M为中介变量，Y为因变量，他们的假设模型如图所示。

X1的测量题项：x1.1—x1.5

X2的测量题项：x2.1—x2.8

X3的测量题项：x3.1—x3.7

M的测量题项：m1—m8

Y的测量题项：y1—y9

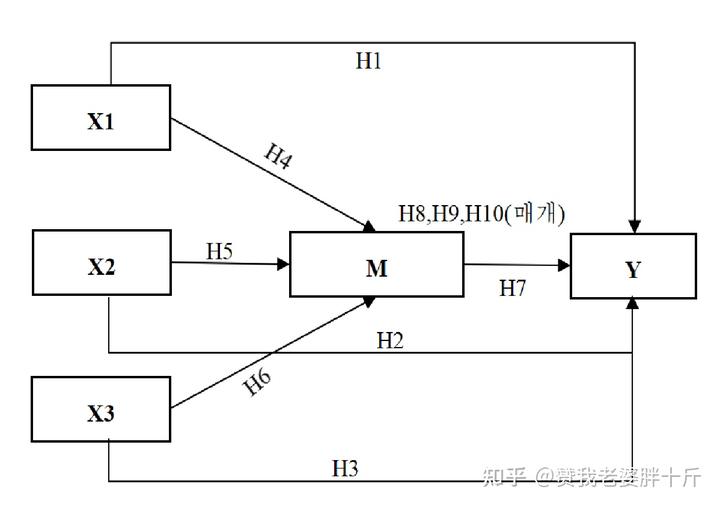
理论模型图运用AMOS进行模型绘制

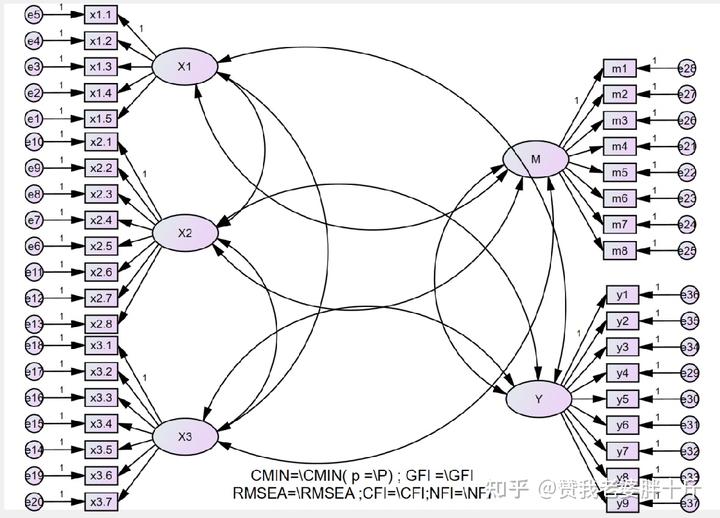
验证性因子分析拟合模型图 我们如何制作这种图？（建议具体操作看视频）

（1）在空白处画一个椭圆，然后选取第一行第三列图标，在椭圆形上连续点击若干下，点击一次会在椭圆形上方出现一组测量指标与误差项，点几下取决于你的潜变量中，有多少个观测变量，有几个观测变量（测量题项）我们就点几下。

（2）点击（选中）第三列第十行的按钮，然后点击复制按钮，向旁边移动，就可以整个复制潜变量和观测变量的 部分。用相同的办法将自变量、中介变量和因变量画出来。

第三列第十行的Preser ve symmetries按钮

（4）导入数据。点击第八行第一列的图标如图所示。然后点File Name选择SPSS格式（.sav）保存的文件，点击OK。

（5）填充观测变量。点击第三行，第三列的按钮。如图所示：

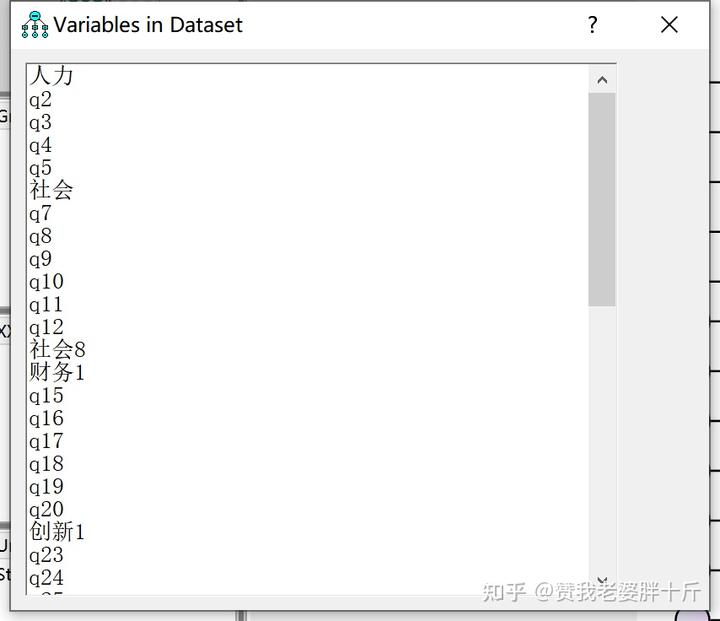
然后我们根据我们的理论模型，将观测变量（测量题项）填入方框中。

然后对潜变量命名，这里面有一个细节需要注意，潜变量的名称不能和.sav文件中的变量名称一样或有重复的。要不然计算不出结果！，因此我们选择系统自动命名。

Plugins→ Name Unobserved Variables

然后我们对潜变量的标签进行命名。（标签和名称不同，标签和SPSS文件名称相同没有影响）

（6）建立相关关系。

方法1：连接相关关系的线。第二行第二例的图标，对潜变量间两两互相建立相关关系；

方法2：系统自动连接。首先用单手指选中潜变量，然后点击Plugins → Draw Covariances

绘制完成后如下图所示：

（7）然后输入TITLE。点击第三行第一列Title图标。在画布中点击空白处，如图所示：

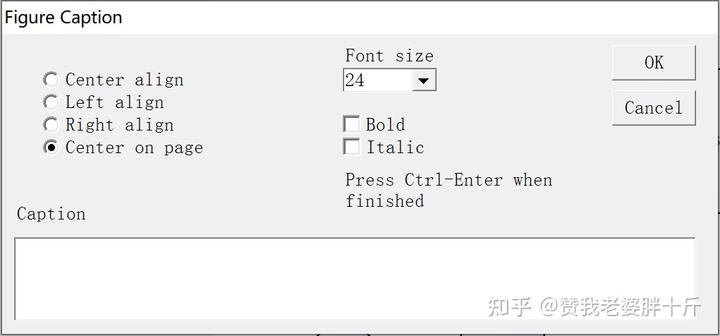
然后在方框内输入：

CMIN=\CMIN( p =\P) ; GFI =\GFI
RMSEA=\RMSEA ;CFI=\CFI;NFI=\NFI

输入的内容意义我会在结果解读中详细说明

（8）输出结果选择。点击第八行第二列图标，然后点击output，如图所示：

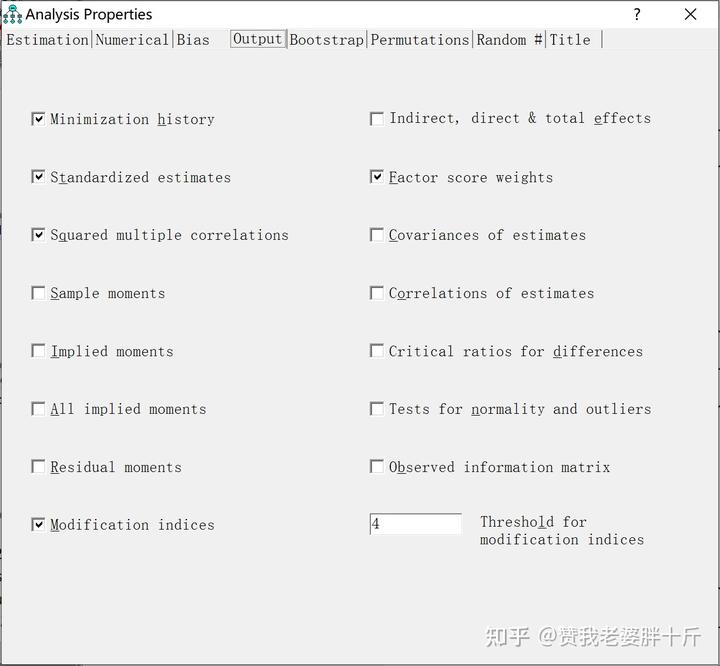
如果仅仅知识用AMOS做验证性因子分析，只需要勾选“修正指标”（Modification indices）即可。

（9）然后点击计算（第八行第三列的图标）。

到这里为止，具体操作步骤就讲解完成，我补充一点无法跑出结果的原因，同学们要注意自查和避免：

1.潜变量间没有画相关关系的线。

2.潜变量名称与.sav格式文件中的变量名称冲突或

3.潜变量误差项没有命名。

4.没有标选误差项

那么结果我们该如何看，模型拟合的判别标准又是什么？

点击计算以后，可能会出现没有弹出结果表页面的情况，这时候，不要慌，点击第九行第二列的图标即可。

输出结果如图所示：

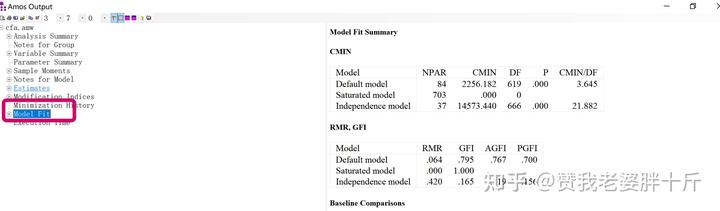
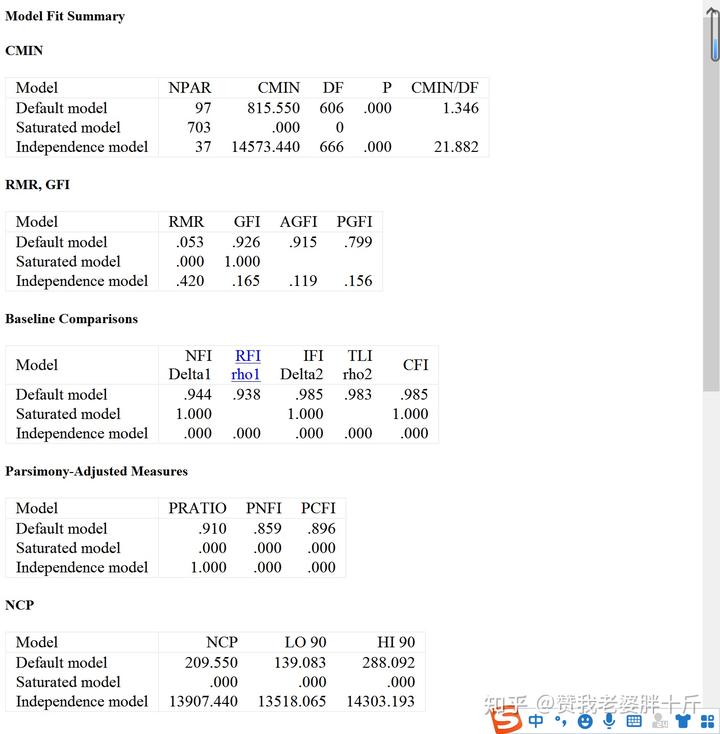
点击左边菜单栏的Model Fit，我们主要的模型摘要分析都在这些表里面。如图所示：

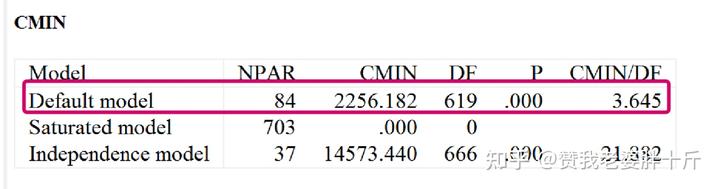
模型适配参数会提供预设模型（Default model)

饱和模型（Saturated model)

独立模型（Independence model)

判别指标： CMIN/DF＜2（＜3）P＞0.05

由于卡方值容易受到样本量的影响，当样本量较大时，卡方值相对地也会变大，显著性概率P值会变小，容易出现假设检验被拒绝的情形，必须进行模型修正才能有效适配样本数据。因而，如果在大样本（n>200)的情况下，判断模型假设与样本是否适配，除了参考CMIN外，也必须考虑其他适配度统计量。（P小于0.05也不需要在意）

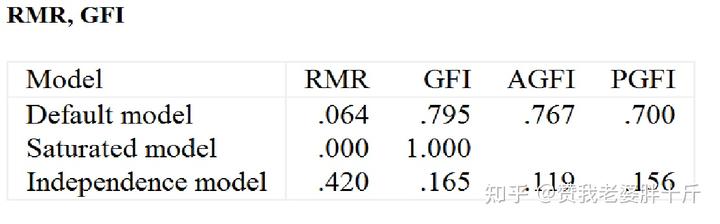
判别指标：RMR＜0.05 SRMR＜0.05 GFI＞0.95（＞0.9） AGFI＞0.9

SRMR 计算方法：

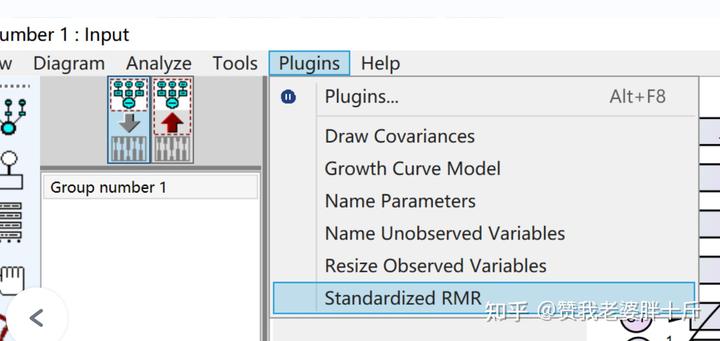
Plugins → Standardized RMR，然后弹出如下图所示的对话框：

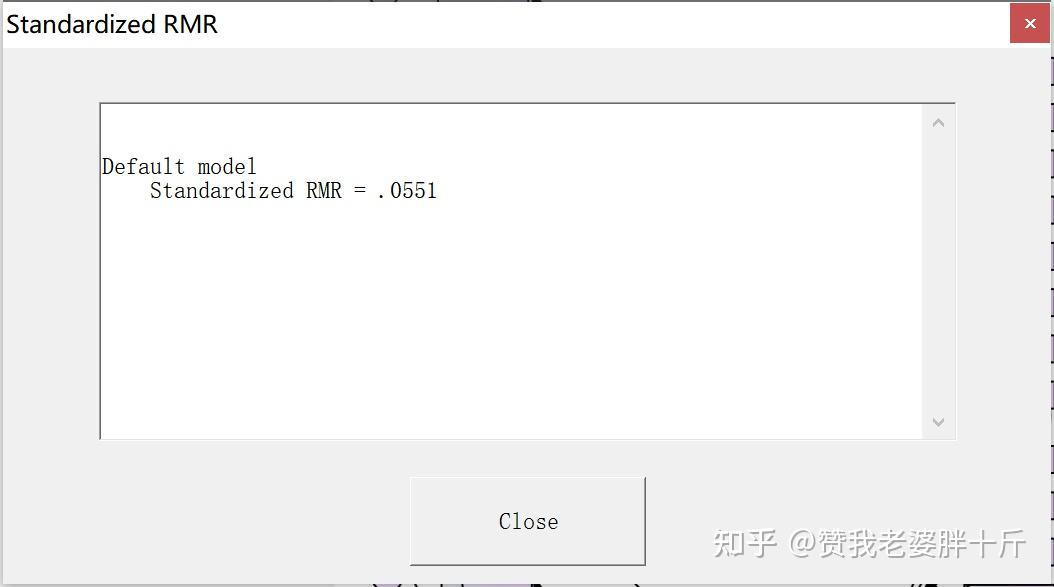
然后保持对话框存在的状态，再次点击计算即可得出结果。

判别指标：CFI＞0.95（＞0.9）TLI＞0.95（＞0.9）IFI＞0.95（＞0.9）

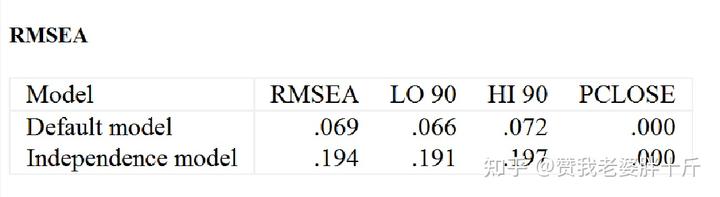
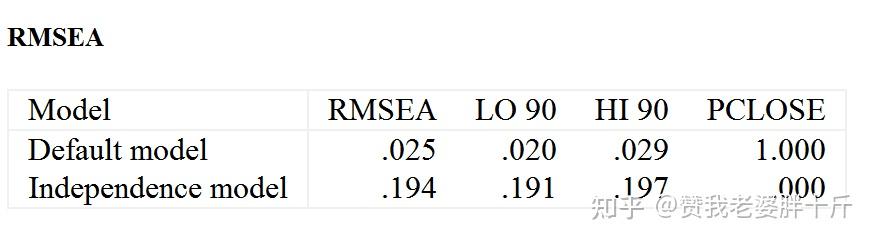
判别指标：RMSEA＞0.1 模型适配欠佳；0.08＜RMSEA＜0.1模型尚可；0.05＜RMSEA＜0.08模型良好；RMSEA＜0.05 模型适配度非常好判别标准如下：

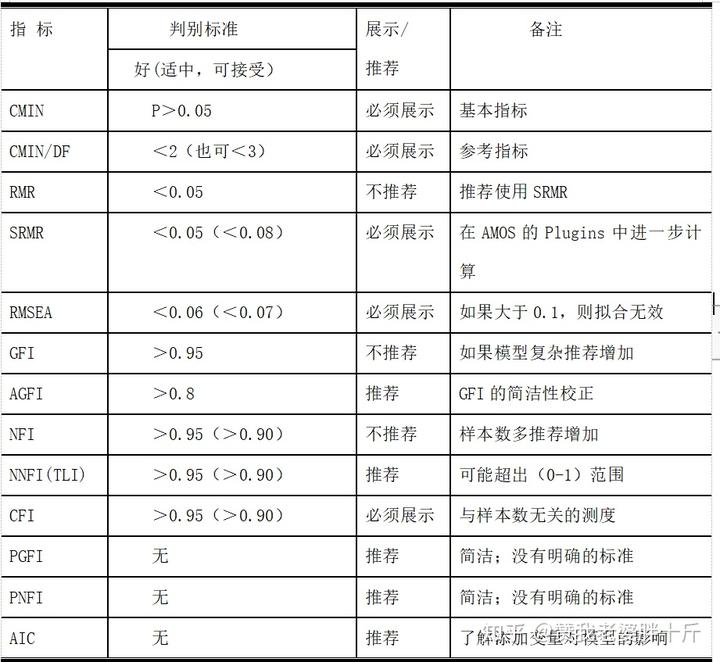
所以，综上所述，我们需要在结果输出表中展示的指标有：CMIN、CMIN/DF、SRMR、RMSEA、CFI。（和Title中输出的内容是一致的）

我们发现结果指标大多不符合判别标准，需要进行修正。

多数情况下，执行结构方程建模并不能一次就得到理想的模型。如果模型拟合数据不理想，可能是数据的问题，也可能是模型的问题或理论本身的不足。因此处理模型拟合不理想的方法有：

1、对原模型重新定义形成新的模型；

2、收集新样本在对原模型进行验证；

3、根据修正指数（Modification Indices)修正模型；

相比而言，前两种方法更严谨，但在实际研究中，研究者往往会根据修正指数的提示对模型进行修正。修正指数是基于残差分析的统计指标，完全由数据驱动，如果全部接受MI的提示，最后得到的是饱和模型，此时数据和模型是趋于完美的，所以在根据MI进行修改时一定要有理论依据或在逻辑上说得通。

（1）首先，在结果输出表中，找到 Modification Indices

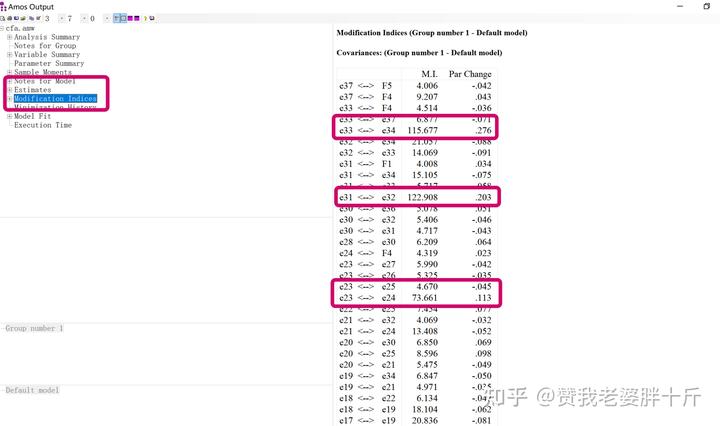
（2）如图所示，我们可以看到M.I值，我们根据这个值来进行修正。找到M.I值最大的那一对，在他们之间建立双向的相关关系。

建议：从M.I.值最大的那一对开始，把M.I.＞50的全部添加，一般来说，结果就会达标。

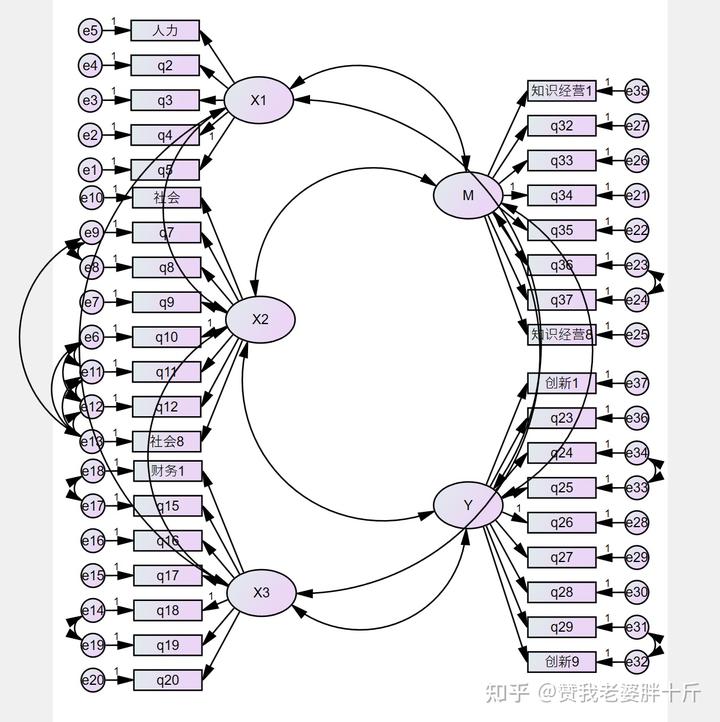
*需要注意的一点是潜在变量（共同因素）与测量误差间不能有共变关系或因果关系路径存在。

最后，点击图标（红色箭头那个）即可查看各变量间的未标准化系数和Title的输出结果了。

补充说明：首先，我们设 X 为自变量， M 为中介变量， Y 为因变量。模型假设如下：

测量自变量 X 的题项为 X_{1},X_{2},……X_{10} 测量中介变量 M 的题项为 M_{1}，M_{2}……M_{10} 测量因变量 Y 的题项为题项为 Y_{1}，Y_{2}……Y_{10}

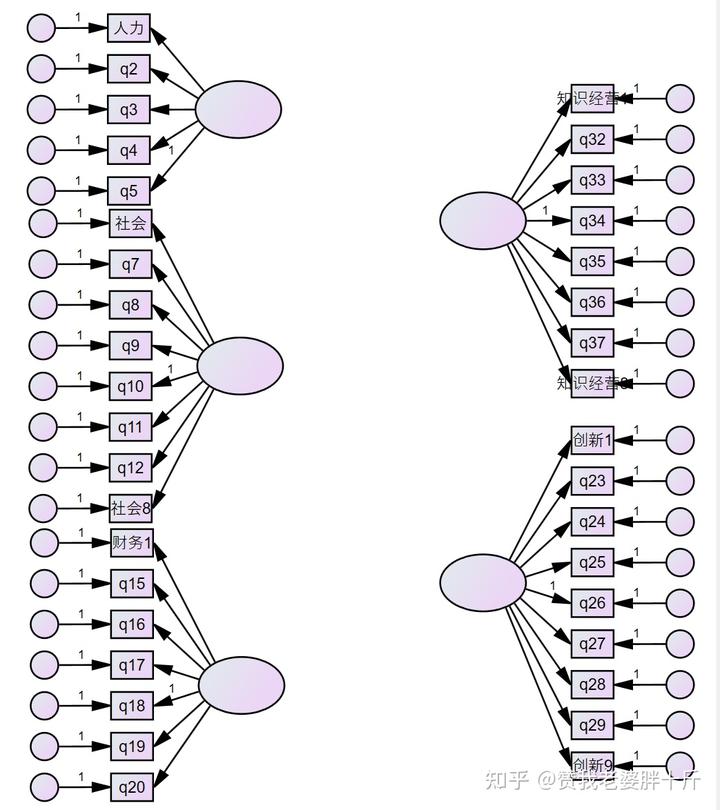
情形1：X,M,Y 均只有一个维度，即均为单维度变量。此时验证性因子分析的结构图比较简单，这也是各位朋友比较熟悉的做法，我们将 X,M,Y 作为潜变量，各题项作为观测变量进行模型构建，测量模型如图所示：

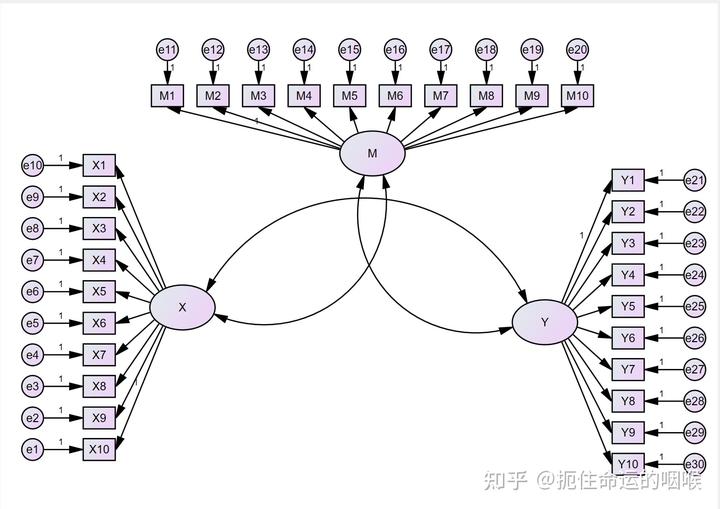
情形2：自变量 X 有两个维度，分别为 X_{a}和X_{b} ,中介变量 M 有两个维度 M_{a}和M_{b} ,因变量 Y 有两个维度 Y_{a}和Y_{b} ，研究模型假设如下：

测量自变量 X_{a} 的题项为 X_{1},X_{2},……X_{5}

测量自变量 X_{b} 的题项为 X_{6},X_{7},……X_{10}

测量中介变量 M_{a} 的题项为 M_{1}，M_{2}……M_{5}

测量中介变量 M_{b} 的题项为 M_{6}，M_{7}……M_{10}

测量因变量 Y_{a} 的题项为题项为 Y_{1}，Y_{2}……Y_{5}

测量因变量 Y_{b} 的题项为题项为 Y_{6}，Y_{7}……Y_{10}

这个时候如果我们用上面的做法，那么测量模型如下：

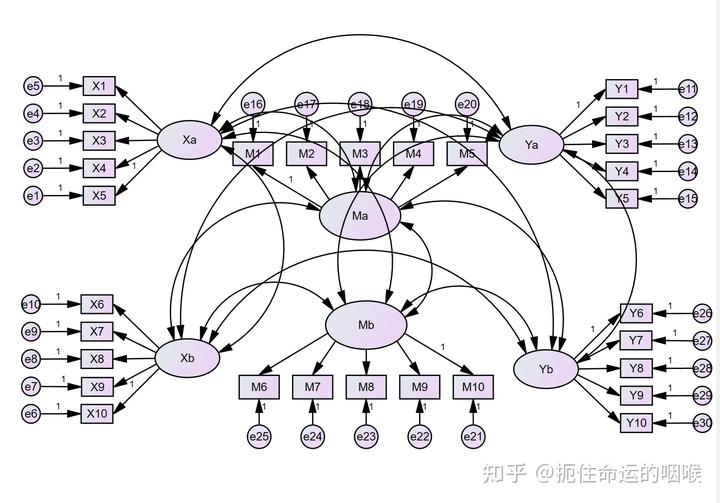
以下内容是个人理解，并未得到广泛承认。这个测量模型有一定的局限性：

1、当变量维度较多、测量题项较多时，测量模型很难画，共变关系太多图形很复杂。

2、这个测量模型图并不能展现X，M，Y三个变量之间的关系，都是维度间的关系。

因此我们可以以下两个方法来进行测量方法一：用维度均值代替各变量的题项。

方法2：用二阶验证性因素分析

用这两种方法画的测量模型图就能表现出X,M,Y三者之间的关系。所以，各位可以根据自己的需要，画自己的测量模型图。

调节变量也需要画入模型图中。验证性因子分析，只是分析变量间的协方差，因此不需要考虑变量间的具体因果关系。所以，验证性因子分析，无论你有几个变量，全部都要画出来，用双箭头建立相关。