向量部分的题目也比较容易，我们在这里重新理解一遍这部分基础概念间的逻辑关系，以便大家能够更好的建立知识体系，能够站在更高处看清问题。

我们首先思考几个问题来引入话题。

1.为什么要有向量这么一个东西呢？

2.高中物理课程中，一开始就提出了向量的概念，用来表示力、位移、加速度等物理量。那么问题来了：向量是首先从物理学发展出来的呢，还是首先由数学家提出来的？

（有人跟我说，物理里的是矢量，数学里的是向量，那我只能说其实它们的英文名字叫vector）

3.上面这个问题，看起来没有什么意义。那么我们接着问：向量加法满足平行四边形定则，力的分解也满足平行四边形定则，这两者之间是什么关系呢？

4.我们定义了向量的点乘运算： a∙b=|a||b| cosθ ，然后可以用来证明很多几何问题，比如证明平面几何的余弦定理：

从而，根据点乘的定义有， a^2=b^2+c^2-2accosθ

但是，如果我们定义向量的点乘为a∙b=|a||b| sinθ，余弦定理就没法用向量方法证明了。但可不可以这么定义呢？

5.坐标表示是解决向量问题的有力武器，那么历史上是现有了向量理论，然后根据需要产生了向量的坐标方法吗？

在回答上面几个问题之前，我们先重复一个信念：世界是美的，数学也是美的。

不论是从结绳计数抽象出1+1=2，还是从“两点之间线段最短”抽象出欧式几何，数学以其简洁严谨的形式完美的描述着这个世界的万事万物。

实在有点美，忍不住盗图，侵删

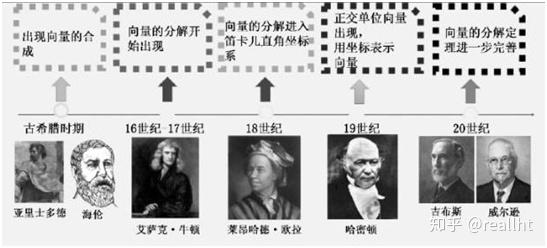
向量分析理论的形成和发展经历了近千年的时间，凝聚了一代代数学物理学家们的心血和智慧，国内外也有很多专门研究向量发展历史的著作，但都比较深入复杂，不好理解。下面的概括可能有失偏颇，但应该比较好理解：

首先，古希腊亚里士多德在研究速度问题时，发现他们遵守平行四边形法则，后来斯蒂文、牛顿等学者在研究力的分解合成时也发现了这个规律。所以，平行四边形法则不是人为定义的，它是经过大量试验和观察总结出来的公理。

但是，明确的向量定义是数学家们提出的。而且他们提出向量也不是因为对物理学的研究，而是在研究复数在坐标系里的几何表示时定义了向量及向量的坐标方法。

向量作为工具研究几何、物理问题，开创了研究几何、物理问题的新方法。比如，欧氏几何只依据基本的逻辑关系，从公理出发，通过演绎推理来证明问题，过程严谨优美，但没有一般的规律可循，存在较大的思考难度。引入向量和向量的运算的意义是为几何和物理研究提供强大、有力的工具；引入向量的坐标表示的意义是为了提供更简洁的工具。

至于为什么定义向量的点乘为： a∙b=|a||b| cosθ，而不是： a∙b=|a||b| sinθ呢？其实，我们所说的向量的加法、数乘、点乘的“定义”，更应该说是“公理”，类似于实数的运算1+1=2,2x2=4，都是从世界运行的规律中提炼出来，又反过来描述客观世界的真理，那么的准确、简洁、优美。

我们当然可以定义： a∙b=|a||b| sinθ，而且大学里学习抽象向量空间的知识后，会发现这个定义也能成立。但它并没有什么实际意义，它不能描述客观世界。

向先贤们致敬

最后，结合上面的理解，我们对教材中向量板块的知识点做一个梳理。

1.概念的引入

我们从一支笔，一棵树，一本书抽象出只有大小的数量“1”；

类似的，我们对力、位移、速度等既有大小又有方向的量进行抽象，形成一种新的量：向量。

2.运算的定义

包括向量加法、数乘和点乘。

不详细描述了，但我们再强调一次：这里所谓的“定义”更应该说是大量观察和试验之后总结出来的公理。

3.坐标表示

由向量的加法和数乘推导出了平面向量基本定理（平面中任意向量可以由另外两个不共线向量表达）

接着由平面基本定理推导出向量的坐标表示方法，从而给向量的运算提供了简洁的工具。

我们在这里也再次强调：引入向量和向量的运算的意义是为几何和物理研究提供强大、有力的工具；引入向量的坐标表示的意义是为了提供更简洁的工具。

所以，

但凡不能一眼看出如何求解的几何问题，就用向量方法；

但凡不能一眼看出如何求解的向量问题，就建立坐标系。

4.向量共线

向量共线是考试中特别喜欢考察的知识点，但因为有不同的表达形式，所以大家做题的时候容易搞不清楚，在这里写在一起，就比较容易理解和记忆了。